基于隨機理論的匯流影響因素分析
韓曉峰
(齊齊哈爾松嫩水利建筑工程有限責任公司,黑龍江齊齊哈爾161006)
水文模擬的理論基礎是產匯流理論。大量的實測資料表明,在產匯流過程中,存在著許多難以預測和控制的隨機性因素。概括起來主要表現在:①水文模型描述的降雨-徑流、河道洪水演算等過程都是建立在物理簡化的基礎上的,這就導致了模型結構的不確定性;②降雨時空分布和下墊面時空分布的不均勻性,以及水文資料或信息的不確定性等,導致了模型輸入的不確定性;③大多數水文模型的參數主要是依據降雨和徑流資料來率定,由于資料的選取、優化方法、目標函數及參數組合等因素而產生了模型參數的不確定性。這些不確定性因素始終存在并制約著防洪決策的正確性,目前廣泛采用的水文模型,認為其結構、模型的輸入及參數都是確定性的,即對于一個流域系統來說,認為系統響應是唯一的,這顯然是不符合實際情況的。針對自然界中存在的許多隨機不確定現象,用包含隨機元素的隨機微分方程建立和模擬其過程將更為優越。本文應用隨機微分方程對水文過程中的隨機不確定因素進行分析和探討。
1 理論依據
線性水庫的隨機匯流系統可表達為:
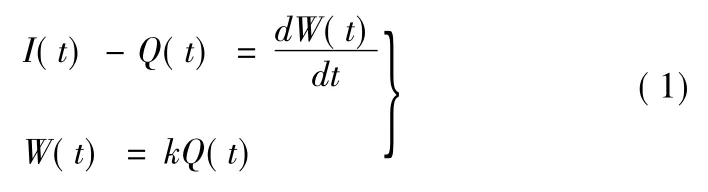
式中:I(t)為匯流系統的輸入;Q(t)為匯流系統的輸出;W(t)為匯流系統的蓄量;k為線性水庫的蓄量常數。圖1為線性水庫示意圖。
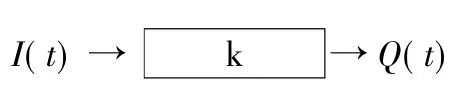
圖1 線性水庫示意圖
聯立上述兩式可得:
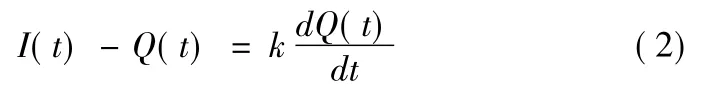
式(2)是匯流系統結構、參數及其輸入均為確定性時描述匯流過程的微分方程式。考慮匯流過程中的隨機不確定性,可進行如下處理:
1)線性水庫的隨機輸入過程。對于一個穩定的水文系統,有效降雨分布或河道上斷面流量在輸入時可考慮成一個隨機過程I(t),則在流域出口斷面形成相應的隨機出流過程Q(t)。考慮隨機輸入過程為馬爾可夫過程,可以認為,輸入的隨機過程是在其均值(t)的基礎上,疊加一個高斯白噪聲過程,即

式中: (t)為t時刻入流的均值;w(t)為t時刻輸入的高斯白噪聲過程,它具有零均值,且=w(t),B(t)為維納過程或布朗運動,屬于高斯隨機過程。
則式(2)可改寫為:
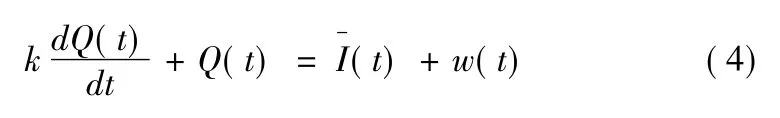
微分方程式(4)引入了輸入隨機項之后,即為具有隨機輸入項的隨機匯流模型,根據隨機微分方程理論,可解得出流過程的均值和方差為
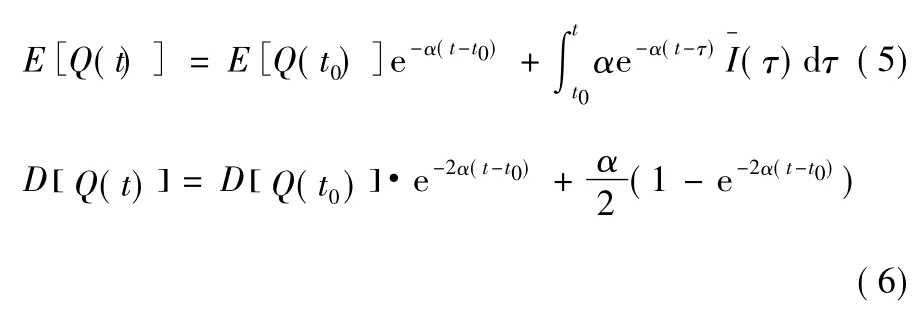
2)參數的隨機不確定性。匯流系統中包含的參數在傳統的匯流計算中,都是作為確定性值來考慮的。但是模型參數由于受眾多隨機性因素的影響,也具有一定的隨機性,各次洪水求出的模型參數可認為是其隨機性的具體表現。
根據定義,入流為單位函數時,其出流過程為S曲線。則根據式(2)可得S曲線的表達式為:

將式(7)中的參數α視為隨機變量,則根據隨機參數的隨機特性可確定隨機S曲線的統計特性,從而得到出流過程的各種統計特性。假定α服從正態分布,則有:
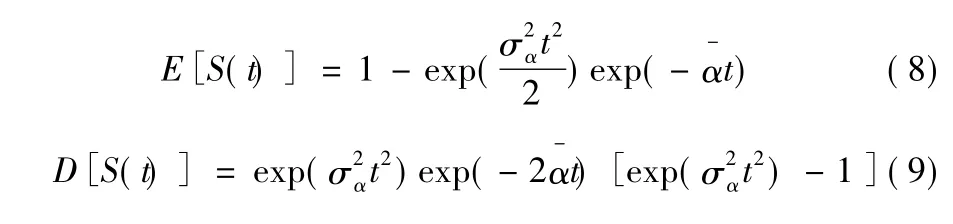
3)同時考慮輸入和參數均為隨機的情形。在方程式(4)中考慮參數k為隨機變量,則由隨機微分方程理論可知,式(4)是一個典型的It0方程,它具有隨機初始條件、隨機系數和隨機輸入項。這里采用建立矩方程來確定隨機出流過程的均值和方差。解得出流過程的一階原點矩和二階原點矩為:
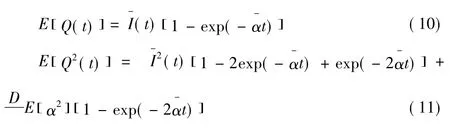
則方差可由D(Q(t))=E(Q2(t))-(E(Q(t)))2計算得到。
式中:D為入流過程強度;其它符號意義同前。
2 入流過程處理
在實際應用中,由于入流過程不是連續的函數形式,一般用離散數值的形式給出。因此,如果模型的入流過程可以分解成若干項之和,則總的入流過程所形成的出流過程必等于各分項入流過程所形成的出流過程之和。對于一個線性流域系統來說,我們可以把入流過程假設由一些簡單的基本函數組成,例如單位函數、脈沖函數等。這說明,欲求一般形狀的入流過程所形成的出口斷面流量過程,可首先求出簡單入流過程所形成的出流過程。
本文算例中模型輸入均值直接采用實測值,用單位入流函數給出其近似表達式如下:
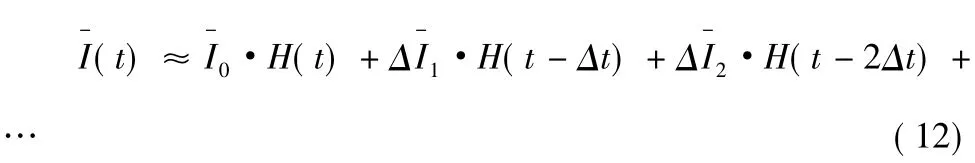
3 模擬結果分析與討論
針對上述3種情況,以湖南柘溪水電站下游江南~夫溪河段為例討論各種因素對匯流系統出流過程的影響。
湖南柘溪水電站下游江南~夫溪河段長L=20.1 km,波速為Ck=2.430~2.792 m/s,其入流資料見表1。試推求1967年5月13日~14日洪水的夫溪出流過程的均值和方差。
3.1 參數和初始值的確定
1)具有隨機輸入過程的情況。根據河段長L=20.1 km,波速為Ck=2.430~2.792 m/s,可得該河段的蓄量常數為k=2.3 h,取計算時段Δt=0.5 h。根據水文測驗規范規定的精度要求,假設輸入過程的變差系數約為0.05,即相對均方誤差為5%,初始出流過程為確定性量,即E[ Q (t0) ] =0,D[ Q (t0) ] =0。
2)參數為隨機變量的情況。蓄量系數均值取k=2.3 h,即α=0.435 h-1,變差系數為0.15,即蓄量系數的均方差為σα=0.0653 h-1。
3)參數和輸入均為隨機的情況。假定蓄量系數服從正態分布,即α~N(0.435,0.0019)。在河道洪水演算中,其輸入為上斷面的流量,誤差主要來源于測驗誤差,因此這里仍以實測流量作為均值過程,變差系數為0.1,并假定任一時刻的入流量服從實測值為均值,變差系數為0.1的正態分布。
3.2 結果分析
初始條件確定以后,根據式(5)和式(6)計算具有隨機輸入的出流過程的均值和方差,根據式(8)和式(9)計算具有隨機參數的出流過程的均值和方差,根據式(10)和式(11)計算參數和輸入均為隨機的出流過程的均值和方差,具體計算結果見表1。
表1給出了各種隨機性因素影響下的江南-夫溪河段一次洪水出流過程的均值和均方差。從表1數據可以看出,3種情況下計算得到的均值過程相差不大,這主要是因為本次采用的模型為一個線性水庫模型,其蓄量調節能力稍差,但對于給河段的計算滿足精度要求。從計算得到的均方差過程可以看出,輸入隨機不確定性對預報的影響大于參數隨機不確定性對預報的影響。這是因為對于具有隨機系數的出流過程的方差主要取決于蓄量系數的變差系數,本次計算中,江南-夫溪河段隨機參數的變差系數為0.15,而參數和輸入均為隨機時的變差系數為0.1,導致隨機參數情況下計算的均方差偏大,這說明預報的不確定性增大了,因此,隨機蓄量系數的變化大小直接影響著洪水出流過程的不確定性程度。
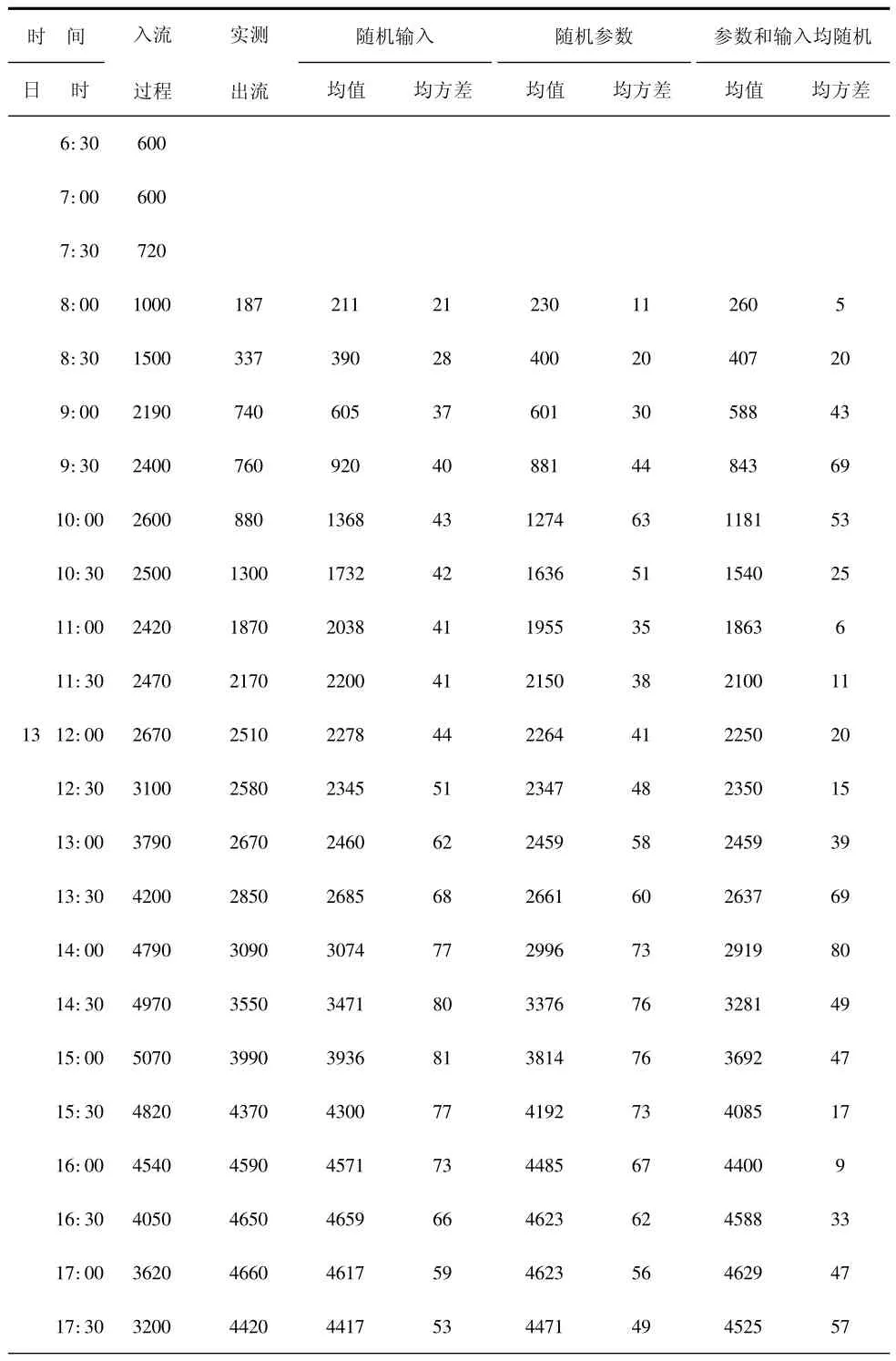
表1 江南-夫溪河段出流過程模擬計算成果表 m3/s
4 結論
1)考慮各種隨機性因素對匯流系統出流過程的影響,可以同時給出匯流系統出流過程的均值及均方差過程,從而確定各種需要的出流過程的統計特性,為防洪決策提供依據。結果表明,具有隨機系數的出流過程的方差主要取決于蓄量系數的變差系數,隨機蓄量系數的變化大小直接影響著洪水出流過程的不確定性程度。
2)考慮各種不確定性對出流過程的影響,可以為防洪決策、降低風險提供了有價值的不確定度。考慮隨機性因素的影響建立的匯流模型,得到的出流過程不再是一個確定性的數值,而是服從某種分布的概率形式。這對進行洪水的概率預報等會有所幫助。
3)本文僅以線性水庫為例,分析探討了影響匯流過程的隨機不確定性因素,對于更復雜的流域匯流系統還有待于進一步深入研究。
[1]芮孝芳.水文學原理[M].北京:中國水利水電出版社.2004.
[2]孫穎娜,王紅星,惠琳.流域匯流系統隨機不確定性分析[J].黑龍江大學工程學報,2011,2(2):16-18.
[3]Krzysztofowicz,R.,Maranzano,C.J.Bayesian system for probabilistic stage transition forecasting[J].Journal of Hydrology,2004(299):15-44.
[4]趙仁俊.流域水文模型的比較分析研究[J].水文,1989(6):1-5.
[5]謝平,胡彩霞,譚瑩瑩,等.西江歸槽洪水研究進展[J].黑龍江大學工程學報,2011,2(1):29 -33.
[6]任立良,劉和遠,袁飛.水文學演進歷程的特征剖析[J].黑龍江大學工程學報,2011,2(1):24 -28.
[7]郭生練,李蘭,曾光明.氣候變化對水文水資源系統影響評價的不確定性分析[J].水文,1995(6):8-14.
[8]張洪剛,郭生練,何新林,等.水文預報不確定性的研究進展與展望[J].石河子大學學報(自然科學版),2006,24(1):15-21.
[9]孫穎娜,芮孝芳.隨機輸入情況下匯流計算方法的探討[J].水科學進展.2005,16(5):661-665.

