模糊神經網絡PID在恒氣體流量控制中的應用
杜魯濱張存
(1.新能鳳凰(滕州)能源有限公司,山東 滕州 277527;2.太原理工大學,太原 030024)
氣流量控制在工業領域是個常見系統,但是該系統較復雜,它與流量變送器信號、流體密度、相對濕度、壓力和溫度等因素有關。氣體恒流量采用典型的閉環控制系統來實現的,控制方案通常采用傳統的比例積分微分調節器,但其三個控制參數Kp、Ki、Kd一般是人工整定,有一定的局限性,不能在線實時調整[1],已無法滿足控制的要求,此時在近幾年迅速發展的模糊控制(Fuzzy)和神經網絡(Neural Network)無疑映入我們的腦海。常規PID、模糊控制及神經網絡三種控制作用的優缺點如表1所示。
從表1可知,常規PID、模糊控制(Fuzzy)及神經網絡(Neural Network)三種控制算法都有各自的優缺點,鑒于此本文將PID、模糊和神經網絡三種控制技術的優點相結合,用神經網絡來構造模糊系統,即利用神經網絡的學習方法來調整模糊系統的參數,揚長避短使控制效果大幅提高。本文采用模糊RBF神經網絡在線實時整定PID控制器的三個參數Kp、Ki、Kd,從而實現對氣體流量的實時監控。

表1 三種PID控制算法的優缺點
1 模糊神經網絡控制器的結構和原理
RBF模糊神經網絡(FuzzyRBFNN)的結構如圖1所示。該網絡由輸入層、模糊化層、模糊推理層及輸出層構成。第一層為輸入層,第二、第三層為隱含層,第四層為輸出層[2]。
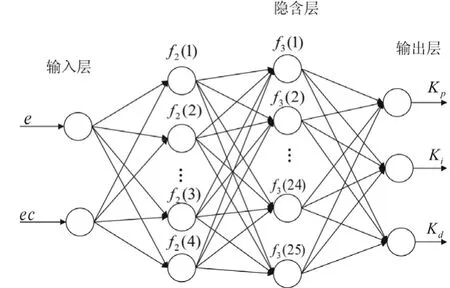
圖1 Fuzzy RBFNN的結構
FuzzyRBFNN有兩個的輸入節點,分別為標準氣流量的偏差e和偏差變化率ec。本文偏差e和偏差變化率ec模糊量的量化等級選為5級,具體定義如下:
e的論域為:[-2,2]
ec的論域為:[-2,2]
e的模糊語言值為:{NB,NS,ZO,PS,PB}
ec的模糊語言值為:{NB,NS,ZO,PS,PB}[4]
由此可以確定Fuzzy RBFNN第二層的節點數為L=5,第三層的節點數為N=5×5=25。Fuzzy RBFNN的輸出層節點數為3,分別為PID控制器的Kp、Ki、Kd三個參數。
第一層:輸入層。
輸入節點個數也是輸入變量個數,輸入層(第一層)的各節點直接與輸入量的各分量相連接,把輸入量傳遞到下一層。第一層的每個節點i的輸入輸出關系可表示為
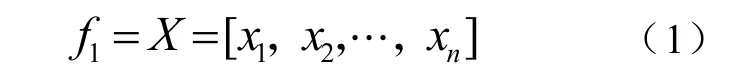
第二層為隸屬度函數層。
本層的功能主要是模糊化輸入變量,各輸入變量模糊子集數的和就為本層節點的個數,每個節點就代表一個語言變量值,其主要作用是計算每個輸入分量屬于各語言變量值模糊集合的隸屬度函數,本文采用高斯函數作為隸屬函數,cij和σij分別是第i個變量第j個模糊集合的隸屬函數的中心和寬度[2]。

第三層:模糊推理層。
把模糊推理層和模糊化層(即第二層和第三層)連接起來,實現模糊規則的匹配及各節點間的模糊運算,根據Fuzzy系統的推理方式(if A And B then C),確定Fuzzy RBFNN的模糊推理層的個數為5×5=25個,也就是系統中49條Fuzzy規則前件。本層每個節點的輸出(每條規則的適用度)是該節點所有輸入信號的乘積[4],即
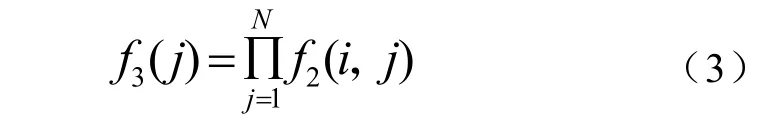
第四層:輸出層。
本層采用加權平均的方法來反模糊化,可清晰準確的計算出輸出參數,從模糊化層(第三層)到輸出層(第四層)的初始權值是影響控制器輸出的關鍵因素。Kp、Ki、Kd是模糊RBF神經網絡PID控制器的輸出層的三個節點輸出。

式中,wij組成輸出節點與第三層各節點的連接權矩陣i=1,2 3,。即
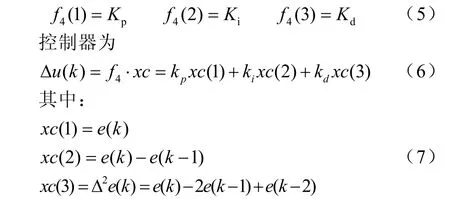
采用增量式PID控制算法:

采用Delta學習規則來調整參數,定義目標函數為
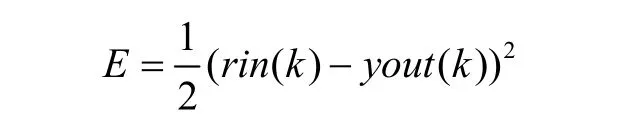
式中,rin(k)為網絡理想輸出;yout(k)為網絡實際輸出;rin(k)-yout(k)為每一個迭代步驟k的控制誤差。網絡權值的學習算法為

式中,Wj為網絡輸出節點和上一層節點的連接權,j =1,2,…,N,η為學習效率。
如果考慮動量因子,則輸出層權值為

式中,k為網絡的迭代步驟,α為學習動量因子[2]。
2 模糊神經網絡控制器的設計步驟
該控制器控制算法步驟歸納如下:
1)確定Fuzzy RBF神經網絡輸入層節點數、隱含層節點數及輸出節點數,設定各層的加權初始值,選定學習速率η及動量因子α,此刻k=1。
2)采樣得到rin(k)和yout(k),計算該時刻誤差error= rin(k)-yout(k)。
3)計算神經網絡各層神經元的輸入、輸出,輸出層輸出即為PID控制器的三個可調參數Kp、Ki、Kd。4)采用經典增量式數字PID的控制算法:
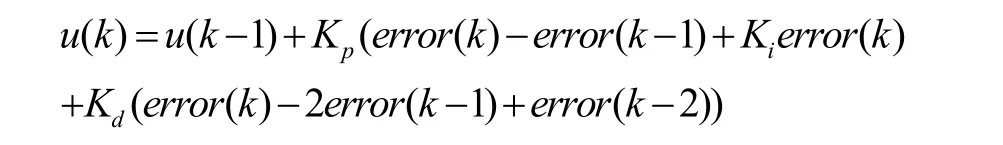
計算PID控制器的輸出u(k)。
5)神經網絡學習訓練,在線實時調整加權系數,實現PID的三個控制參數的自適應調整。
6)最后判斷精度是否滿足要求,如果不滿足置k=k+1,返回到(1)循環執行,否則程序運行結束[5]。
3 仿真分析
在Matlab軟件M文件的編程環境下進行仿真,網絡學習速率η=0.20,學習動量因子α=0.02,加權系數初始值取區間[-2.0,2.0]上的隨機數,采樣周期Ts=4s,當輸入信號為單位階躍信號(rin(k)=1.0)時,采用M語言進行仿真得到系統的響應曲線如圖2所示。
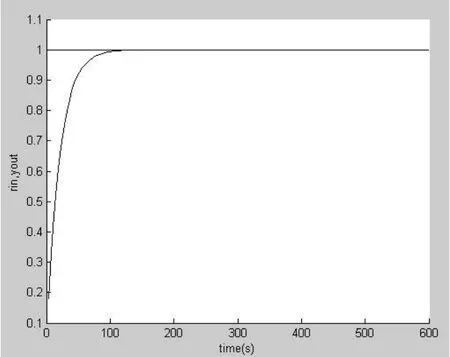
圖2 模糊RBF-PID算法的階躍響應曲線
本文還需設計傳統PID、模糊PID、RBF神經網絡PID三種控制器,以便于與模糊RBF神經網絡PID控制器的性能相比較。在M文件的編程環境下,四種控制算法的階躍響應曲線如圖3所示。其中,1為常規PID的階躍響應曲線;2為模糊PID的階躍響應曲線;3為RBF神經網絡PID的階躍響應曲線;4為模糊RBF神經網絡PID的階躍響應曲線。
為了比較四種控制方案的抗干擾能力情況,在k=100,即T=400s時刻加一干擾信號 ξ(100) =0.1,此時四種控制算法的響應曲線如圖4所示。其中,1為常規PID的響應曲線;2為模糊PID的響應曲線;3為RBF神經網絡PID的響應曲線;4為模糊RBF神經網絡PID的響應曲線。

圖3 常規PID、Fuzzy-PID、RBFNN-PID、Fuzzy RBFNN-PID無干擾時的階躍響應曲線

圖4 常規PID、Fuzzy-PID、RBFNN-PID、Fuzzy RBFNN-PID有干擾時的階躍響應曲線
通過比較上圖四種控制算法響應曲線的調節時間Ts(s)、超調量σp(%)及穩態余差e(∞)(%)可知:Fuzzy RBFNN-PID的控制性能要明顯地優于其他幾種控制方式,該控制系統調節時間快,超調量小,抗干擾性強,適應性好。通過仿真分析表明Fuzzy RBFNN-PID控制的可行性及優越性,針對氣體恒流量控制系統的特點,采用Fuzzy RBFNN-PID參數自整定控制氣體流量將會起到很好的效果。
[1]董春宵,趙元黎,張永利等.Fuzzy-PID算法在氣體流量控制中的應用[J].微計算機信息,2008(25):31-33.
[2]劉曉丹.基于RBF模糊神經網絡的船用鍋爐汽包水位控制研究[D].大連大連海事大學,2008.
[3]吳文貢,應科煒,湯達斌等.基于單片機的流量控制系統[J].儀表技術,2006, (3):25-26.
[4]黃運生,張少華,陳學.還原氣體流量的模糊自適應PID控制[J].電氣傳動,2009,39(8):48-51.
[5]飛思科技產品研發中心.Matlab 7輔助控制系統實際與仿真[M].北京:電子工業出版社,2005:7-61.

