MathCAD在連接體問題研究中的應用
——再議連接體中物體最大速度問題

姜付錦

（武漢市黃陂區第一中學 湖北 武漢 430030）

文獻［1］～［3］都是討論連接體中物體最大速度問題；其中文獻［1］準確、精煉地研究了這個問題并且利用幾何畫板求得一個物體最大速度的位置，但是沒有求出兩個物體的最大速度及另一個物體取最大速度的位置；文獻［2］與文獻［3］非常系統和完整地研究了這個問題中的加速度關系及兩個物體在取最大速度時的位置并且得到了最大速度的表達式，但計算過程非常簡單不直觀、具體；文獻［2］不僅得到兩物體達到最大速度時的位置而且還通過理論證明了在此位置有最大速度的原因，但是文中的公式和描述性語言過多不便于讀者深刻領會.現筆者通過MathCAD來研究此問題，如果文中有不當之處，請各位物理同仁批評指正.

MathCAD是美國Mathsoft公司推出的一個交互式數學軟件，該軟件定位于向廣大教師、學生、工程人員提供一個兼備文字、數學和圖形處理能力的集成工作環境，使他們能方便地準備教案，完成作業或準備科學分析報告.在輸入一個數學公式、方程組、矩陣之后，計算機能直接給出結果，而無需考慮中間計算過程.在計算機中輸入數學公式、符號和等式，可以很容易地算出代數、微積分、三角函數以及很多科技領域中的復雜表達式的值，并可顯示數學表格和圖形，通過對圖形結果的分析，使對問題的理解更加形象.

1 題目1

如圖1所示，一輕繩通過無摩擦的定滑輪，一端與放在傾角為α＝30°的光滑斜面上的質量為m1的物體A相連，另一端與套在光滑豎直桿上質量為m2的物體B相連.定滑輪M到豎直桿的距離為l＝m，桿上N點與定滑輪的高度相同，當物體B在距N點下方1m處時，A和B恰好靜止，求

（1）物體A和B的質量之比；

（2）將物體B從N點由靜止開始釋放，物體B下滑過程中的最大速度大小.

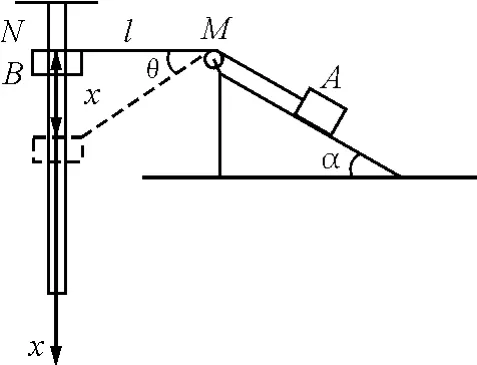
圖1

1.1 分析

第一問的結果為＝4.以物體B出發點為原點豎直向下為正方向建立x軸，設某一時刻物體B下降位移為x，則物體A沿斜面移動距離為y＝.設繩子的拉力大小為F，與水平方向成θ角，則有以下微分方程組

初始值為

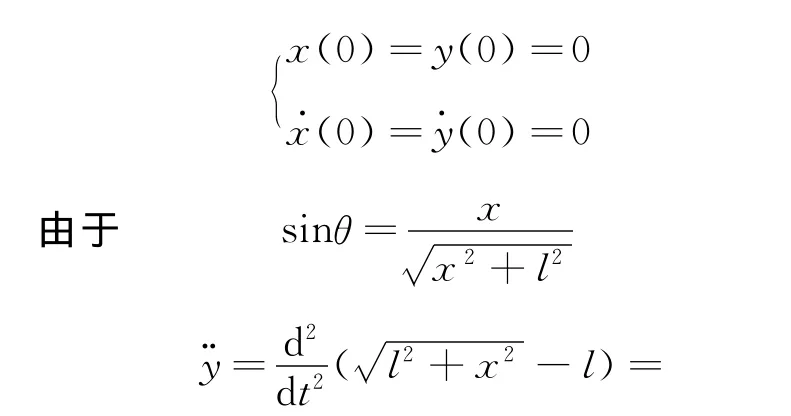
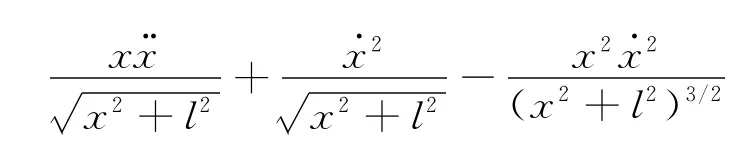
所以上式可化為

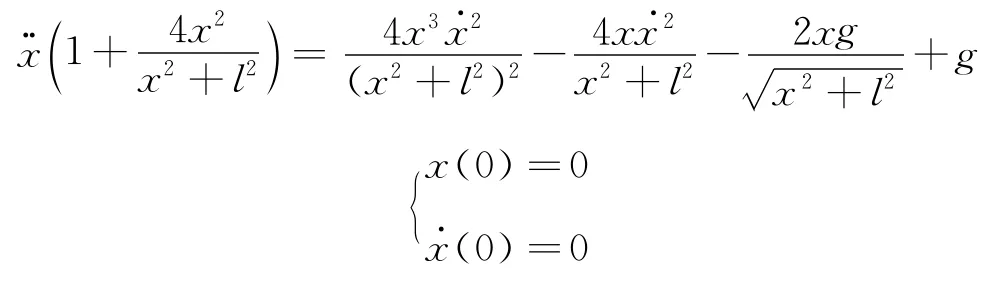
1.2 利用MathCAD解微分方程

利用MathCAD解微分方程，如圖2所示.

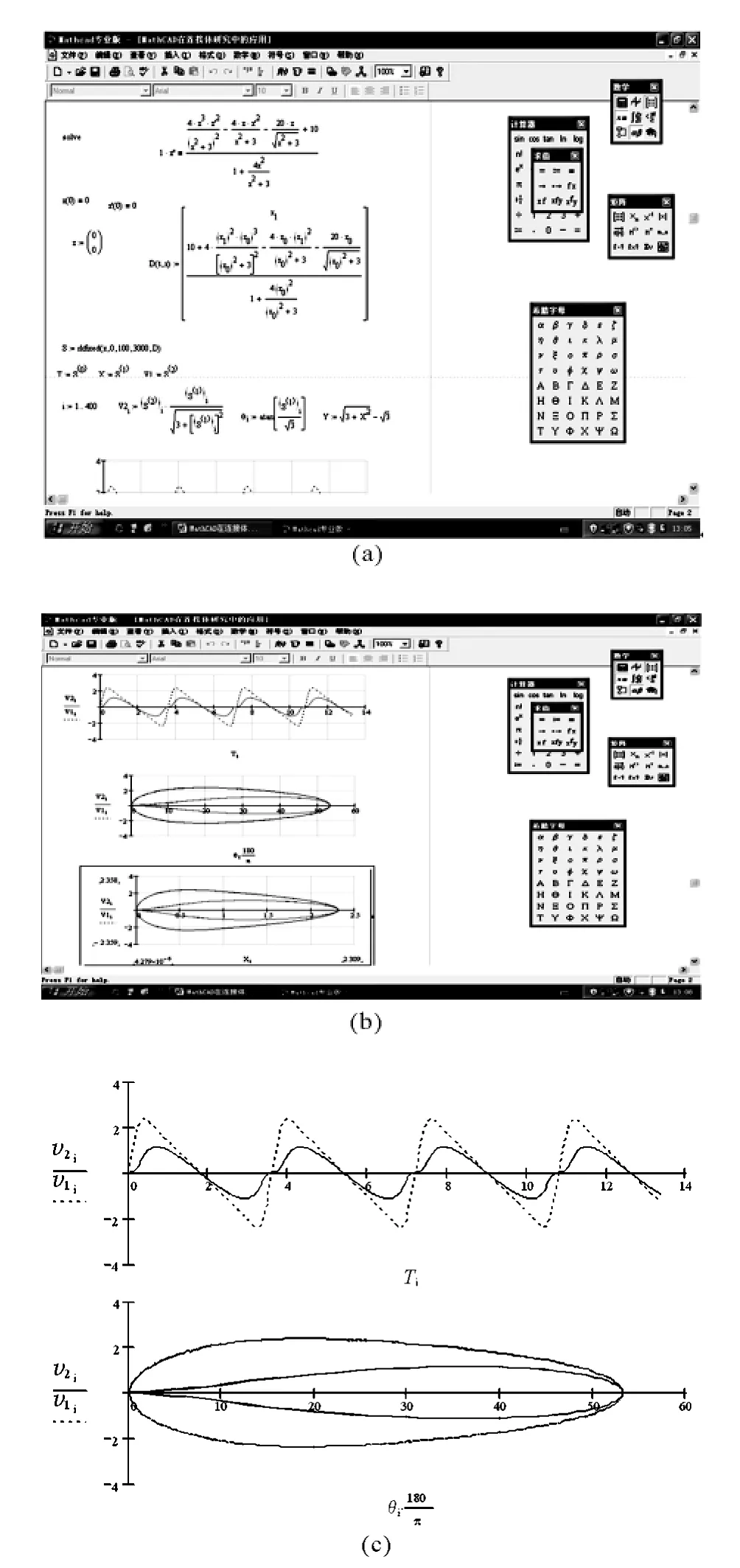
圖2

1.3 圖形分析

在圖2（c）中v1i，v2i分別表示B物體與A物體的速度，Ti表示物體運動的時間，表示繩子與水平方向的夾角.由圖可知，兩物體的運動都是周期性的，周期是3.6s.當θ＝20.01°，即t＝0.4s時，B物體第一次達到最大速度2.358m／s；當θ＝36.452°，即t＝0.7s時，A物體第一次達到最大速度1.130 8m／s；兩物體達到最大速度時的位置與時間都不同.這與文獻［1］和文獻［3］中的結論是一致的.

2 題目2

如圖3所示，一段足夠長輕繩跨過兩個等大等高的定滑輪后，兩端各有一個質量為m的物體A和B，系統開始處于靜止狀態.此時，在繩子的中點掛一個質量也為m的物體C，已知兩定滑輪的間距為2L，忽略滑輪的摩擦力和空氣阻力，設重力加速度為g.試分析物體C在什么位置取最大速度及最大速度為多少？

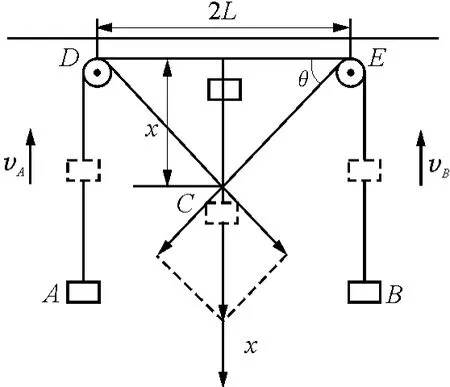
圖3

2.1 通常分析

當DC，EC夾角為120°時，系統處于平衡狀態，物體C有最大速度，設最大速度為vm.由運動的合成與分解知識可知物體A，B的速度為vmcos 60°，設物體C下降的高度為h，則有h＝；物體A，B上升的高度為.由系統機械能守恒定律可知

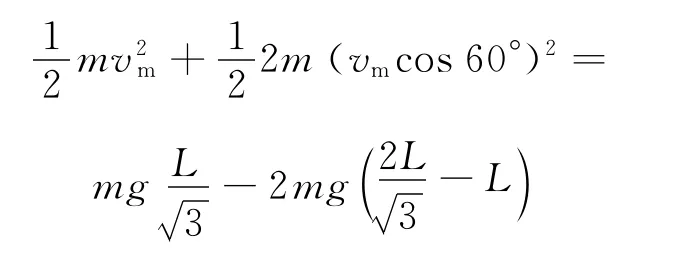
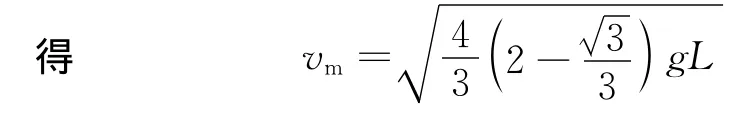
2.2 正確分析

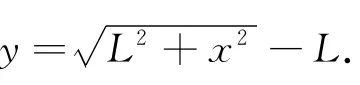
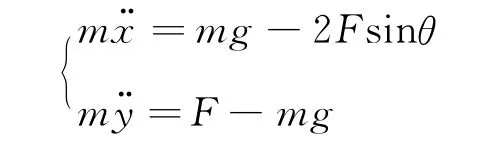
初始值為

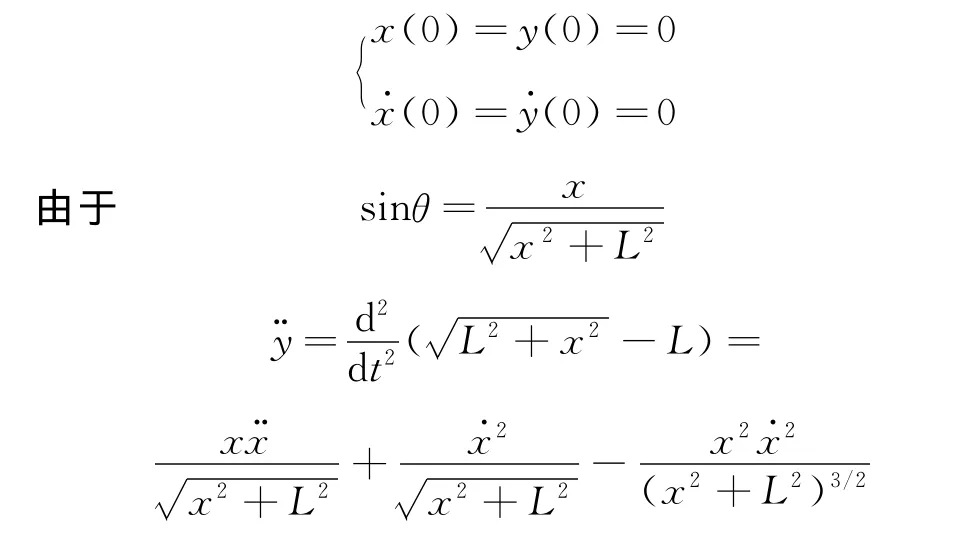
所以上式可化為

2.3 利用MathCAD解這個微分方程

用MathCAD解該方程，如圖4所示.

圖4

2.4 圖形分析

設三個物體的質量均為m＝1kg，重力加速度g＝10m／s2，兩定滑輪的間距2L＝20m，v1i，v2i分別為物體C和物體A（B）的速度，Ti，分別為時間及繩子與水平方向的夾角.由圖4（c）可知，當時間為1.033 3s時，物體C第一次達到最大速度vm＝6.211m／s，繩子與水平方向的夾角為22.921°；當時間為1.633 3s時，物體A（B）第一次達到最大速度3.238 6m／s，繩子與水平向上方向的夾角為38.038°；三個物體運動的周期為7.433s.這與文獻［2］中的結論是一致的.

從以上的應用可以發現MathCAD具有強大的數學運算功能，利用它可以進行復雜的理論計算和創作設計物理教學與研究，也可以用來精確模擬各種物理現象，把物理概念、物理方程及其解答有機結合起來，達到“形象思維與抽象思維的統一”.用MathCAD研究物理問題，效率很高，操作簡便，避開了復雜、重復、容易出錯的數學計算和耗費精力的計算機編程，把精力和智慧集中在物理問題的本質部分.運用它可以在計算機上開展實驗，尤如“在智力游戲的同時，探索極其復雜的原理”.這里既有數學和物理，也有藝術.

1 何征宇.用“幾何畫板”的函數功能研究物理疑難問題.物理通報，2010（4）：65～66

2 孫林燕，黃振平.輕繩連接體中的加速度問題.物理通報，2010（5）：70～71

3 易行.談談充分發揮習題的“物理營養”.物理通報，2010（6）：56～58