攝像機標定算法研究
謝莉余勝
(湖南人文科技學院物理與信息工程系 湖南 婁底 417000)
0 引言
由攝像機拍攝的圖像信息出發計算三維物體的幾何信息,實現物體的三維結構重建是計算機視覺的基本任務之一[1]。攝像機標定是指建立空間物體表面某點三維幾何位置與圖像中對應點位置之間的關系。攝像機標定問題涉及到兩組參數:用于剛體變換時,相對于世界坐標系的攝像機坐標的三維位置和方向的外部參數;攝像機自身所擁有的內部參數是指攝像機的內部光學和幾何特性,包括圖像中心、焦距、鏡頭畸變等。
1 攝像機模型和成像原理
1.1 圖像坐標系
通過攝像機獲取的圖像在計算機中是以數組形式存儲,數組中的每個元素(像素)值稱為圖像點的亮度。如圖1所示,在圖像中定義坐標系u-v,每一個像素點均有唯一坐標u-v來表示像素所在的行數和列數。即u-v是以像素為單位的圖像坐標系坐標。由于直角坐標系u-v只表示了數字圖像中像素所處的行數和列數,而沒有用物理單位表示出該像素在圖像中的位置。因此,需要再建立以物理單位(如毫米)表示的坐標系x-y,(x,y)表示以毫米為單位的圖像坐標系的坐標。
在x-y坐標系中,原點O1定義在攝像機光軸與圖像平面的交點處,稱為圖像平面的主點(principal point),理論上它應在圖像的中心位置,但是由于制作工藝方面的原因,一般也會有些偏差。設O1在u-v坐標系中的坐標為(u0,v0),每一個像素在x軸和y軸方向上的物理尺寸大小為dx,dy,則在圖像中每一個像素在兩個坐標系下的坐標有以下關系:
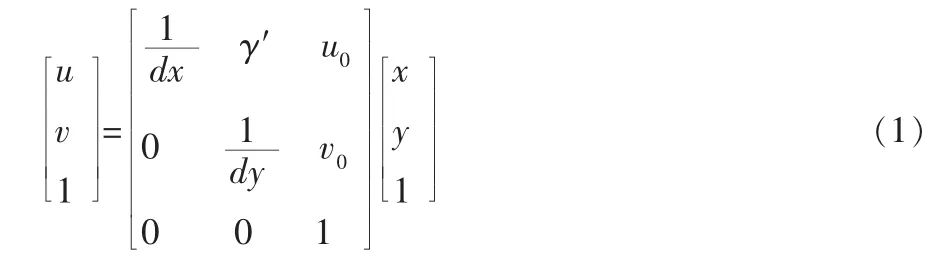
其中γ′為斜度因子,表示u軸和v軸的不垂直程度。理想情況下u軸和v軸相互垂直,即γ′等于0。
1.2 攝像機坐標系
圖2所示為攝像機成像的幾何關系。其中點O稱為攝像機光心,Xc軸和Yc軸分別與圖像的x軸與y軸平行,Zc軸為攝像機的光軸,它與成像平面垂直。光軸和圖像平面的交點,即為圖像坐標系的原點。由光心O與Xc,Yc和Zc軸組成的坐標系稱為攝像機坐標系。攝像機焦距為OO1。
1.3 世界坐標系
在我們所處的真實環境中,還需選擇一個參考坐標系來描述三維空間中物體之間的位置關系,稱之為世界坐標系。攝像機坐標系和世界坐標系可以通過旋轉矩陣R和平移向量t來描述,空間點A在世界坐標系與攝像機坐標系下的齊次坐標分別為:(Xw,Yw,Zw,1)T、(Xc,Yc,Zc,1)T,那么將有如下關系:
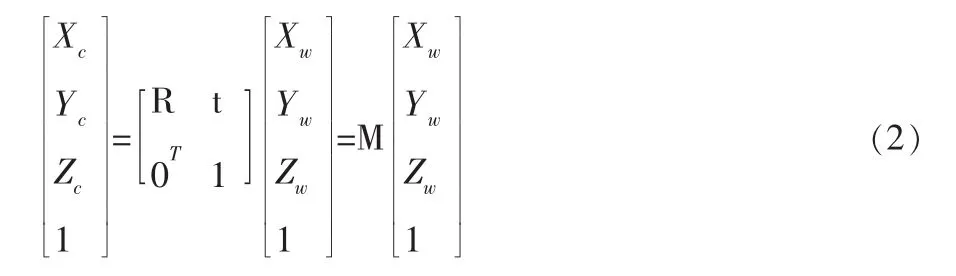
其中,R為 3×3正交旋轉矩陣;t為三維平移向量;0=(0,0,0)T;M 是 4×4 矩陣,為兩個坐標系之間的變換矩陣。
1.4 針孔攝像機模型
在計算機視覺中,場景中的空間點與其在圖像中的成像點之間的相互關系,是由攝像機成像幾何模型來確定的。
針孔模型的物理意義相當于薄透鏡成像,該模型最大的優點是成像關系是線性的。它簡單實用,其準確度高,在計算機視覺中廣泛使用。如圖2所示,三維空間中任意一點A在圖像上的成像位置可用針孔模型來近似表示,即圖像點a是空間點A和光心O的連線與成像平面的交點。由比例關系有如下關系式:

其中,(x,y)是 a 點的圖像坐標,(Xc,Yc,Zc)為空間點 A在攝像機坐標系中的坐標。用齊次坐標與矩陣可表示為:
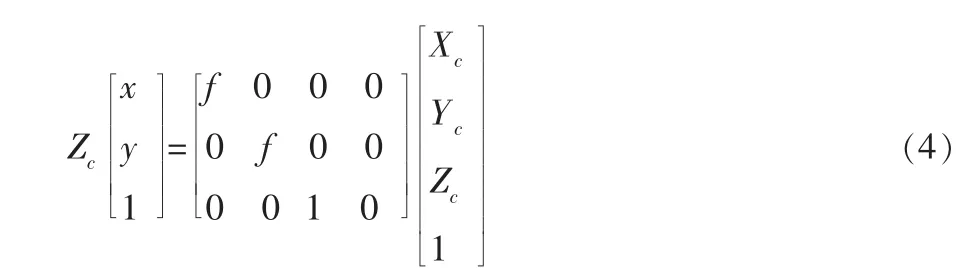
把式(1)、(2)代入式(4)中,可以得到圖像坐標與世界坐標之間的關系:
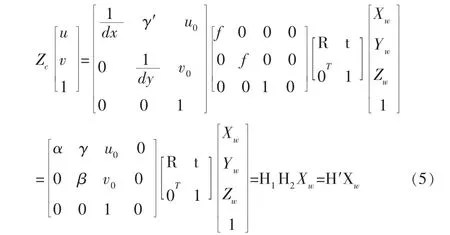
其中,α=f/dx,β=f/dy,γ=γ′f;H′是 3×4 矩陣, 稱為投影矩陣; H1僅由 α,β,γ,u0,v0決定,因為 α,β,γ,u0,v0僅與攝像機內部結構有關系,所以稱這些參數為攝像機內部參數;H2僅由攝像機相對于世界坐標系的方位決定,稱為攝像機外部參數。
由此可知,攝像機標定的過程也就是求解攝像機外部參數和內部參數的過程。
2 兩種攝像機標定算法
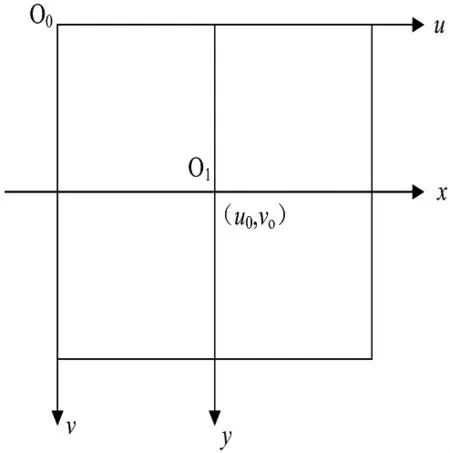
圖1 圖像坐標系
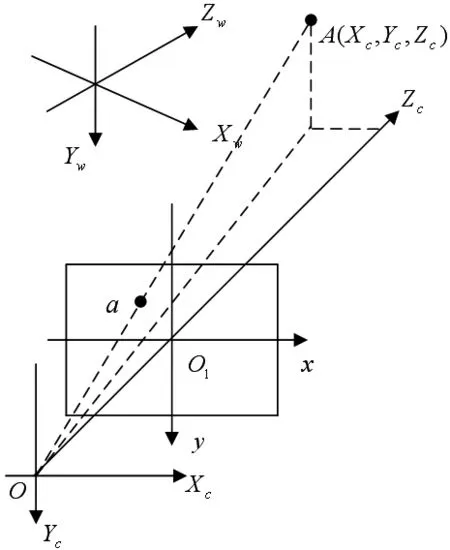
圖2 圖像坐標系與世界坐標系

圖3 標定圖像圖
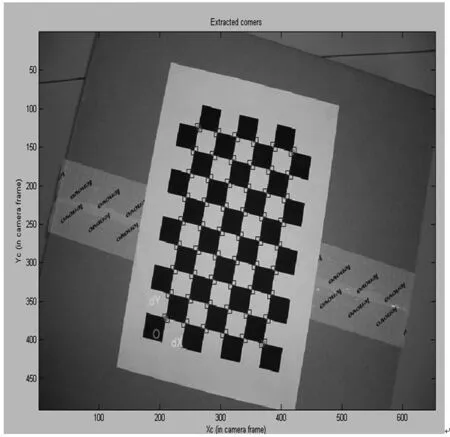
圖4 角點提取
2.1 Tsai兩步法
Tsail[2]提出用兩步法對攝像機進行標定,首先利用直接線性變換方法或者透視變換矩陣方法求解攝像機參數,再用求得的參數作為初始值,考慮徑向畸變因素,并利用最優化算法進一步提高標定精度。在其標定算法中,CCD陣列中感光元的縱向和橫向間距假定是己知的,具體數值由攝像機廠家提供。所假設的內、外部參數分別是:(1)f等效焦距;(2)k鏡頭畸變參數;(3)Sx非確定性尺度因子,它是由攝像機橫向掃描與采樣定時誤差引起的;(4)(cx,cy)圖像中心或主點;(5)R,T 三維空間坐標系與攝像機坐標系之問的旋轉矩陣和平移向量。但Tsai兩步法只考慮了徑向畸變,沒有考慮切向畸變,這與實際情況有較大的偏離,限制了標定精度的進一步提高。
2.2 張正友標定算法
由于傳統標定方法需要價格昂貴的高精度標定設備,張正友在1999年提取了一種簡單、靈活、實用的攝像機標定方法[3]。該方法只需要攝像機對一標定板在不同方向進行拍照,攝像機與標定板間可以自由地移動,運動的參數無需已知,對每個視點獲得圖像,提取圖像上網格的角點;標定板與圖像的網格角點對應關系,確定了單應性矩陣,對每幅圖像,就可確定一個單應性矩陣,這樣就能夠進行攝像機定標。該算法先有一個線性解法,然后基于極大似然準則對線性結果進行非線性優化求精,而標定板的運動方式不必知道。通過對2D信息的提取計算來得到最終的結果。
3 實驗結果
本文所標定相機型號為三星S860,選用7×10棋盤格式的標定紙,每一方格的寬度為23mm,用相機從不同角度獲取12幅圖像(653×490)。本文采用文獻[4]提供的MATLAB工具箱實現張正友標定算法。圖3顯示了拍攝的12幅棋盤圖像,圖4為其中一幅標定圖像的角點提取情況。
實驗結果所得到的攝像機內部參數為:焦距:[219.06267,229.50868],主點:[326.00000,244.50000]。
畸變:[-1.94496,1.04910,-0.03290,-0.20754,0.00000]±[0.49090,2.75113,0.01008,0.09371,0.00000]。
斜度因子:0。
4 結論
本文分析了攝像機的模型和成像原理,對比分析了張正友標定方法和Tsai兩步法的標定原理。通過MATLAB工具箱所做標定實驗驗證了張正友標定法是一種簡單、易于實現的且有較高精度的攝像機標定方法。
[1]Yong J Y,Qi D Z.Camera Calibration in Binocular Stereo Vision of Moving Robot[C].The sixth world congress on intelligent control and automation,Dalian,China,2006:9257-9621.
[2]Tsai R Y.A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-the-shelf TV camera and lenses[J].IEEE journal of robotics and automation,1987,3(4):323-344.
[3]Zhang Z Y.A flexible new technique for camera calibration[J].IEEE transactions on pattern analysis and machine intelligence,2000,22(11):1330-1334.
[4]Jean Y B.Camera Calibration Toolbox for Matlab [EB/OL].[2009-12-28] (2008-6-2).http://www.vision.caltech.edu/bouguetj/calib_doc/index.html#examples.

