基于多類迭代局部搜索的自動化排課算法

宋婷 陳矛 吳超 張龔釗

摘 要：針對局部搜索算法容易陷入局部最優，無法自適應多種約束條件下排課的問題，提出一種基于多類迭代局部搜索的自動化排課算法。首先，通過多類分類器依據排課問題特征對排課問題進行分類，指導迭代局部搜索的鄰域選擇及參數設置。然后，在迭代局部搜索的過程中，使用基于序列的貪婪算法獲得可行解。最后，采用以問題特性為導向的雙溫控制模擬退火算法在鄰域中搜索局部最優解，并通過特定的擾動策略對當前最優解進行擾動后作為新的初始解進行迭代，最終達到全局最優。該算法在兩個國際著名的數據集，即第二屆國際時間表大賽基于課程的時間表數據集和Lewis 60數據集上進行了測試。實驗結果表明，與當前文獻中求解該問題的其他性能較優算法相比，所提出的算法具有更高的求解效率和質量。

關鍵詞：自動化排課;多類;迭代局部搜索;模擬退火;最優化

中圖分類號：TP301.6（算法理論）

文獻標志碼：A

Abstract： Focusing on the issue that local search algorithm is prone to fall into the local optimum and does not adapt to the course arrangement under multiple constraints， an automated course arrangement algorithm based on multi-class iterated local search was proposed. Firstly， the course arrangement problems were classified by the multi-class classifier according to the characteristics of the problems to guide the neighborhood selection and parameter setting of the iteration local search. Then， in the process of iterated local search， the sequence-based greedy algorithm was used to obtain the feasible solutions. Finally， the problem characteristics oriented two-temperature control simulated annealing algorithm was used to search for local optimal solution in the neighborhood and the current optimal solution was perturbed by a specific strategy and iterated as the new initial solution to achieve global optimization. The proposed algorithm was tested on two internationally famous datasets， which are the second international timetabling competition dataset and Lewis 60 dataset. The experimental results show that， compared with the existing efficient algorithms in current literatures， the proposed algorithm has higher efficiency and solution quality.

Key words： automated course arrangement; multi-class; Iterated Local Search （ILS）; Simulated Annealing （SA）; optimization

0 引言

自動排課問題是一個包含教室、課程、時間、班級、教學資源等多種因素的組合優化問題，已被證明是一個非確定多項式（Non-deterministic Polynomial， NP）完全問題[1]。由于該類問題的復雜性，引起了越來越多學者的關注和研究。2002年，英國和意大利合作組織了五年一屆的國際時間表競賽（International Timetabling Competition，? ITC）[2]，旨在為研究者提供一個可以普遍接受的基準來縮小研究與實踐之間的差距。排課問題通常被定義為在特定約束條件下，盡可能合理地安排有限的教育資源。其約束可被分為兩類：在任何情況下都不能違反的約束稱為硬約束;而那些可以違反，但應盡可能地減少違反值的約束被稱為軟約束。滿足了所有硬約束的課程表被稱為可行解，而最優的課程表（最優解）則是指在滿足所有硬約束的條件下，最小化軟約束的違反值。

對于這類NP難問題，確定型算法只適用于在合理的時間內解決小規模問題實例。因此，ITC競賽及其后大多數的相關研究都集中在快速近似啟發式算法和元啟發式算法上，以尋求在給定的時間范圍內獲取可行的最優解決方案。典型的算法有基于圖著色的方法[3]、模擬退火（Simulated Annealing， SA）算法[4]、禁忌搜索算法[5]、變鄰域搜索算法[6]、遺傳算法[7]、蟻群算法[8]、蜂群算法[9]、和聲搜索算法[10]等。但所有方法都還未能達到所給定問題解的下界，對問題最優解的進一步探討仍在進行。在這些算法中，雖然模擬退火（SA）算法是一個簡單且易于實現的通用框架，但它對于排課這類組合優化問題的求解確實非常有效。例如，第一屆國際時間表競賽的冠軍和第二屆國際時間表競賽的三個類別組的冠軍均采用了基于SA的算法。

解決排課問題的算法通常由兩階段組成：首先構建一個可行的排課方案，然后盡可能地減少軟約束違反值。通常，時間表問題可以等同于一個圖著色問題，對于大多數ITC競賽的排課問題實例而言，獲得可行的排課方案幾乎不能構成挑戰。 因此參賽算法的主要焦點都集中在最小化軟約束違反值上。

近年來，Lewis等[11]創建了一組60個僅包含硬約束的測試數據集，其創建目的在于將注意力聚焦于尋求可行解，以對不同算法進行更公平的比較。而傳統基于序列的技術只能為一小部分測試實例找到可行解。針對該問題，已經有多種不同的算法提出來求取這些測試實例的可行解。包括混合模擬退火算法[12]、基于團的算法[13]、基于事件插入的啟發式算法[14]、基于模擬退火的元啟發式算法[15]、memetic算法[16]等。迄今為止，這些方法依然無法完全解決所有樣本。因此，Lewis等[11]的這組測試實例，直到今天仍然是評估不同方法的一個具有挑戰性的基準數據集。

本文提出了一種多類迭代局部搜索（Multi-class Classification Iterated Local Search， MC-ILS）算法，該算法分別針對ITC競賽數據集和Lewis60數據集尋找可行的排課方案。該算法經過測試，并與當前文獻中成績較好的算法進行了比較。計算結果表明，所提算法具有優異的性能和更強的適應性，無論是在最小化軟約束違反值的ITC競賽數據集，還是在更難的硬約束條件下尋找可行解，均優于其他對比算法。

1 自動化排課問題模型

1.1 問題定義

排課問題的求解本質上是一個解決教室R={r1， r2，…， rm}、課時P={p1， p2，…， pn}、課程C={c1， c2，…， ct}等教育資源矛盾的多因素優化決策過程。

在模型中，定義X為候選解課表，每周d天，每天h節，一周總時段數n=d×h。xij為安排在ri教室pj時段的課程，事件G={g1，g2，…，gs}是綁定了教師、學生和第幾次課信息的課程集合，|G|=∑ti=1cli，cli為第i個課程每周需上的次數。conij為課程ci和cj的沖突情況，有沖突為1，無沖突為0。exclij為課程ci是否可安排到時段pj，可安排為1，不可安排為0。stui為課程ci的學生數，rmi為教室ri的座位數，rni為課程ci分配的房間數。dmi為課程ci要求的最小工作日，dni為X中課程ci的實際工作日。Cri為專業i的課程集合，Cr={Cr1，Cr2，…，Crs}為專業的集合，cpi， j為Cri里的課程是否被安排在pj時段，安排為1，未安排為0。

根據要解決的問題及參數定義，具體的硬約束和軟約束描述及相應的數學表達式如下。

1.2 硬約束及其數學表達

2 基本迭代局部搜索算法

局部搜索算法的基本思想是首先找到一個或一組初始解，然后按照一定的策略在鄰域中搜索新的可行解，并根據特定的接受準則更新當前解，最終找到最優解。局部搜索算法具有結構簡單，易理解易實現的優點，但由于其搜索性能過于依賴鄰域結構和初始解，容易陷入局部最優。

模擬退火算法作為一種經典的局部搜索算法，其靈感源自物理中固體退火原理，固體的結晶狀態通常是內能最小的狀態。將固體加溫至充分高，此時，固體內部粒子呈隨機排列狀態，內能增大;再讓其逐步降溫冷卻，此過程使得粒子趨于有序，每個溫度都能達到平衡態，最后常溫時達到內能最小的基態。根據Metropolis準則，粒子在溫度T下趨于平衡的概率為exp（-ΔE/（kT）），其中：E是溫度T處的內能，ΔE是變化量，k是玻爾茲曼常數。與之相對應，模擬退火算法的過程是首先找到一個初始解作為當前解，并設定一個初始溫度值T，然后按照一定的策略在鄰域中搜索新的候選解，計算候選解與當前解之間的差值ΔE，按照概率exp（-ΔE/（kT））接受候選解為新的當前解。在不斷迭代的過程中對溫度T逐步降溫，不斷減少差解的接受概率，最終找到近似解。

迭代局部搜索算法是對局部搜索算法的一種改進，通過對局部尋優策略的迭代調用來跳出局部最優。在每次迭代中使用前面局部搜索得到的最優解作為本次搜索的初始解，以此反復來獲取全局最優解。

3 多類迭代局部搜索求解排課問題

基本迭代局部搜索算法主要用于函數優化，將其應用于自動化排課問題，需要在算法框架、初始化方法、鄰域設計、模擬退火等方面進行改進。

3.1 算法主框架

在啟發式算法的設計中，待解決問題自身的特征往往決定了算法的具體設計細節，需要對每一個具體問題設計專門的解決辦法，很難用一個通用算法解決所有問題。本文提出一種多類迭代局部搜索（MC-ILS）算法來求解排課問題，通過對各種排課問題特征的分析抽取并用多類分類器進行分類，指導迭代局部搜索過程，實現自動化排課。具體步驟如下：

3.2 多類分類器

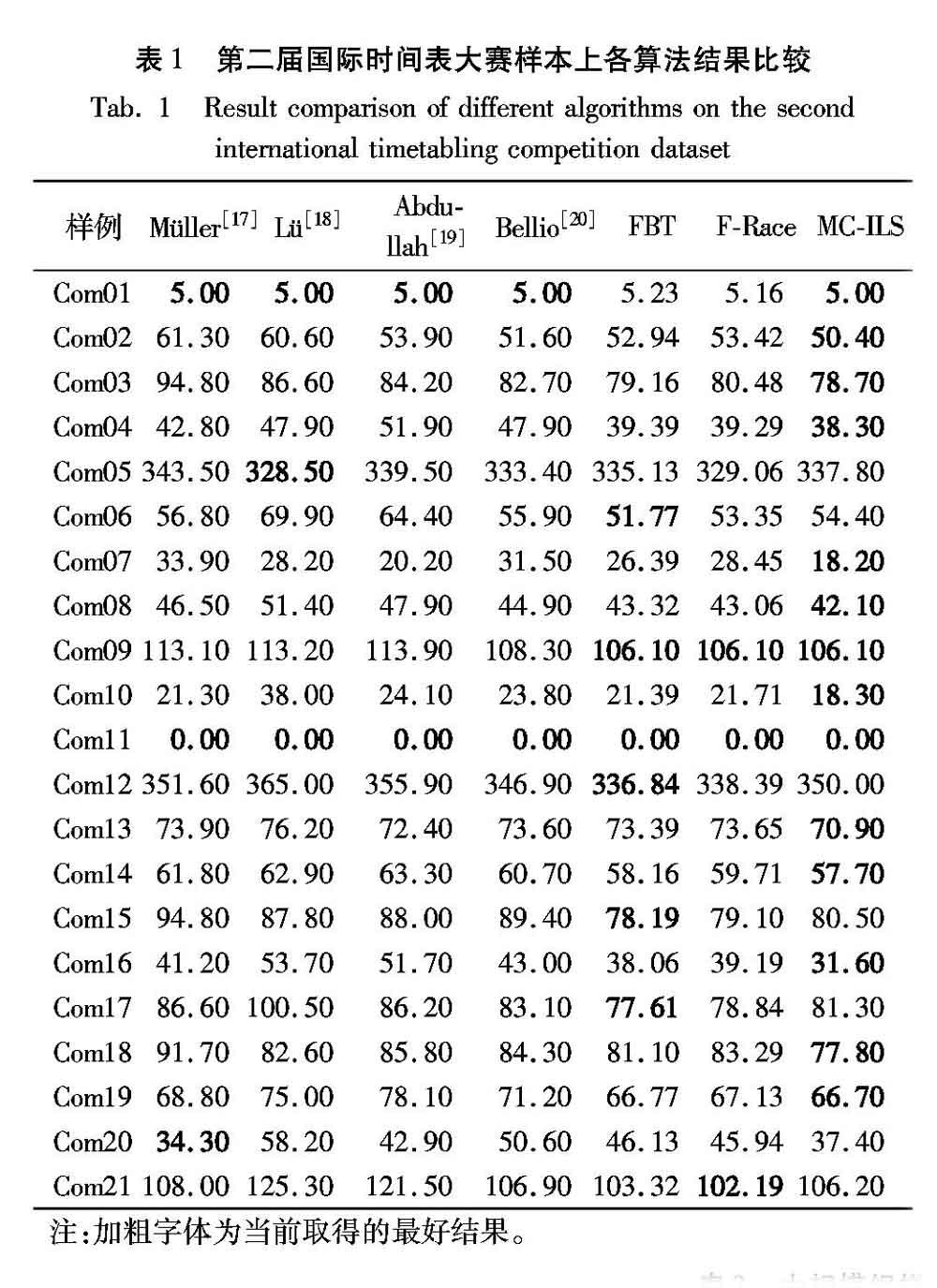
不同的排課問題具有不同的條件和約束，需要依據是否有軟沖突、房間數、時段數、課時約束等特征條件，對算法步驟中的實現進行參數調整和過程選擇。針對該問題，采用超啟發算法雖然可以提高排課算法的適應度，但也帶來算法和時間復雜度的提升。本文采用基于決策樹的多類分類器實現局部搜索算法的選擇和參數的設定，簡化算法結構和運行時間。決策樹構造如圖1所示。

決策樹第一層節點（問題類型）根據軟硬約束構造，判別僅存在硬約束還是軟硬約束均存在，第二層節點（問題難度）根據房間數和事件數等條件構造。為簡單起見，計算所有樣例事件數與房間數的比值，依據中值分為難易兩類，在實踐中此種劃分并不總是精確，因此需要再通過第三層節點（問題特征）對問題進行更精確的劃分。當決策樹構造完畢后，就采用決策樹算法對不同算例進行分類。