一種改進的基于加權屬性的SLOF離群點挖掘算法

趙向兵

（1.太原科技大學計算機科學與技術學院，山西太原 030024；2.山西大同大學數學與計算機科學學院，山西大同 037009）

一種改進的基于加權屬性的SLOF離群點挖掘算法

趙向兵1，2

（1.太原科技大學計算機科學與技術學院，山西太原 030024；2.山西大同大學數學與計算機科學學院，山西大同 037009）

SLOF算法采用了空間對象的空間屬性和空間關系確定空間鄰域，并結合非空間屬性的權值來計算對象在其鄰域內的離群度，但在計算屬性權值時，仍然由鄰域專家決定，存在人為因素。文中采用計算每個對象的每個非空間屬性的去一劃分信息熵增量，并通過這個值來反映各個屬性對對象離群的貢獻程度，給出一種改進的SLOF算法。實驗結果表明，算法具有計算效率高和對用戶依賴性小的優點。

高維數據；信息熵；息熵增量；屬性權值；偏離因子

離群點檢測是數據挖掘的重要分支之一，其目的是在大量的、復雜的數據集合中消除噪音數據或發現有意義的知識。Hawkins對離群點的定義抓住了概念的精髓：“一個離群點是一個觀察點，它偏離其它觀察點如此之大以至引起懷疑是由不同機制生成的”［1］。典型的應用領域包括在電子商務的犯罪行為探測、網絡入侵檢測分析。

離群點查找的算法很多，大體上可分為：基于分布的、基于深度的、基于距離的、基于密度的和基于聚類的［2］。近年，Shekhar，Lu和Zhang學者最先提出二分算法［3］，該算法將空間屬性與非空間屬性區分開，并用對象與其鄰域的非空間屬性的比值或差值，來表示對象與其鄰域的偏差，簡稱為SLZ算法。SLZ算法沒有能夠解決空間數據的異質性問題，因而，檢測的結果主要是全局離群點。Cbawla和Sun學者同時考慮了空間數據的異質性和自相關性，入波動參數β，且用β和對象與其鄰域的歐拉距離的乘積表示空間局部離群度SLOM［4］。但由于對稱分布狀況決定β，若其在波動幅度較小或空間鄰居較少的情況下，很難準確的表現波動情況，因而出現漏檢和誤檢現象。為此，薛安榮等人提出了一種SLOF算法［5］，該算法用計算鄰域距離的方法解決空間自相關性問題，用計算空間局部離群系數的方法來解決空間異質性問題，用對象的鄰域距離與鄰域中對象的平均鄰域距離之比表示對象的空間局部離群程度。但此算法在屬性權值的確定上，仍然由鄰域專家決定，存在人為因素。

本文針對SLOF算法中屬性權值確定方面存在的問題，給出了一種SLOF改進型算法，該算法采用計算每個對象的每個非空間屬性的去一劃分信息熵增量，來確定屬性權值，從而消除人為因素，并使算法的用戶依賴度進一步減少。

1 基本概念和定義

1.1 信息熵

信息熵是信息論中信息和隨機變量的不確定性的一種度量［6］。設X是一個隨機變量，其取值集合為S（X），p（x）表示X的概率函數，則X的信息熵定義為：

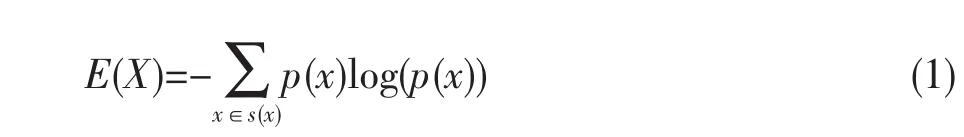
說明隨機變量的不確定性越大，信息熵就越大；信息熵值越小，不確定性越小。

1.2 去一劃分信息熵增量

設D是對象集合，D的一個子集是S，并且｜S｜＞1，設q是S中的一個對象。則S被對象Q劃分為S-｛q｝和｛q｝兩個部分，記為=｛C1，C2｝，得到。則E（S）-E（）為子集S去一劃分信息熵增量，記為Δ（q，s），S明確的情況下，在下文中簡記為Δ（q）。

可以看出Δ（q）表示S被劃分為C?的前后信息熵的變化。從統計角度看，離群點挖掘的關鍵是檢測出在全局中占百分比小的數據對象，因為在子集S中Δ（q）值大的對象正是占百分比小的對象，這些對象更有可能是離群對象。也就是說離群點是指數據集合中一旦離群點被刪除，整個數據集的“混亂”或“不確定性”就明顯減少的數據點。對于對象集合中的某個對象來說，這個對象的每一個非空間屬性對這個對象的離群貢獻度的大小，就是看一下這個對象每一個非空間屬性值在它所對應的非空間屬性值集合中的去一劃信息熵增量值的大小，即Δ（q）。所以我們用這個Δ（q）要表示非空間屬性的權值。

1.3 相關概念

空間鄰居：對象d的空間鄰居是指與對象d在指定條件c下，存在空間鄰接關系σc的對象。即?d∈D，?p∈D｛d｝，使得s（p）σcs（d）為真，則對象P是對象d的空間鄰居［5］。

空間鄰域：對象d的空間鄰域N（d）是指對象d的所有空間鄰居的集合，即

?d∈D，N（d）=｛p｜s（p）σcs（d）=ture，p∈D｛d｝｝

加權距離：在對象集D=｛d1，d2，…，dn｝，對象di，dj∈D，di和dj的M-維非空間屬性是f（di）和f（dj），則數據對象di，dj之間的M-維非空間屬性加權距離

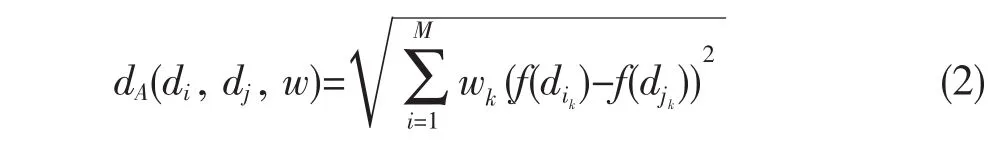
其中：wk是第k維的權值，且0≥wk≥1（這里是對wk做了歸一化處理），這個距離表示了兩個對象間的偏差。

平均距離：對象d的平均距離是指對象d與其空間鄰域中所有對象的加權距離的平均值，即

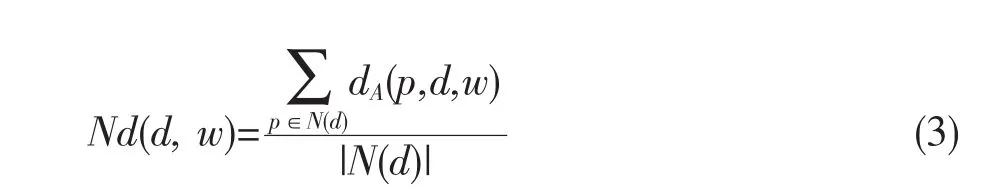
平均距離表示對象與其鄰域非空間屬性上的偏差，偏差大的離群度就越高。

對象領域密度

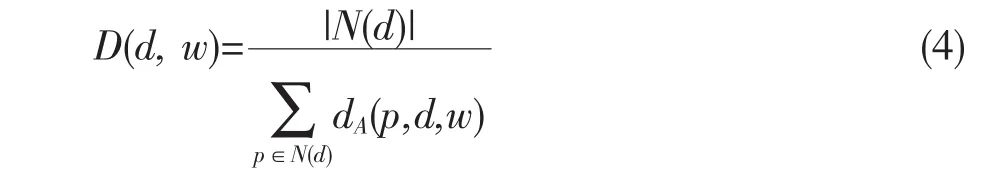
空間局部離群度：空間對象d所有鄰居的鄰域密度平均值與d的鄰域密度的比值得到d的空間鄰域偏離因子，即：

KSLOF（d）反映對象d的非空間屬性偏離它周邊鄰居的程度。

2 用去一劃分信息熵差量確定非空間屬性的權重

在計算對象間非空間屬性距離的時候，不同屬性對分析目標的貢獻程度不同，可用熵權作為非空間屬性重要程度的度量。倪巍偉等對屬性權值的確定提出了離群屬性子集的概念，用局部信息熵描述數據點及其鄰域近數據點在屬性上投影的分布情況計算離群屬性的參考值，組成離群屬性子空間，屬于此空間的屬性賦以大于1的λ值，不屬于此空間的屬性賦1。這樣同樣沒有對屬性的權值做具體的量化，難于區分λ的具體值，且計算時比較復雜，也比較抽象。而SLOF算法對屬性權值確定的方法主要是對非空間屬性做規則化處理。根據分析需要，給不同貢獻度的屬性分配不同的權值，貢獻度大的權值大，反之則小，權值一般由鄰域專家決定。所以這種方法，沒有對每個屬性的貢獻度做具體量化，且很難解釋，計算的數值有人為化因素，很難對分析數據做推廣。而去一劃分信息熵增量很好的解決了以上問題，方法如下：

設對象集合D=｛d1，d2，…，dn｝，由n個對象組成，對象d∈D的空間屬性函數s（d），非空間屬性函數是f（d），f（d）的維度是m維，m維非空間屬性f（d）表示為（f（d1），f（d2），…，f（dm））

按照定性和定量結合的原則得對象非空間屬性矩陣：

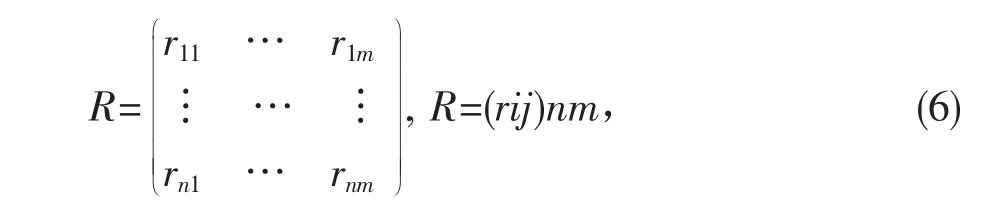
rij表示第i個對象在j-屬性上的值。且可以得出：f（dj）=rij（i=1，…，n，j=j）。

設p是m個對象中的第j個對象，所以p對象可以包含矩中m個值且每個值分別對應對象的m個屬性值。接著我們可以分別計算這m個屬性值在它所對應的屬性取值集合中計算去一劃分信息熵增量，分別記為Δ（p1），…，Δ（pm）。

對于p，在m維非空間屬性中，第j維屬性的權值記為wj，且wj=Δ（pj），（j∈m）。

根據去一劃信息熵增量的意義可知，對于對象p來說，在每個屬性上Δ（q）值越大，對象p的離群度就越大，它所對應的屬性的離群度就越大，它的屬性權值就越大。進而根據屬性權值確定不同屬性對分析目標的貢獻程度。

3 改進的SLOF離群點檢測算法

根據上述分析，采用計算每個對象的每個非空間屬性的去一劃分信息熵增量，來確定屬性權值，從而有效地消除人為因素。其算法描述如下：

輸入：對象集D=｛d1，d2，…，dn｝（對象di的空間屬性函數s（di），非空間屬性函數是f（di），σc表示在指定條件c下的空間鄰接關系，m維非空間屬性f（di）表示為（f（dj1），f（dj2），…，f（djm）））。

輸出：離群度最大的前q個對象

Step1：從集合D中取一對象d，從D中尋找與d存在空間關系σc的所有鄰居，并確定對象d的鄰域N（d）；

Step2：利用（1）式和（6）式分別計算對象d在非空間屬性（f（d1），f（d2），…，f（dm））中各個屬性的去一劃分信息增量值，分別記為Δ（p1），…，Δ（pm）。從而確定對象d的非空間屬性的權值分別為wj，且wj=Δ（pj），（j到m）；

Step3：把wj代入（2）式計算加權距離，并利用（3）式計算對象d與空間鄰域中所有對象的加權距離的平均值；

Step4：利用（4）式和（5）式計算對象d的空間局部鄰域偏離因子KSNOF；

Step5：計算集合D中其它每個對象的空間鄰域偏離因子KSNOF；

Step6：把所對象的空間鄰域偏離因子KSNOF按降序排列；

Step7：輸出前q個對象，前q個對象就是空間離群點。

分析上述算法，該算法的復雜度為：O（n（klogsn+km+log2n））（k為對象的鄰居數），而LOF等算法確定鄰域卻采用的是全部屬性，其復雜度為O（kn2），所以采用此算法離群點檢測效率比較高。

4 實驗

試驗環境：CoreT7500 2.2G CPU，2G內存，操作系統為Windows 2000，數據庫為SQL，并采用VC++編寫了上述算法。采用某省旅游景點情況統計數據，以200個旅游景點為研究對象，數據中既有空間屬性又有非空間屬性。對于各個景點，與它相鄰的景點可以組成其鄰域。選擇5個非空間屬性：tourists，greenrate，complaints，facilitation，satisfaction。通過20個景點評價對象計算得這五個非空間屬性權值p=｛0.18，0.20，0.15，0.19，0.33｝。實驗結果表明，這種算法檢測出的5個離群點確實是鄰域離群點，見表1。

表1 SLOF算法挖掘的5個離群點

為了進一步考察算法的性能，用LCK算法和SLZ算法與該算法進行比較，如圖1所示可知，該算法傾向于挖掘鄰域離群點，而SLZ算法和LCK算法偏向挖掘全局離群點，采用改進型SLOF算法的檢測精度較高，并且準確給出了其它離群數據對象的離群順序。也證明了改進型SLOF算法結果的得出是充分的考慮了空間數據的相關性和異質性的結果，而SLZ算法和LCK算法都造成了局部離群點的漏選。從時間執行上來看，由于空間屬性確定鄰域最費時間，這三種算法采用相同的數據和算法，因而確定鄰域的執行時間一樣，比較總執行時間應在同一數量級上，執行時間分別為SLOF：3.5s，SLZ：3.8s，LCK：4.1s。如果再把數據對象和維數做人工擴充，隨著對象和非空間屬性維數的增加，SLZ算法和LCK算法執行效率會下降，執行時間也會增加，但改進型SLOF算法卻有著很好的伸縮性，執行時間增加幅度小于SLZ算法和LCK算法，因而它有著更好的性能。

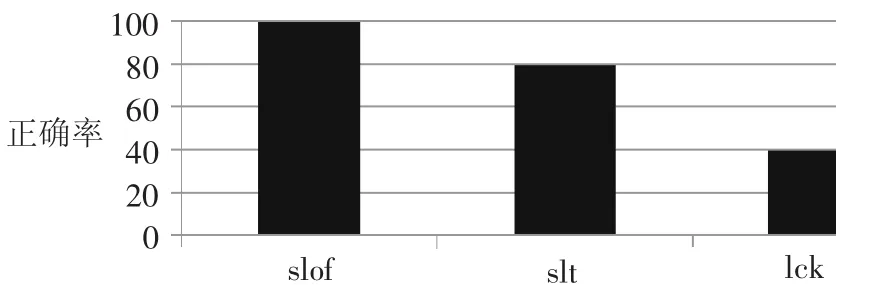
圖1 檢測結果比較

5 結語

該算法充分考慮了空間數據的特點，根據空間關系確定空間鄰域，減少了用戶指定參數，特別是在非空間屬性的處理上，通過計算每個屬性去一劃分信息熵增量來確定屬性權值。進而確定非空間屬性的離群程度。此算法是對SLOF算法的改進，且易于解釋，去除人為因素的干擾。實驗表明，該算法在減少用戶依賴度、提高檢測精度上具有明顯的優勢。

［1］Hawkms D.Identification of Outliers［M］.London：Chapman and Hall，1980.

［2］Han Jiawei，Kamber Micheline.Datamining：concepts and techniques［M］.San Francisco：Morgan Kaufmann Publishers，2001.

［3］Gulukota K，Sidney J，Sette A，et a1.Two complementary methods for predicting peptides binding major histocompatibility complex molecules［J］.Journal of Molecular Biology，1997，26：1258-1267.

［4］Brusic V，George R，Margo H，et a1.Prediction of MHC class II-binding peptides using an evolutionary algorithm and artificial neural network［J］.Bioinformatics，1998，14：121-130.

［5］薛安榮，鞠時光，何偉華，等.局部離群點挖掘算法研究［J］.計算機學報.2007，30（8）：1457-1458.

［6］Claude E S.A mathematical theory of communication［J］.Bell System Techical Journal，1948（27）：623-656.

〔編輯 高海〕

SLOF based on Weighted Attribute of the Improved Algorithm for Outliermining

ZHAO Xiang-bing1，2
（1.School of Computer Science and Technology，Taiyuan University of Science＆Technology，Taiyuan Shanxi，030024； 2.School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

SLOF algorithm uses spatial properties and spatial relationships of spatial objects to determine spatial neighborhood and combined with the weight of non-spatial attributes to calculate the object＇s outlier in its neighborhood.However，the attribute weights are still determined by the neighborhood experts in the calculation，there are human factors.For each object，calculating leave-one division information entropy increment of each non-spatial attribute is introduced in this article when determining the right value of non-spatial attribute.This value can reflect the contribution of stray objects by the various attributes and furthermore an improved SLOF algorithm is given.Experimental results show that the algorithm has high computational efficiency and the advantage of less dependence on the user.

high dimensional data；entropy；entropy increment；attribute weights；deviation factor

O211.7

A

1674-0874（2011）03-0011-03

2011-02-06

趙向兵（1978-），男，山西大同人，在讀碩士，助教，研究方向：數據挖掘。