雙層金屬平板模擬機匣抗沖擊性研究

楊 樂，關玉璞，張 濤，陳 偉

（南京航空航天大學能源與動力學院，南京 210016）

0 引言

航空發動機轉子以很高的轉速運轉，當轉子葉片在工作中意外失效時，斷裂的葉片碎塊會以巨大的能量被甩出，嚴重威脅飛行器的安全。中國民航航空發動機適航規定和通用規范均要求壓氣機和渦輪轉子機匣必須對轉子葉片失效引起的破壞具有包容性。為了提高效率，現代航空發動機高壓壓氣機機匣和低壓渦輪機匣通常設計為雙層金屬結構。因此，研究雙層機匣的包容性具有重要的工程應用意義。

航空發動機機匣包容能力的驗證通常花費極其昂貴，在機匣設計初期，一般通過研究不同的材料和結構形式的抗沖擊性能，預估機匣的包容能力。公開發表的雙層機匣抗沖擊性能研究的文獻極少，多數雙層結構抗沖擊性研究基于彈體穿甲。彈體穿甲與機匣結構不同的是采用靶板較厚，彈體的形狀多為圓柱形，且撞擊速度較高，因此彈體穿甲的研究結論只能作為參考。Ben-Dor[1]通過簡化的錐形彈體沖擊雙層板模型，分析了層間距對雙層延性金屬材料平板的影響，結果表明，隨著層間距的增加，雙層金屬板的彈道極限速度可能增加，也可能降低。Dey等[2]結合試驗和數值仿真研究了3種不同鋼板抗侵徹性能，在鈍頭沖擊下，隨著材料強度的提高，鋼板的彈道極限速度呈下降趨勢，在錐形或者頭部有尖拱的彈體沖擊下，鋼板的彈道極限速度與之相反。Huang[3]數值模擬了鈍頭彈體沖擊雙層厚度為6 mm、層間距為3 mm鋼板的彈道沖擊性能，模擬結果表明，雙層鋼板在鈍頭彈體沖擊下的失效模式為拉伸撕裂，且其抗沖擊性能比同等厚度的單層板彈道極限速度提高25%。Teng等[4]的研究結果與Huang[3]的一致。Dey等[5]通過試驗與分析厚度為6 mm、層間距為24 mm的Weldox 700E鋼板認為，在純頭彈體沖擊時，雙層結構的彈道極限速度可以比單層結構的提高40%；在尖拱彈體沖擊時，雙層結構彈道極限速度與單層結構的相當。Teng[6]在前人的研究基礎上，利用數值模擬分析了雙層無間隙厚度為6 mm，不同材料鋼板在鈍頭和尖頭彈體沖擊下的抗沖擊性能。研究結果表明，內層采用高延性低強度材料，外層采用低延性高強度材料結構的抗沖擊性最佳。Abdel-Wahed等[7]利用小口徑彈體發射器研究了尖頭彈體沖擊單層厚度為3 mm和等厚的多層鋼板。結果表明，單層板的抗沖擊性能優于相互接觸和有間隙的多層板。影響雙層結構抗沖擊性能的因素很多，如彈體的形狀、撞擊速度、靶體的間距和厚度分配等。

本文采用結構動力學分析軟件LS-Dyna，對葉片正撞擊時，雙層金屬平板模擬機匣的損傷模式進行了數值模擬，并討論了層間距和厚度分配對雙層金屬平板抗沖擊性的影響。

1 分析模型

1.1 幾何模型

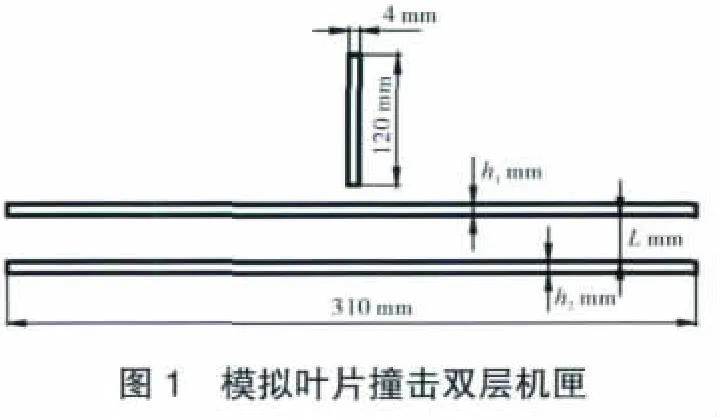
模擬葉片和雙層平板的材料均為1種馬氏體型熱強不銹鋼1Cr11Ni2W2MoV。其室溫拉伸強度、持久強度極限及蠕變極限均較高，材料力學性能參數見表1。模擬葉片的尺寸為120 mm×50 mm×4 mm，平板長310 mm，寬 250 mm，雙層平板總厚度為3 mm，內層板厚為 h1，外層板厚為h2，層間距為L，模擬葉片撞擊雙層機匣如圖1所示。

?

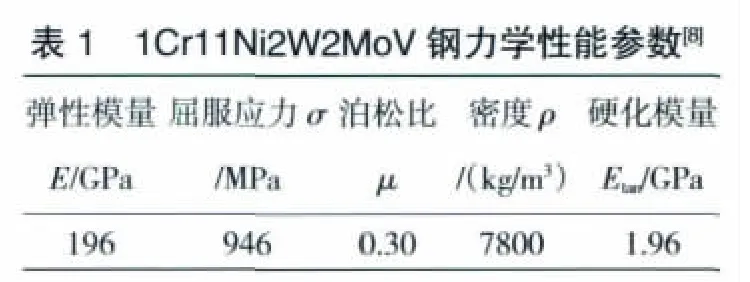
1.2 材料模型

在數值仿真時，對葉片和靶板均采用隨動塑性材料模型，該模型是1種考慮應變率效應的雙線性硬化塑性模型[9]。硬化參數b可在0（僅隨動硬化）到1（僅各向同性硬化）之間選擇，用來調整材料中各向同性硬化與隨動硬化的影響，通過定義失效應變刪除失效單元。屈服應力通過引入考慮了應變率的Cowper-Symonds模型來表示。

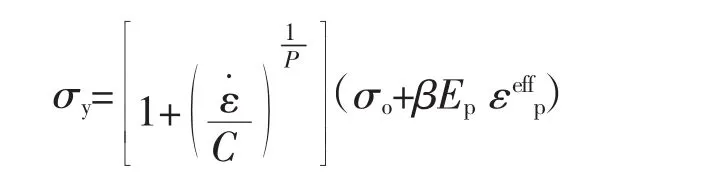
式中：σ0為初始屈服應力為有效塑性應變；ε˙為應變率；C、P為Cowper-Symonds應變率參數；Ep為硬化模量

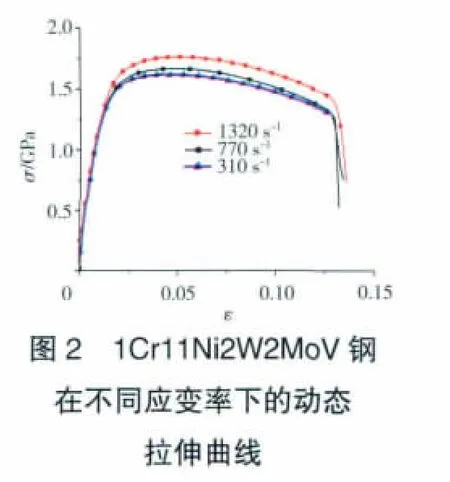
材料的靜態力學性能參數通過查找材料手冊確定；應變率參數C、P和失效應變需要動態試驗進行擬合測定。為了準確得到雙層平板材料模型中動態性能參數，采用范志強關于1Cr11Ni2W2MoV不銹鋼的動態試驗數據[10]，其在不同應變率下動態拉伸曲線如圖2所示，對該曲線進行擬合，得到應變率參數 C=40000，P=5，失效應變εfailure=0.1。

1.3 有限元模型

葉片與雙層板均選用實體Solid 164單元和單點積分算法。葉片沿長度方向分40份，寬度方向分25份，厚度方向分4份，共4000個單元。平板的網格密度對撞擊計算結果較為敏感，Raguraman等[11]的研究表明，網格大小接近2 mm能夠很好地模擬薄板撞擊的剩余速度，綜合考慮計算精度和計算時間，將平板沿長度方向分為150份，寬度方向分125份，厚度方向分4等份，每層平板分為75000個單元，網格劃分結果如圖3所示。數值仿真時對平板寬度方向2邊施加全約束，其余邊自由。

采用面對面侵蝕接觸方式（Erode Surface-to-Surf）定義葉片與雙層板以及雙層板之間的接觸，其中平板為目標體，葉片為接觸體。在計算模型中，適當調整黏性阻尼系數，控制接觸力引入的噪聲；通過調整沙漏算法，抑制沙漏模式。

2 雙層平板的沖擊響應

葉片撞擊速度為90 m/s，雙層厚度各為1.5 mm，層間距為10 mm平板沖擊整體變形的塑性應變響應如圖4所示。從圖中可見，葉片在0.08 ms開始撞擊內層平板，在葉片前、后緣位置，內層板塑性變形最大，損傷在撞擊瞬間貫穿至平板的背面。葉片穿透內層板到撞擊外層板約歷時0.08 ms，在0.24 ms時，內層板沿撞擊方向的變形達到最大，葉片開始撞擊外層平板，外層板的損傷模式與內層板的相同，在葉片接觸的瞬間的葉片前、后緣位置，外層平板的塑性變形最大。從LS-Dyna后處理器LS-PREPOST觀察到葉片穿透外層板約歷時0.16 ms。

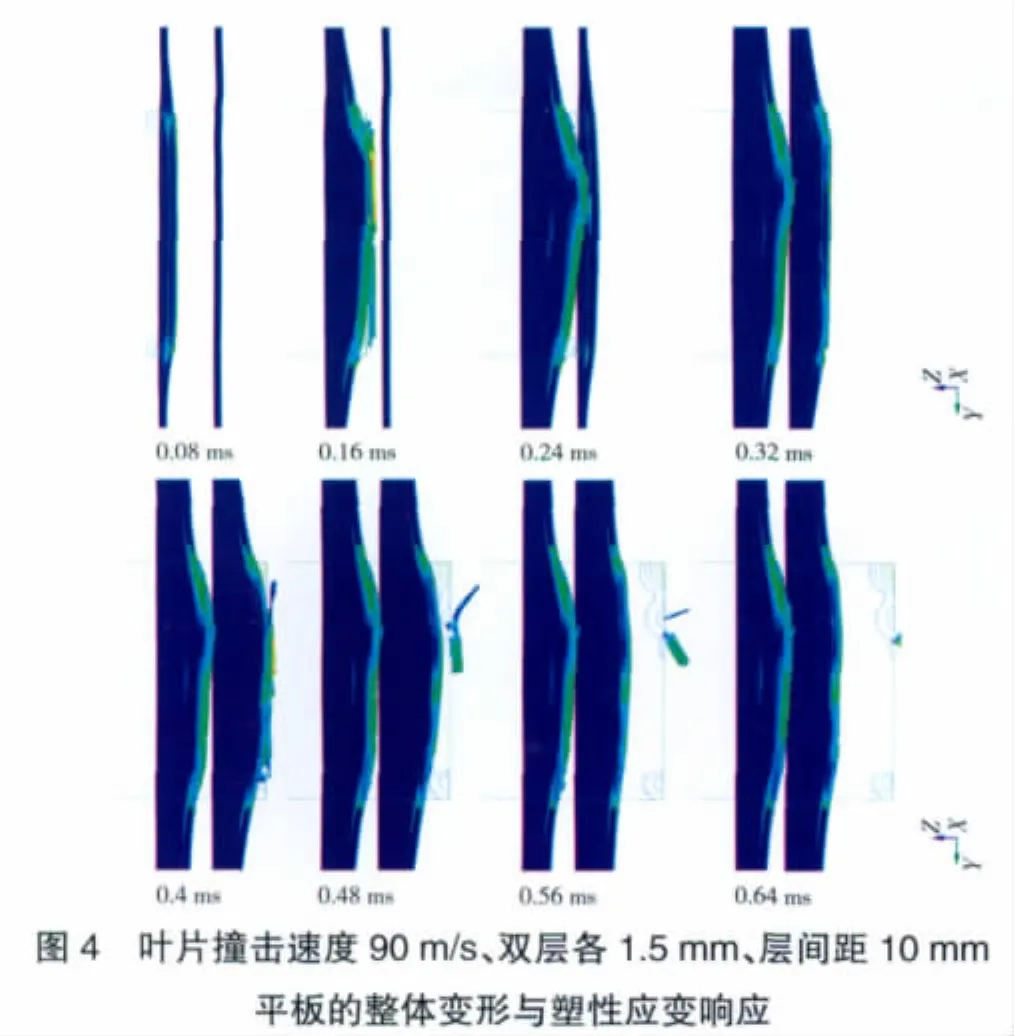
在葉片正撞擊時，內、外層板的損傷是由于撞擊區域局部剪切和整體塑性撓曲變形引起的，而局部的剪切是導致平板最終破裂的主要原因。平板在撞擊體的作用下，有明顯的彎曲變形和背面隆起。平板破裂后，隆起部分伴隨有明顯的花瓣狀變形，同時產生徑向裂紋，并卸載周向應力，逐步沿著葉片的棱角向外擴展，形成背面的花瓣運動的動量。在葉片穿透過程中，局部的剪切失效和整體的彎曲變形是平板消耗撞擊能量的主要途徑。在葉片撞擊過程中，雙層板破裂形式基本相同，因此認為破裂過程中消耗的塑性功相等，決定內、外層板吸收能量大小的主要因素應該為整體塑性變形消耗的塑性功。

2.1 層間距對雙層板抗沖擊性的影響

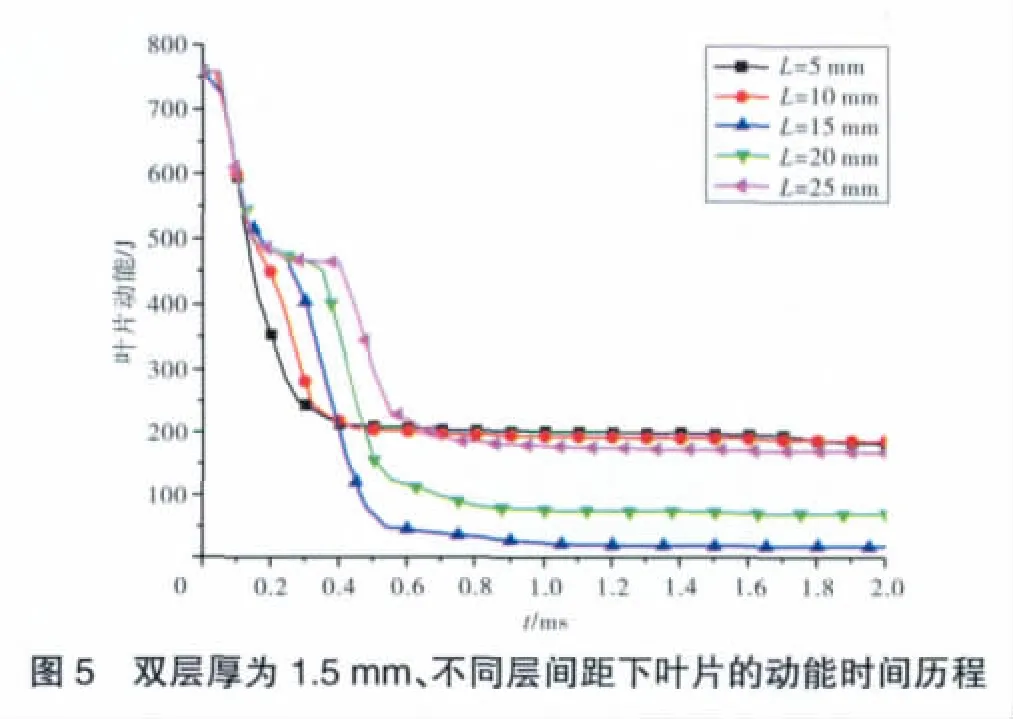
采用 h1＝1.5 mm、h2＝1.5 mm，層間距 L 分別為 5、10、15、20和25 mm的雙層平板，研究層間距對雙層平板抗沖擊性的影響。葉片以90 m/s的速度撞擊不同層間距等厚雙層板的動能時間歷程如圖5所示。從圖中可見，葉片穿透內層板后損失的動能相同，初始撞擊外層板的時間隨著層間距的增加而后延，葉片穿透外層板損失的動能差異較大；L＝15 mm時，葉片穿透外層板時動能損失最多，其次是L＝20 mm時的，再次是 L＝25 mm 時的，L＝5、10 mm 時，葉片損失的動能最少。雖然從數據上來看，應該存在1個在L＝15 mm附近的最優間距，但考慮到L＝5、10和25 mm時的基本相同，整體來看并無明顯規律，還應做進一步深入研究與試驗驗證。

L＝10、15和20 mm，內層板和外層板與單層厚為1.5 mm板撞擊速度為90 m/s的吸收能量情況如圖6所示。從圖中可見，在葉片正撞擊時，雙層板的內層板吸收能量與單層厚度為1.5 mm吸收的能量基本相同，受層間距影響最為明顯的是撞擊外層板消耗的能量。

因內層板吸收能量基本相同，所以葉片撞擊外層板的初始能量是相同的。由于層間距不同，從葉片穿入內層板開始至葉片撞擊外層板的時間間隔不同，故葉片與內層板之間作用時間亦不同，導致葉片撞擊外層板時撞擊角度發生變化，而這對撞擊過程影響十分明顯，造成了外層吸收能量水平有明顯差異。在不同層間距下，葉片穿透外層板過程中最大傾斜角度見表2。從表中可見，L＝15 mm、葉片穿透外層板時傾斜的角度最大為4.15°，其次是L＝20 mm時的，其余3組穿透角度變化不大。

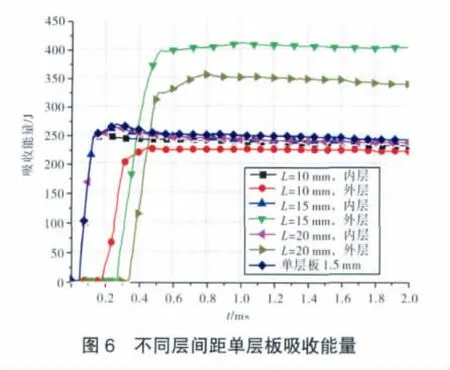
表2 不同層間距葉片穿透外層板時的角度

2.2 厚度分配對雙層板抗沖擊性的影響

雙層金屬平板總厚度為3 mm，定義厚度分配比η=h1h2。在撞擊速度為90 m/s、不同厚度分配時葉片的動能時間歷程如圖7所示，葉片動能損失量見表3。從表3中可見，當厚度分配η=1時，葉片損失的動能最少；當η=0.2時，葉片損失的動能最多；當η＜1時，葉片損失的動能隨著η的減小而增加；當η＞1時，葉片損失的動能隨著η的增大而不斷波動變化，但總體趨勢是逐漸增加的。

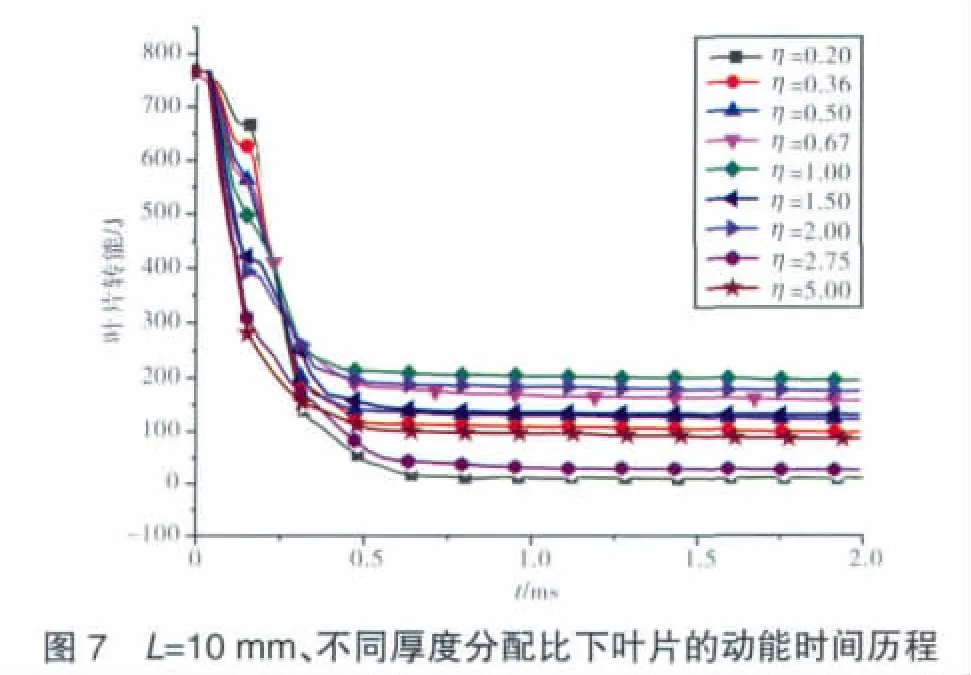
在葉片撞擊過程中，初始的葉片撞擊能量只有小部分轉化為葉片的內能，根據能量守恒定律，葉片損失的動能少就意味著雙層板吸收的能量少，反之則認為雙層板吸收的能量多，而雙層板吸收能量的多少決定其抗沖擊性的好壞。

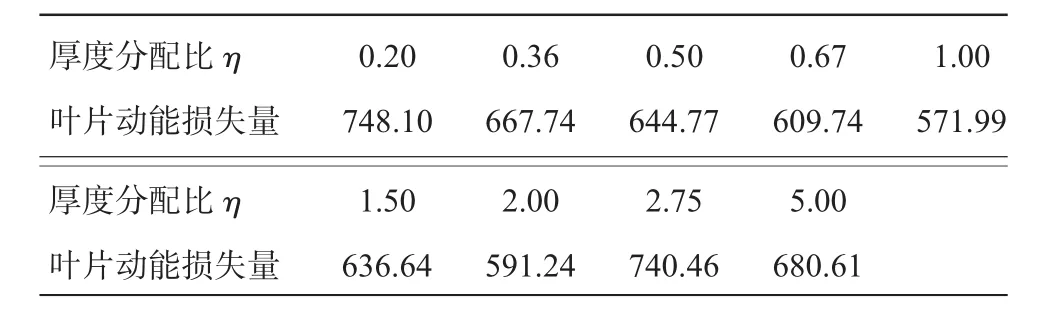
表3 不同厚度分配比時葉片動能損失量

可以總結為，L＝10 mm的雙層板，以厚度分配η=1為轉折點。當η＜1時，隨著η的減小雙層板的抗沖擊性能增強；當η＞1時，隨著η的增大，雙層板的抗沖擊性能總體上呈增強趨勢。

3 結論

（1）在葉片正撞擊時，內、外層板的損傷是由于撞擊區域局部剪切和整體塑性撓曲變形引起的。剪切力導致平板最終破裂，平板破裂后，裂紋沿著葉片的棱角向外擴展。

（2）對于厚度相同、層間距不同的雙層平板模擬機匣，隨著層間距的變化，雙層平板的抗沖擊性變化沒有一定的規律，這主要與外層板吸收能量的多少有關，其原因是葉片穿透內層撞擊外層板時，撞擊角度發生了傾斜。

（3）對于總厚度為3 mm、不同厚度分配比的雙層平板模擬機匣，當厚度分配比η＜1時，雙層板的抗沖擊性能隨著η的減小而增強；當η＞1時，雙層板的抗沖擊性能總體上隨著η的增大呈增強趨勢。

本文僅通過數值分析方法進行研究，未進行試驗對比驗證；且僅對總厚度為3 mm的雙層平板進行了研究，未考慮總厚度變化對雙層金屬平板抗沖擊性能的影響，有待進一步開展研究。

[1]Ben-Dor G,Dubinsky A,Elperin T.Effect of air gap and order of plates on ballistic resistance of two layered armor[J].Theoretical and Applied Fracture Mechanics,1999,31（3）：233-241.

[2]Dey S,B?rvik T,Hopperstad O S,et al.The effect of target strength on the perforation of steel plates using three different projectile nose shapes[J].International Journal of Impact Engineering,2004,30（8/9）:1005-1038.

[3]Huang Min.Ballistic resistance of multi-layered steel shields[D].Beijing：Material Science and Engineering,Tsinghua University,2005.

[4]Teng X,Dey S,B?rvik T,et al.Protection performance of double-layered metal sh ields against projectile impact[J].Journal of Mechanics of Material and Structures,2007,2（7）:1309-1329.

[5]Dey S,B?rvik T,Teng X,et al.On the ballistic resistance of double-layered steel plates:an experimental and numerical invertigation[J].International Journal of Solids and Structures,2007,44（20）:6701-6723.

[6]Teng X,Wierzbicki T,Huang M.Ballistic resistance of double-layered armor plates[J].International Journal ofImpact Engineering,2008,35（8）:870-884.

[7]Abdel-Wahed MA,Salem A M,Zidan A S,et al.Penetration of a small caliber projectile into single and multi-layered targets[C]//14th International Conference on Experimental Mechanics,Poitiers,France,2010.

[8]顏鳴皋.中國航空材料手冊:第1卷：結構鋼、不銹鋼[M].北京：中國標準出版社,1988:658-675.

[9]Hallquist J O.LS-Dyna theory manual[M].Livermore Software TechnologyCorporation,2005.

[10]范志強.航空發動機機匣包容性理論和試驗研究[D].南京：南京航空航天大學，2006.

[11]Raguraman M,Deb A.Accurate prediction of projectile residual velocity for impact on single and multi-layered steel and aluminum plates[C]//9th International LS-DYNA Users Conference,Hyatt Regency Dearborn Dearborn,Michigan USA,2006.