基于統計學檢驗指標的燃氣輪機部件特性方程擬合次數的選擇

趙雄飛，劉永葆，賀 星，劉建華

（海軍工程大學 船舶與動力學院，武漢 430033）

0 引言

在燃氣輪機氣路故障診斷過程中，針對所給出的燃氣輪機各部件特性曲線以及實際工作曲線，建立其部件特性方程，確定研究對象的精確數學模型，是實施正確診斷的必要前提。在一般情況下，采用曲線擬合的方法來建立部件特性方程。周密[1]在研究燃氣輪機氣路故障診斷中，采用最小二乘法對壓氣機與渦輪部件特性曲線進行擬合，取得了較好的擬合結果；Taik-Min Lee等[2]將精確的雙弧線擬合算法應用到非球面加工，擬合結果與球面實際情況吻合，為進一步分析奠定了基礎；賀星[3]針對燃氣輪機性能退化，在建模過程中采用了改進的麥夸爾特算法擬合部件特性曲線；袁萃等[4]在飛行器飛行仿真研究中，應用曲線擬合方法替代插值方法，減少了輸入參數數量，從而提高了仿真精度；方前[5]對風扇特性曲線進行擬合，考慮了邊界約束條件，提高了擬合精度；Verboven.P等[6]對多幅值相應曲線進行擬合，并將擬合結果用于模型的參數估計中，取得了較好的效果；曾嶸[7]將SVM算法中的回歸機應用于曲線擬合過程中，從而對機械故障進行診斷，但在實際擬合過程中，如何選擇合適的擬合函數與擬合次數，對其精確度有著至關重要的影響；劉喜超等[8]采用偏最小二乘法對壓氣機特性曲線進行了擬合，并用相對誤差和相關系數平方指標評價了擬合結果；Bo-Suk Yang[9]采用均方差、標準差線性關系度來評定擬合精度，均取得了較好的效果。趙世榮[10]提出了以訓練樣本、測試樣本誤差平方和的平方根作為建模的評價標準來評定所建模型的準確性。

本文以5種擬合檢驗指標，結合所選算法優選出最佳的特性方程擬合次數，使得到的擬合方程在最大程度上反映實際曲線運行規律，從而降低了建模誤差。

1 統計學檢驗指標的引入

本文引入5個統計學擬合檢驗指標，以檢驗特性方程擬合次數是否恰當，并計算得出最佳的擬合次數。

1.1 相關系數平方指標R2

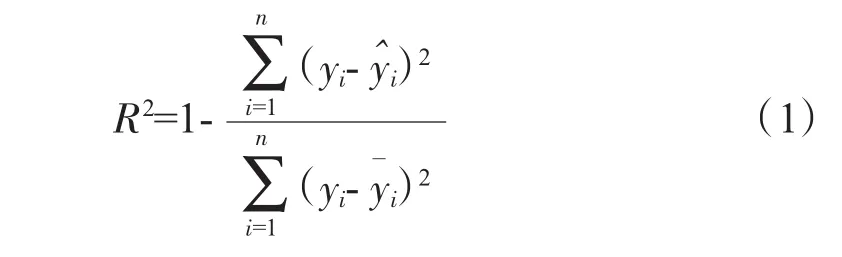
式中：yi為測量值為擬合值為樣本均值。

相關系數平方越接近1，擬合效果越好。

1.2 均方差指標RMSE

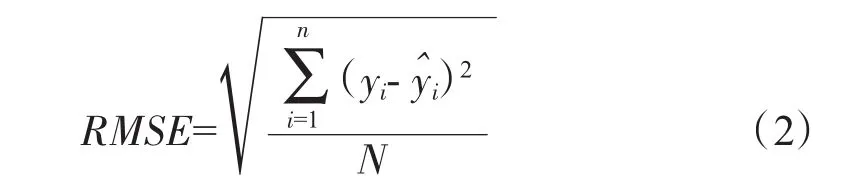
式中：N為實際測量樣本總數。

均方差越接近0，擬合效果越好。

1.3 相對誤差平方和SRES

相對誤差平方和越小，擬合效果越好。

1.4 檢驗指標Q1

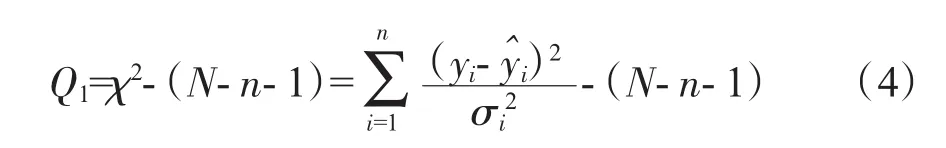
在式（4）中，假設yi服從正態分布，卡方系數χ2以自由度（N-n-1）為期望值。當 χ2-（N-n-1）越小，則擬合精度越高；在（N-n-1）附近時，擬合是合理的。反之，當＞＞（N-n-1），則可能是由選擇的擬合函數形式不合適、方差估計太小、樣本誤差等原因造成。其中n+1是多項式系數的數目。由于本文數據是通過部件特性曲線離散化后得到的結果，所以忽略后2種因素，檢驗指標Q1主要檢驗擬合函數是否符合樣本本身的內在規律。

1.5 檢驗指標Q2

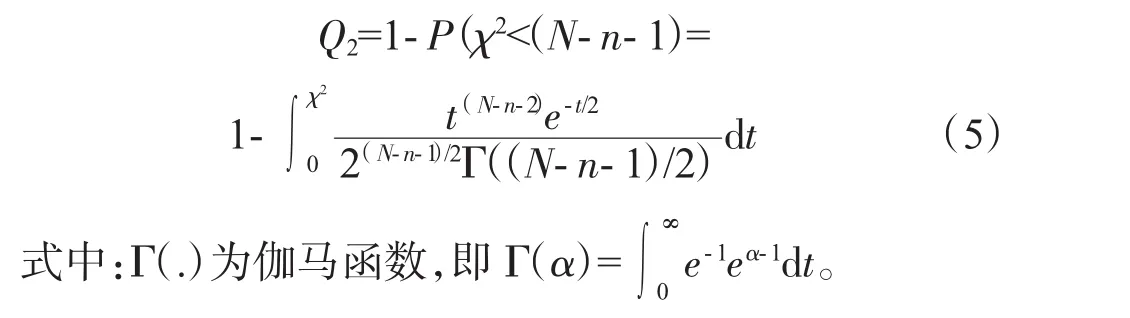
該檢驗指標Q2與0.5接近，則表示多項式擬合次數適當。

2 擬合模型的選擇

對于一般的特性曲線，通常采用多項式模型對數據進行描述，對于擬合目標形如 y（x）=f（a,x）=a1xn+a2xn-1+L+anx+an+1的n階多項式模型，通常要求取參數 a1、a2、L、an、an+1使下面的相對誤差 ψ2量最小。

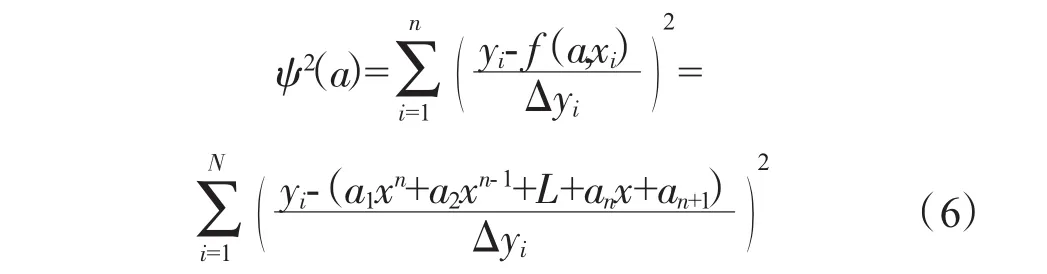
在Δyi=Δy不變的假設下得到式（6）的最小解為

通過對特性曲線進行多項式擬合得到特性方程。其實質是多元回歸問題，一般采用結合法[8]或2步法[11]，本文采用2步法對部件特性曲線進行擬合。

3 算例分析

3.1 擬合次數的選擇

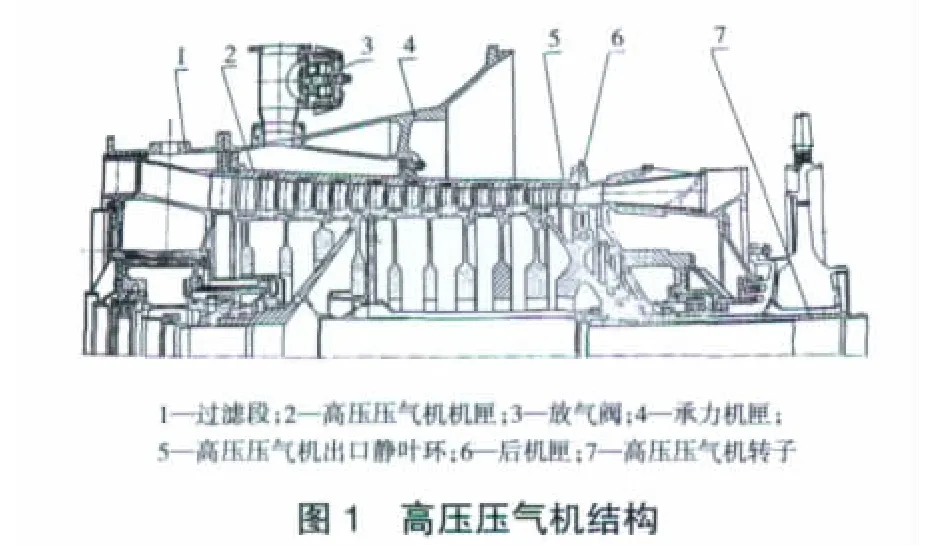
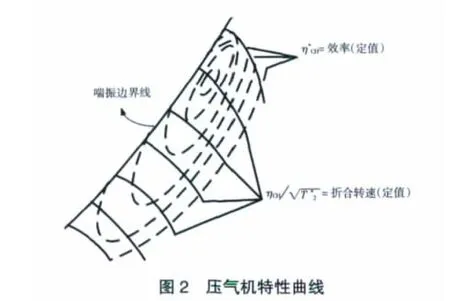
以某型3軸燃氣輪機的高壓壓氣機為例，其結構如圖1所示[12]，壓氣機通用特性曲線如圖2所示。從圖2中可見，高壓壓氣機折合流量與高壓壓氣機壓比和折合轉速存在一定的函數關系。將壓氣機壓比與折合轉速作為自變量，而將折合流量作為因變量，4個參數之間存在如下關系

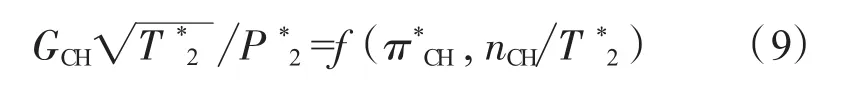
用多項式進行曲線擬合，當最高次數n≥7時，經過大量計算及理論分析均表明其方程的系數矩陣是嚴重病態的。所以考慮最高次數n≤6時對高壓壓氣機的1.0工況等轉速線上的“折合流量-壓比”關系曲線進行研究，并按照擬合檢驗指標尋找并確定“折合流量-壓比”之間的最佳函數關系，其結果見表1。

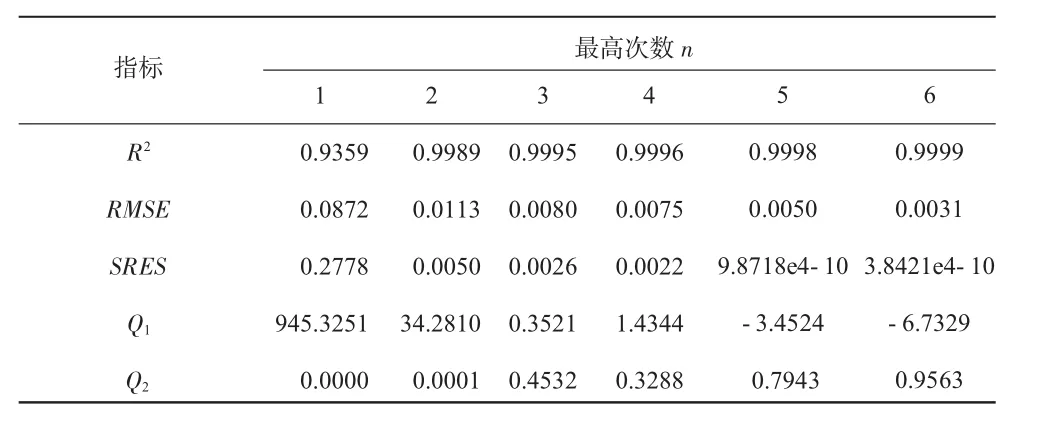
表1 不同最高擬合次數檢驗指標值

從表1中可見，隨著擬合次數n的增加，R2、RMSE、SRES呈越來越好的趨勢。由此表明，在特性曲線多項式擬合中，隨著擬合次數的增加，精度提高。但是，從Q1、Q2可知，在n≥4時的擬合過程中出現過擬合，擬合曲線納入了噪聲，所以，在保證擬合精度的前提下有避免納入噪聲的原則，這里選擇n=3作為該曲線的最佳擬合次數。

3.2 擬合誤差分析

選擇n=3作為部件特性方程的擬合次數，可以得到該測量值與擬合值的相對誤差，如圖3所示。

從圖3中可見，當選擇n=3時，對應的各工況下的最大誤差為0.2%，其結果滿足擬合精度。根據上述分析，繪出在擬合曲線中原數據點與擬合點的對比曲線，并給出其殘差分布情況，其結果如圖4所示。

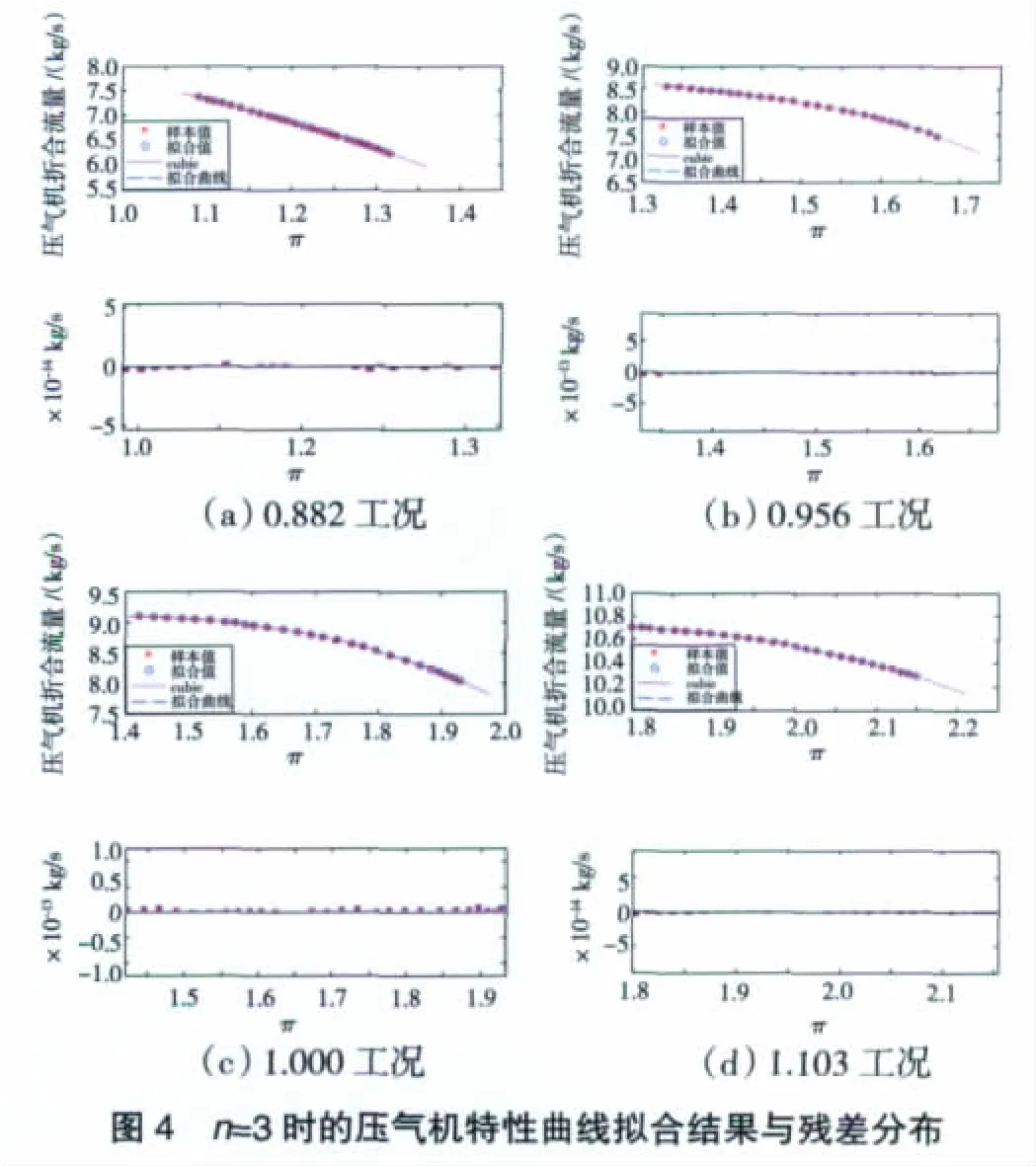
從圖4中可見，通過正確地選擇擬合次數，其所得到的擬合曲線殘差為±5×10-13，擬合效果較好。

3.3 擬合結果

上述分析可知壓氣機折合流量是關于壓比與折合轉速的函數，所以首先通過1次擬合分別得到各工

況下關于“折合流量-壓比”之間的函數關系

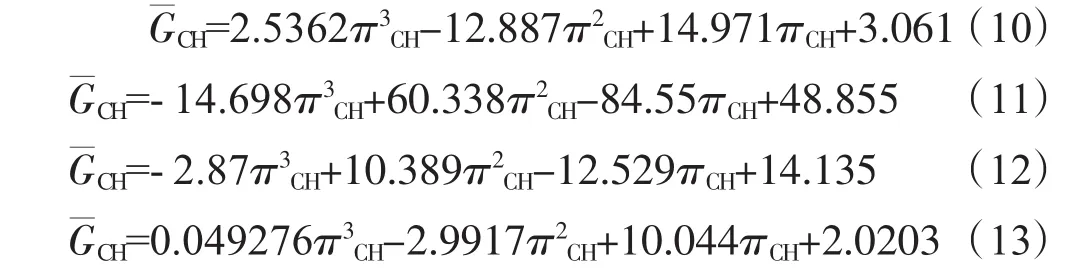
然后對式中的各項系數進行2次擬合，得到關于“壓比-折合轉速”之間的函數關系

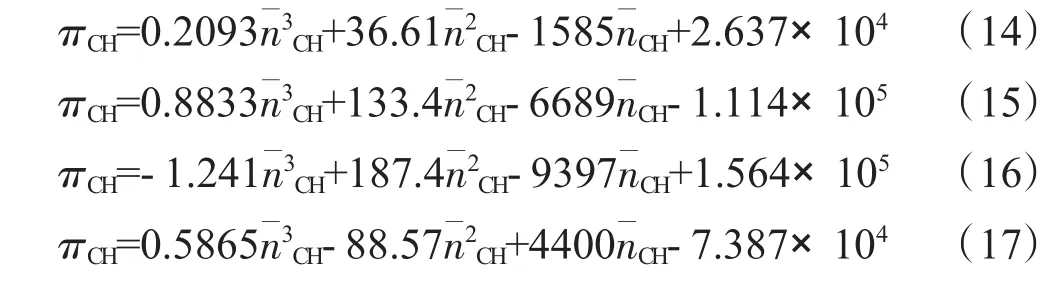
經過上述2步擬合之后，最終可以得到“折合流量-壓比-折合轉速”之間的函數關系式

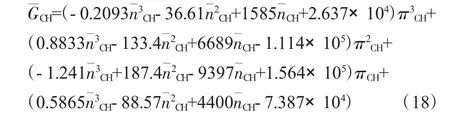
4 結論

本文將5個統計學擬合檢驗指標引入燃氣輪機部件特性方程的擬合過程中，通過實際算例分析得出了最佳的擬合次數。分析表明：所選擇的擬合次數能夠較好的對曲線的實際情況進行描述。得到擬合值與測量值的相對誤差為±0.2%，殘差范圍為±5×10-13，進一步證明了擬合誤差小，與曲線吻合度高。綜合應用上述檢驗指標所獲得的特性方程的最佳擬合次數具有可行性與可靠性。引入檢驗指標避免了在擬合過程中經驗化選擇擬合次數的問題，為特性曲線擬合次數從定性選擇過渡到定量計算提供了1條可行之路。

[1]周密.基于信息融合技術的燃氣輪機氣路故障診斷研究[D].武漢：海軍工程大學，2009.

[2]Lee T M，Lee E K，Yang M Y.Precise bi-arc curve fitting algorithm for machining an aspheric surface[J].International Journal of Advanced Manufacturing Technology，2007，31（11-12）：1191-1197.

[3]賀星.基于熱力學功勢的燃氣輪機性能退化研究[D].武漢：海軍工程大學,2010.

[4]袁萃，楊青真，陳立海.飛行器特性曲線擬合與飛行仿真研究[J].計算機仿真，2008，25（2）：53-57.

[5]方前.航空發動機系統建模與故障診斷研究[D].西安：西北工業大學，2005.

[6]Verboven P，Guillaume P，Cauberghe B. Multivariable frequency-response curve fitting with application to modal parameter estimation[J].Automatic，2005，41 （10）：1773-1782.

[7]曾嶸.支持向量機在設備故障診斷中的應用研究 [D].長沙：中南大學，2007.

[8]劉喜超，唐勝利.基于偏最小二乘法的壓氣機特性曲線的擬合[J].汽輪機技術，2006，48（5）：327-329.

[9]Suk B Y，Widodo A.Support vector machine for machine fault diagnosis and prognosis[J].Journal of System Design and Dynamics.2008，2（1）：12-23.

[10]趙世榮.航空發動機自適應建模及故障診斷[D].南京：南京航空航天大學，2007.

[11]翁史烈.燃氣輪機性能分析 [M].上海：上海交通大學出版社，1987.

[12]劉永葆.艦用燃氣輪機 [M].武漢：海軍工程大學出版社，2007.