基于TDC的GPS馴服恒溫晶振系統(tǒng)設(shè)計

陸加海,張同雙,陶小紅,陳浩謙,李春海

(1.上海交通大學(xué),上海200030;2.中國衛(wèi)星海上測控部,江蘇江陰 214431)

1 引 言

測控系統(tǒng)要求有高精度的時間頻率系統(tǒng)。為了保持站點(diǎn)間時間同步,一般采用銣原子鐘或恒溫晶振(Oven-Controlled Crystal Oscillator,OCXO)來提供時間頻率信號。前者的成本較高,后者頻率準(zhǔn)確度較差,不能滿足測控系統(tǒng)的指標(biāo)要求。

為解決上述問題,本文采用GPS對恒溫晶振進(jìn)行馴服,綜合了GPS時間信號長穩(wěn)指標(biāo)高的優(yōu)點(diǎn)和恒溫晶振短穩(wěn)指標(biāo)高的優(yōu)點(diǎn),從而獲得了高穩(wěn)定度和高準(zhǔn)確度的頻率信號。

為了計算恒溫晶振相對于GPS的頻率偏差,需要長時間測量GPS秒信號與恒溫晶振分頻信號之間的時差,通過時差計算得到頻率偏差,再根據(jù)頻率偏差來校準(zhǔn)恒溫晶振,所以時差測量的精度直接影響到頻率馴服的精度。文獻(xiàn)[1]采用FGPA延遲線內(nèi)插法測時差,測量精度達(dá)到121 ps,但測量線性化較差、成本高。文獻(xiàn)[2]介紹了模擬內(nèi)插法測時差,測量精度達(dá)到400 ps,但易受噪聲干擾、實(shí)現(xiàn)困難;

本文采用時間數(shù)字轉(zhuǎn)換器(Time to Digital Converter,TDC)測量時差,精度達(dá)到250 ps,極大減小了測量誤差,且設(shè)計簡單、成本低,有效實(shí)現(xiàn)了GPS馴服恒溫晶振系統(tǒng)的設(shè)計。

2 系統(tǒng)設(shè)計

2.1 系統(tǒng)硬件組成

系統(tǒng)組成框圖如圖1所示,主要由GPS模塊、TDC時間數(shù)字轉(zhuǎn)換器、分頻模塊、數(shù)據(jù)處理單元、D/A轉(zhuǎn)換模塊和恒溫晶振等組成。GPS模塊用于輸出標(biāo)準(zhǔn)的GPS秒脈沖信號,分頻模塊將恒溫晶振頻率信號分頻成1 PPS信號送TDC模塊,TDC模塊用于測量恒溫晶振分頻1 PPS信號與GPS秒信號之間的時差,數(shù)據(jù)處理單元對時差數(shù)據(jù)進(jìn)行處理后得到恒溫晶振相對于GPS的頻率偏差,并控制D/A轉(zhuǎn)換模塊對恒溫晶振進(jìn)行頻率修正。

圖1 系統(tǒng)組成框圖Fig.1 Block diagram of the system

2.2 時差測量電路設(shè)計

TDC是時間數(shù)字轉(zhuǎn)換器的英文縮寫。這類芯片把時差直接轉(zhuǎn)化為高精度的數(shù)字值。它們被描述為與ADC(模擬數(shù)字轉(zhuǎn)換器)功能相似的器件。通常TDC是用在分辨率小于1 ns的測量場合。本設(shè)計使用TDC-GP1芯片進(jìn)行測量,其測量電路框圖如圖2所示。將待測的GPS秒信號和晶振1 PPS信號送TDC模塊;START信號由分頻模塊產(chǎn)生并送TDC模塊,用于控制測量時序。TDC模塊將時差轉(zhuǎn)化為數(shù)字值送數(shù)據(jù)處理單元。

圖2 時差測量電路框圖Fig.2 Block diagram of time difference measurement circuit

時差在TDC模塊的測量時序如圖 3所示,將GPS秒信號與恒溫晶振分頻得到的1 PPS信號進(jìn)行比對,得到的時間間隔即是待測的時差。

圖3 時差測量時序圖Fig.3 Time difference measurement timing diagram

圖3中START信號為測試開始信號,GPS秒信號與晶振1 PPS信號之間的時間間隔T為待測的時差。信號脈沖寬度要求大于2.5 ns,開始信號與被測信號之間時間間隔要求大于3 ns、小于7.6 μ s。

為了保證每次被測信號落在允許的測量范圍內(nèi)。測量開始之前應(yīng)進(jìn)行初步的時間同步,確保GPS秒與晶振1 PPS之間的時差小于3 μ s。START信號通過將GPS秒延時約999 996 μ s后產(chǎn)生,確保START信號與GPS秒信號之間的時差保持在4 μ s左右。

2.3 分頻模塊的設(shè)計

分頻模塊采用CPLD設(shè)計實(shí)現(xiàn),通過CPLD分頻計數(shù)將恒溫晶振的10 MHz頻率信號分頻為1 PPS信號,同時將 GPS秒延時999 996 μ s后生成 START信號,確保START信號超前GPS秒信號4 μ s。當(dāng)晶振1 PPS與GPS秒之間的時差大于3 μ s時通過計數(shù)器清零的方法進(jìn)行同步,確保兩者之間的時差小于3 μ s。其時序如圖4所示。

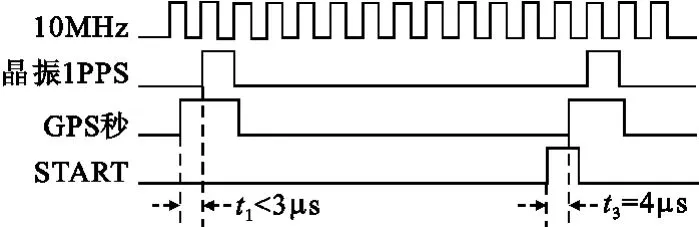
圖4 分頻模塊時序圖Fig.4 Timing diagram of frequency division module

3 數(shù)據(jù)處理

根據(jù)頻率和周期互為倒數(shù)的關(guān)系,可采用測時差的方法[4](以GPS的秒信號為參考)來測量本地頻率源的頻率準(zhǔn)確度(Δf/f),作為校頻的依據(jù)。計算公式如下:

按照公式(1)可以計算出恒溫晶振相對于GPS的頻率偏差[5],其中 Δt2、Δt1分別為 t2、t1時刻測得的晶振1 PPS與GPS秒之間的時差值。根據(jù)頻率偏差的大小,將需要調(diào)整的頻率偏差量轉(zhuǎn)換為模擬電壓施加在壓控恒溫晶振的電壓控制端,便可以實(shí)現(xiàn)對恒溫晶振進(jìn)行頻率修正。

但GPS信號在傳輸過程中存在各種干擾[3],這些干擾造成GPS輸出的秒信號存在一定的抖動,其短穩(wěn)較差。通過對時差值進(jìn)行遞推平均濾波可以有效消除GPS秒信號抖動的影響[6]。取測量得到的時差數(shù)據(jù) Δt1,Δt2,Δt3,…,Δtn,…,以 n 作為窗口長度對其中的n個測量值取平均,通過移動窗口得到新的時差數(shù)據(jù)序列[1]ΔT1,ΔT2,ΔT3,…,ΔTn,…,如公式(2)所示:

為了使頻率準(zhǔn)確度 Δf/f測量更準(zhǔn)確,對遞推平均濾波算法進(jìn)行優(yōu)化,取 ΔTj,ΔTn+j,ΔT2n+j,ΔT3n+j,…,ΔTmn+j,…,作為實(shí)際測量序列進(jìn)行計算,如公式(3)所示:

將式(2)代入式(3)得到

圖5是使用本系統(tǒng)測量得到的恒溫晶振相對于GPS系統(tǒng)的時差曲線,該曲線由于GPS秒信號抖動而存在一定的波動,使用這些數(shù)據(jù)計算得到的頻率偏差也會受到影響而發(fā)生波動,所以不能直接使用。圖6是添加遞推平均濾波處理后得到的時差數(shù)據(jù),其濾波窗口n設(shè)置為120。濾波后時差數(shù)據(jù)的抖動減小約兩個數(shù)量級。

圖5 時差數(shù)據(jù)濾波前曲線Fig.5 Curve before time difference data filtering

圖6 時差數(shù)據(jù)濾波后曲線Fig.6 Curve after time difference data filtering

頻率調(diào)節(jié)通過16位DAC(數(shù)字模擬轉(zhuǎn)換器)實(shí)現(xiàn),將需要調(diào)整的頻率偏差值轉(zhuǎn)換為模擬電壓,施加在恒溫晶振的控制電壓輸入端,實(shí)現(xiàn)對恒溫晶振頻率的調(diào)控。

4 試 驗(yàn)

本設(shè)計中采用MV180 OCXO雙層恒溫晶振,其頻率牽引范圍為±3×10-7,外部控制電壓范圍為0～+5 V。GPS模塊采用Motolora M12+,在位置保持模式下,輸出秒信號的抖動方差 σ<20 ns。時間數(shù)字轉(zhuǎn)換器使用TDC-GP1芯片,其測量精度達(dá)到250 ps,測量誤差遠(yuǎn)小于GPS秒信號抖動引入的誤差。16位數(shù)模轉(zhuǎn)換芯片采用DAC8571,其輸出電壓對恒溫晶振的理論頻率調(diào)諧靈敏度優(yōu)于1×10-11。圖7所示為根據(jù)濾波后的時差數(shù)據(jù)計算得到的頻率準(zhǔn)確度曲線。不采用濾波算法頻率馴服時間為數(shù)個小時,采用濾波算法后頻率馴服時間縮短為約1 200 s。實(shí)驗(yàn)表明,馴服后恒溫晶振的頻率準(zhǔn)確度優(yōu)于3×10-11。

圖7 馴服后頻率準(zhǔn)確度曲線Fig.7 Tamed frequency accuracy curve

5 小 結(jié)

本文通過采用時間數(shù)字轉(zhuǎn)換器測量時差,簡化了GPS馴服恒溫晶振系統(tǒng)的硬件設(shè)計,測量精度達(dá)到250 ps,極大減小了測量誤差。設(shè)計了優(yōu)化的遞推平均濾波算法對時差數(shù)據(jù)進(jìn)行濾波處理,消除了GPS秒信號抖動引入的干擾,縮短了頻率馴服時間。頻率馴服時間約為1 200 s,與國內(nèi)同類應(yīng)用相比,縮短約一個數(shù)量級;頻率馴服精度優(yōu)于3×10-11。

[1]盧祥弘,陳儒軍,何展翔.基于FPGA的恒溫晶振頻率校準(zhǔn)系統(tǒng)的設(shè)計[J].電子技術(shù)應(yīng)用,2010(7):104-107.LU Xiang-hong,CHEN Ru-jun,HE Zhan-xiang.The designof frequency calibrationsystem for OCXO based onFPGA[J].Measurement Control Technology and Instruments,2010(7):104-107.(in Chinese)

[2]孫杰,潘繼飛.高精度時間間隔測量方法綜述[J].計算機(jī)測量與控制,2007,15(2):145-148.SUN Jie,PAN Ji-fei.Methods of High Precision Time-Interval Measurement[J].Computer Measurement&Control,2007,15(2):145-148.(in Chinese)

[3]單慶曉,楊俊.衛(wèi)星馴服時鐘系統(tǒng)的新進(jìn)展[J].測試技術(shù)學(xué)報,2009,23(5):396-401.SHAN Qing-xiao,YANG Jun.Review of Satellite Disciplined Clock System[J].Journal of Test and Measurement Technology,2009,23(5):396-401.(in Chinese)

[4]楊旭海,翟惠生,胡永輝,等.基于新校頻算法的GPS可馴銣鐘系統(tǒng)研究[J].儀器儀表學(xué)報,2005,26(1):41-44.YANG Xu-hai,ZHAI Hui-sheng,HU Yong-hui,et al.Study on GPS Disciplined Rb Clock Based on New Frequency Accuracy Measurement Algorithm[J].Chinese Journal of Scientific Instrument,2005,26(1):41-44.(in Chinese)

[5]ValdesM D,Villares IFarina J,Moure M J.A FPGA-based frequency measurement system for high—accuracy QCM sensors[J].Industrial Electronics,2008,34(11):1707-1712.

[6]Cadenas O,Megson G.Pipelining considerations for an FPGA case[C]//Proceedings of 2001IEEE International Symposium on Digital Systems Design.Warsaw,Poland:IEEE,2001:276-283.