應用ANSYS實現幾何非線性分析方法

陳學玲

（黑龍江交通職業技術學院，黑龍江 齊齊哈爾 161002）

應用ANSYS實現幾何非線性分析方法

陳學玲

（黑龍江交通職業技術學院，黑龍江 齊齊哈爾 161002）

本文簡要介紹了用ANSYS對桿系結構進行非線性分析時應當注意的問題及方法。通過Williams雙桿體系這個算例來介紹幾何非線性全過程分析，表明ANSYS軟件豐富的單元庫、強大的求解器以及便捷的后處理功能，對工程結構進行非線性分析不失為一種很好的方法。

桿系結構；幾何非線性 ANSYS；全過程分析BEAM3

對于許多工程問題，結構的剛度是變化的，必須用非線性理論解決，而幾何非線問題就是非線性理論中的一類。因幾何變形引起的結構剛度變化的一類問題都屬于幾何非線性問題。幾何非線性理論一般可以分成大位移小應變即有限位移理論和大位移大應變理論即有限應變理論。其核心是由于結構的幾何形狀或位置的改變引起結構剛度矩陣發生變化，也就是結構的平衡方程必須建立在變形后的位置上。ANSYS程序充分考慮了這兩種理論。ANSYS所考慮的幾何非線性通常分為3類：①大應變，即認為應變不再是有限的，結構本身的形狀可以發生變化，結構的位移和轉動可以是任意大小；②大位移，即結構發生了大的剛體轉動，但其應變可以按照線性理論來計算，結構本身形狀的改變可以忽略不計；③應力剛化，是指單元較大的應變使得單元在某個面內具有較大的應力狀態，從而顯著影響面外的剛度。

大應變包括大位移和應力剛化，此時應變不再是“小應變”，而是有限應變或“大應變”；大位移包括了其自身和應力剛化效應，但假定為“小應變”；應力剛化被激活時，程序計算應力剛度矩陣并將其添加到結構剛度矩陣中，應力剛度矩陣僅是應力和幾何的函數，因此又稱為“幾何剛度”。

幾何非線性問題一般指的是大位移問題，只有在材料發生塑性變形時，以及類似橡皮這樣的材料才會遇到的大的應變，大變形一般包含大應變、大位移和應力剛化，而不加區分。

1 幾何非線性分析應注意的問題

用ANSYS進行幾何非線性分析時，首先要打開大位移選項，即（NLGEOM，ON），并設置求解控制選項，可根據問題類型而定。其次是模型修正問題或缺陷問題，在大多數實際問題分析中，該項可根據實際結構修正模型，或不修正模型也可直接進行計算分析。但對于理想柱、梁側傾的非線性分析，則必須進行模型修正（可采用實際缺陷或采用ANSYS設置），否則無法進行非線性分析。

ANSYS采用工程應變和工程應力，對數應變和真實應力，Green－Lagrange應變和第二Piola－Kirchoff應力3種應變和應力。具體采用何種應變和應力，程序根據分析類型和采用的單元自動選擇。

在大應變分析的任何迭代中，大的縱橫比，過度的頂角以及具有負面積的已扭曲單元都是有害的。因此，必須注意單元已扭曲的形狀。如果已扭曲的網格是不能接受的，可以人工改變開始網格，以產生合理的最終結果見圖1。

某些單元支持大的轉動，但不支持大的形狀改變。在一個大撓度分析中，單元的轉動可以任意地大，但是應變假定是小應變。在所有梁單元以及除了LINK11單元的所有桿單元都具有大撓度效應。通過打開NLGEOM命令來激活撓度效應。

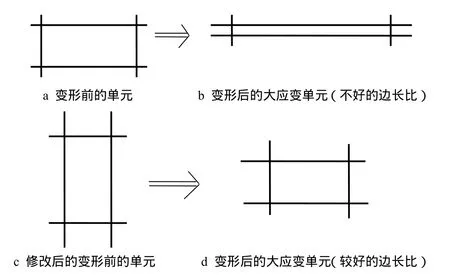
圖1 在大應變分析中避免低劣單元形狀的發展具有小應變的大偏移

在大變形分析中（NLGEOM，ON）包含應力剛化效應（SSTIF，ON），這時，把應力剛度矩陣加到主剛度矩陣上以在具有大應變或大撓度性能的大多數單元中產生一個“近似的”協調切向剛度矩陣。BEAM4和SHELL63是通過設置KEYOPT（2）=1和NLGEOM，ON在初始求解前激活應力剛化。當大變形效應打開時，這個KEYOPT設置激活一個協調切向剛度矩陣選項。當協調切向剛度矩陣被激活時，也就是當KEYOPT（2）=1且NLGEOM，ON時，SSTIF，ON對BEAM4和SHELL63將不起作用。

對于桿、梁和殼單元，在大撓度分析中通常應使用應力剛化。在應用這些單元進行非線性分析時，只有當打開應力剛化時才得到精確的解。但當用桿、梁或殼單元來模擬剛性連桿，耦合端或者結構剛度有大的變化時不應使用應力剛化。

網格密度對收斂有較大影響，同時影響結果的正確性，應進行靈敏度分析。

避免單點集中力和單點約束以及“過約束條件”等。

在大變形分析中，節點坐標系不隨變形更新，因此節點結果均以原始節點坐標系列出。但是多數單元坐標系跟隨單元變形，因此單元應力或應變會隨單元坐標系而轉動。

采用合適的計算方法，對于一般的幾何非線性分析可以采用牛頓－辛普森法，但對于結構的剛度發生突然的變化，或者說結構剛度變化較大的情況，應采用弧長法，此外還必須合理的配置荷載步和荷載子步。

2 幾何非線性全過程分析

圖2 雙桿體系荷載－位移曲線

結構條件不變而僅考慮某個加載過程中結構隨時間的力學響應，叫做全過程分析，本節通過Williams雙桿體系這個算例來介紹幾何非線性全過程分析。

圖2表示一個由兩個梁單元組成的平面剛架，該結構具有較高的幾何非線性。最初Williams從理論和實驗兩方面研究了該結構的非線性性能。后來Wood和Zienkiewicz則用有限元法對該結構做了計算分析，計算中每半跨結構取為五個單元，沈世釗用SNAP程序對此剛架也進行了分析。

本文用ANSYS對此結構進行模擬。采用BEAM3單元，每個桿件劃分為5個單元，打開弧長法。并采用缺省的弧長控制選項，荷載子步為100，計算結果見圖2。

圖2中的荷載－位移曲線Williams的試驗結構和Wood等的有限元分析結果以及和沈世釗用SNAP程序算得的結果十分接近。

3 結束語

從上文的分析中可以看出，用ANSYS對桿系結構進行幾何非線性數值分析十分優越。因為ANSYS軟件具有豐富的單元庫、強大的求解器以及便捷的后處理功能，用其對工程結構進行非線性分析不失為一種很好的方法

1 王新敏.ANSYS工程結構數值分析［M］.北京：人民交通出版社，2007：346～365

2 F S WILLIANS．An Approach to the Nonlinear Behaviour of the Members of a Rigid Jointed plane Framework with Finite Element Deflections. Quart.［J］. Mech.Appl.Math. Val 17, 1964:451～469

3 R D WOOD and O.C.ZIENKIEWICZZ. Geometrically Nonlinear Finite Element Analysis of Beams, Frames, Arches and Axisymmetric Shells Computand Struct［J］. Vol.7, 1977:725～735

4 沈世釗.網殼結構穩定性［M］北京：科學出版社，1998：37～39

The Method of Analysing Geometrical Nonlinearity by ANSYS

Chen Xueling

The problem and methods of using ANSYS to analyse geometrical nonlinearity is introduced briefly. The Williams double－rod system is used for example to introduce the geometric nonlinear analysis, show that the ANSYS software have rich of cell libraries and powerful solver and convenient post－processing. ANSYS is a good method to analyse the geometric nonlinear of engineering structures.

frame structures; geometrical nonlinearity; ANSYS; full－range analysis ;BEAM3

U445

A

1000－8136（2011）06－0134－02