分離變量法在靜電場問題中的應用

張保花 郭福強 李艷青

(1,2,3.昌吉學院物理系 新疆 昌吉 831100)

1 引言

靜電場問題是電動力學的核心問題[1]，是繼電磁學理論之后的重要理論知識。利用電磁學所學知識對一些實際問題不能解決，而電動力學是在人類對電磁現象的長期觀察和生產活動中發展起來的，對解決實際問題起到了十分重要的作用。本論文就是把電磁場的基本理論應用到實際情況，其研究的主要問題是：在給定的自由電荷分布以及周圍空間中存在介質或導體分布的情況下，怎樣求解靜電場問題，主要介紹利用分離變量法求解靜電場的一般步驟，并在不同的環境下分離變量法對邊界條件和邊值關系的適當選擇。

2 分離變量法求解的方程及通解

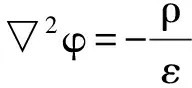
▽2φ=0

(1)

上式稱為拉普拉斯方程(拉氏方程)。產生電場的電荷都分布于區域V的邊界上，它們的作用通過邊界條件反應出來。因此，這類問題的解法是求拉普拉斯方程的滿足邊界條件的解，(1)式的通解可以用分離變量法給出。

先根據界面形狀選擇適當的坐標系，然后在該坐標系中用分離變量法解拉普拉斯方程。最常用的坐標系有球坐標系和柱坐標系[3]。這里寫出用球坐標系中軸對稱情形下拉普拉斯方程的通解形式。

在球坐標系下，球坐標用(R,θ,φ) 表示，R為半徑，θ為極角，φ為方位角，則拉氏方程在球坐標系中的通解為：

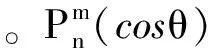
(3)

Pn(cosθ)為勒讓德函數，an和bn是任意常數，由邊界條件或邊值關系確定。所以，在每一個沒有電荷分布的區域內，φ滿足拉普拉斯方程，其通解已有(2)或(3)式給出，剩下的問題就是由具體的邊界條件或邊值關系確定這些通解中所含的任意常數，從而得到滿足邊界條件下的特解。

3 分離變量法的一般解題步驟

從分離變量法求解的方程及通解中，可以總結出分離變量法的一般解題步驟：

首先，當所求區域中的電荷密度ρ=0時，自由電荷只分布在某些介質或導體表面上，將這些表面視為區域邊界，并且電勢φ滿足 ▽2φ=0，則可以用分離變量法求解拉普拉斯方程；

其次，對實際情況分析，滿足球對稱或軸對稱，寫出相應的拉普拉斯方程通解；

再次，從實際情況出發，依次找出邊界條件和邊值關系來確定通解中的待定系數。

概括起來，大致有以下幾種類型的邊界條件[4]：

(1) 兩種絕緣介質界面上，邊值關系為

φ1=φ2

應用這條件可以把界面兩邊的電勢銜接起來。

(2)給出導體上的電勢，導體面上邊界條件為

φ=φ0(給定常數)

(3)給出導體所帶總電荷Q，在導體面上的邊界條件為

φ=常數 (待定)

應用上述邊界條件可以唯一地解出靜電場，用導體面上的另一邊界條件

可以得出導體面上的自由電荷面密度σ。

對于介質和導體存在的邊值關系：

(1)兩介質交接面上邊值關系

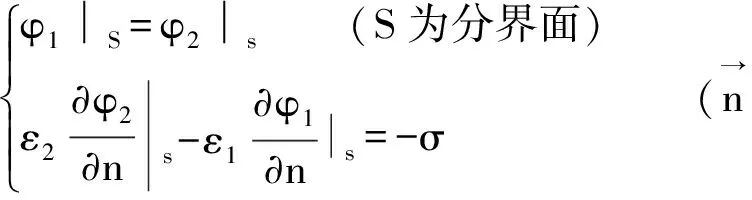
(2)導體表面上的邊值關系

由于導體表面為等勢面，因此在導體表面上電勢為常數。將介質情況下的邊值關系用到介質與導體的分界面上，并考慮導體內部電場為零，則可以得到第二個邊值關系：

4 分離變量法的實際應用

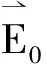
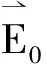
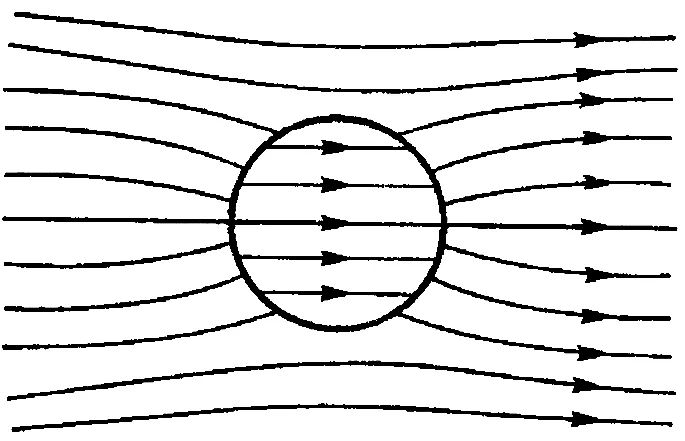
介質球的存在使空間分為兩均勻區域—球外區域和球內區域。兩區域內部都沒有自由電荷，因此電勢都滿足拉普拉斯方程。以φ1代表球外區域的電勢，φ2代表球內區域的電勢。由(3)式，兩區域的通解均為：

(4)

(5)

an,bn，cn和dn是待定常數。

邊界條件包括：

φ1→-E0Rcosθ=-E0RP1(cosθ)

(6)

因而 (a1=-E0,an=0(n≠1)

(7)

(2)R=0處， φ2應為有限值，因此 dn=0 ；

(8)

把 (4)和(5)式代入(8)式得

(9)

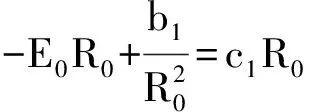
(10)

比較(9)式其它Pn項的系數可解出 bn=cn=0,n≠1 (12)

所有常數已經定出，因此本問題的解為

(13)

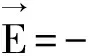
總之，通過以上例題求解了靜電場，使學生們更容易掌握在求解靜電場問題時分離變量法的解題步驟，以及在不同情況下靜電場所滿足的邊值關系及邊界條件[6]，學生們比較輕松的學習了靜電場的求解問題，記憶更加深刻，能夠更準確、更熟練地應用于解決實際問題。

參考文獻：

[1]郭碩鴻.電動力學(第三版)[M].高等教育出版社，2008.

[2]郭勁.鏡像法在靜電場和靜磁場的比較[J].高教研究，2000，(3)：31-33.

[3]尹真.電動力學(第二版)[M].科學出版社，2006.

[4]陳世民.電動力學簡明教程[M].高等教育出版社，2004.

[5]鄭春開.電動力學解題指導[M].北京大學出版社，2004.

[6]俞允強.電動力學簡明教程[M].北京大學出版社2003.