金融風險管理M-V方法的資產組合靈敏度分析

吳勛，徐永春

（1．西安石油大學經濟管理學院，西安710065；2．北京天相投資顧問有限公司，北京100140）

金融風險管理M-V方法的資產組合靈敏度分析

吳勛1，徐永春2

（1．西安石油大學經濟管理學院，西安710065；2．北京天相投資顧問有限公司，北京100140）

文章基于均值－方差（M-V）風險計量技術，分析了資產組合在資產品種減少的敏感性，通過引入協方差擾動，建立相關的M-V組合模型。同時和原模型進行比較，分析有效前沿的變化，探究其經濟意義。

M-V；投資組合；有效前沿

0 引言

投資者在構建投資組合時，不同的投資者有著不同的期望，通常理性投資者會選擇在持有期內風險最小的投資組合。但是由于收益與風險的隨機性，投資偏好的時變性，投資者需要經常調整所選擇資產的類別和數目，那么就面臨這樣一個問題：淘汰什么樣的資產，吸收那些資產，才能使投資收益達到最理想的狀態，因此研究關于資產數量變化情況下M-V資產組合有效前沿特征的靈敏度問題，將有著重要的理論和現實意義。因此本文就市場不存在無風險收益資產且允許賣空的條件下，研究資產數減少的情況下M-V投資組合有效前沿的漂移問題，探究其經濟意義。

1 M-V投資組合模型

假設t0時刻市場上n種資產，且組成的投資組合為x=為投資組合集

n)}。收益率為ri(i=1,2,…，n)，收益率的協方差Vn是正定對稱矩陣分別表示投資組合的期望收益率和方差。并假設：(1）不存在無風險收益資產，且允許賣空；

(2）n種資產具有線性不相關的收益特征，即任一資產的收益均不能表示為其余n-1個資產收益的線性組合；

(3）每種資產的期望收益率不完全相等。

t0時刻最優資產組合選擇問題可由下面模型來描述：

這里In表示n個分量均為1的n維列向量，Rn=(E(r1),E (r2),…，E(n))T是資產收益率的均值向量。由文獻[1]可得最小方差投資權重為：

式中

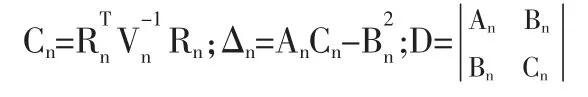
在(σ,μ)坐標系下該方程表示一條雙曲線，最小方差資產組合為該雙曲線的右支，而有效前沿為其右支的上半部分。全局最小方差資產組合為雙曲線右支的頂點，其期望收益率與風險分別為：

2 M-V投資組合前沿對資產數量減少的敏感性

假定t時刻資產種類減少到n-1種，假設淘汰了第n種資產，剩下的n-1種資產相關性結構必然會產生影響，現考慮由于減少一種資產后投資組合前沿曲線的變化的特征。

假設淘汰的第n種資產對協方差矩陣Vn-1中的元素σij影響程度為εij，εij為擾動因子，受到擾動后的協方差Vn-1可表示成正定矩陣，記δT=(σn1,σn2,…，σn,n-1)，于是：

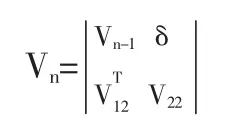
又有分塊矩陣求逆可得：

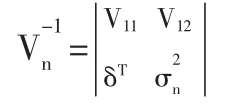
假設減少資產后，每種資產的期望收益率不完全相等，由文獻[2]得個風險資產所組成的新的投資組合集的有效前沿方程為：

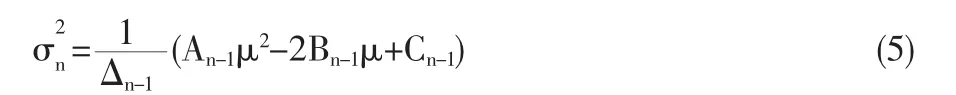
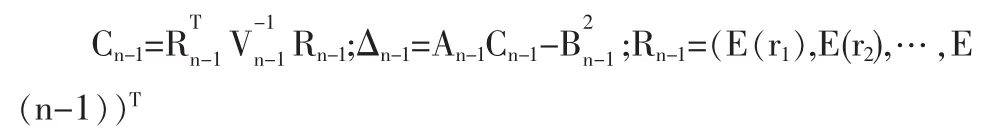
并且，由候為波（2000）等的結果，有效前沿曲線方程的系數有下面的遞推關系式成立：

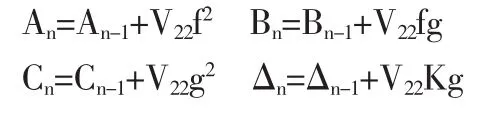
下面將f≠0與f=0兩種情形分別討論。這里f描述了所淘汰的資產與余下資產的協方差向量和協方差矩陣之間的關系。

由（3）、（5）和（6）可得

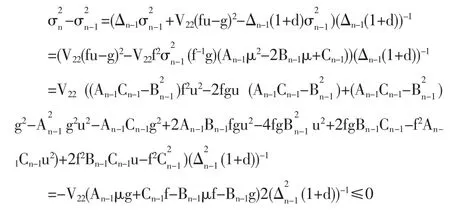
成立時，方差是嚴格增加的，即有效前沿將隨著資產數的減少向右移動。

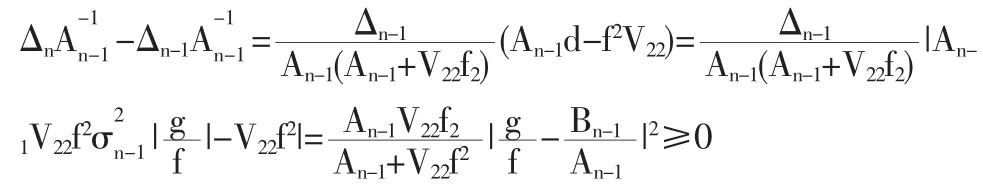
成立時，漸近線的斜率是嚴格減少的，即雙曲線張口變小，投資有效前沿向下移動，投資范圍變小，從而投資效益將有所損失。

當f=0時，有An=An-1，Bn=Bn-1，△n=△n-1+V22An-1g2。此時全局最小方差資產組合的收益和方差均不改變。

若g=0，有Cn=Cn-1，△n=△n-1，這時第n種資產的減少對資產組合的有效前沿不產生影響（這樣的資產稱為相對無效資產，否則稱為有效資產，它是相對某一資產而言的，此處是相對前n-1種資產而言的）。

若g≠0時，由△n=△n-1+V22An-1g2可得：

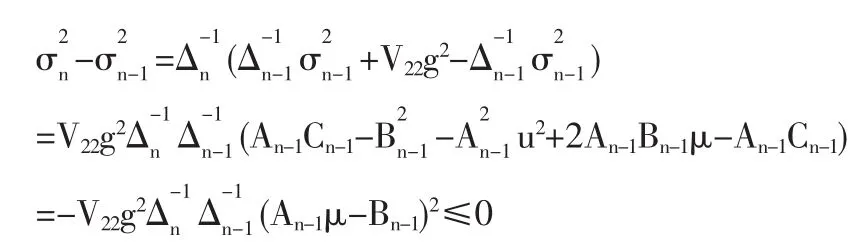
條件（7）和（8）是判別有效前沿移動方向的依據，并有下面定理。

定理1 如果f2+g2≠0，則條件（2.3）與（2.4）中至少有一個成立。

證明：用反證法，令（2.3）與（2.4）均不成立。由f2+g2≠0知f和g中至少一個不為零，設f≠0，則由（2.4）不成立得fBn-1-gAn-1=0，Bn-1gAn-1/f由（2.3）不成立得An-1μg+Cn-1f-Bn-1μf-Bn-1g=0，將Bn-1=gAn-1/f代入上式得Cn-1f-An-1f-1g2=0，進而有Cn-1= An-1f-2g2，由此可得同△n-1>0矛盾。從這個定理可知，若則與△n/An≥△n-1/An-1至少有一個嚴格不等式，其經濟意義是：當f和g中至少一個不為零時，資產數量的減少對有效邊緣產生影響，或向右下移動，或雙曲線開口變小。

3 靈敏度分析在金融風險管理中的意義

本文基于M-V模型，在考慮協方差矩陣受到擾動情形下，研究了資產組合有效前沿的問題。在市場不存在無風險收益資產且允許賣空的條件下，得出了當f2+g2≠0時，資產數量的減少對有效邊緣產生實質影響，或向右下移動，或雙曲線開口變小的結論。這些分析有助于投資者更好的調整其投資資產集合，淘汰一些業績較差的資產，吸收一些較好的資產（所謂較差的資產就是那些存在與否對有效前沿幾乎不產生影響的資產），達到規避風險，取得更多收益的目的。

囿于篇幅，僅考慮了投資組合前沿曲線對資產數量減少的靈敏度分析，對資產數量增加的情形將另文闡述。但研究還有一些值得繼續進行的地方，一是考慮資產數目增加或減少時有效前沿問題，二是可以在組合中加入無風險資產。

[1]XueHonggang．Portfolio'sSensitivityAnalysiswithoutRiskless Asset[J]．Journal of Engineering Mathematics，2003，(6)．

[2]Jarrow R A，Maksimovic V，Ziemba W T．Finance[M]．Handbook in Operations Research and Management Science，North-Holland Elsevier，1995．

[3]高全勝，李選舉．基于的投資組合對資產變化的敏感性分析[J]．數量經濟技術經濟研究，2005，(6)．

[4]徐成賢．金融工程計算[M]．北京：科學出版社，2007．

[5]袁先智．金融風險管理的新挑戰及次貸危機的啟示[J]．管理評論，2009，（3）．

[6]史樹中．金融學中的數學[M]．北京：高等教育出版社，2006．

(責任編輯/亦民)

0211

A

1002－6487（2011）06－0081-02

全國教育科學“十一五”規劃項目（DFA060116）

吳勛（1978-），男，河南南陽人，博士，研究方向：風險控制方法。

徐永春（1978-），男，安徽蚌埠人，博士，研究方向：金融資產投資組合分析。