負相協樣本下總體分位數的經驗似然漸近性質的推斷
李乃醫,李永明
(1.廣東海洋大學理學院,廣東湛江524088;2.上饒師范學院數學與計算機學院,江西上饒334001)
負相協樣本下總體分位數的經驗似然漸近性質的推斷
李乃醫,李永明
(1.廣東海洋大學理學院,廣東湛江524088;2.上饒師范學院數學與計算機學院,江西上饒334001)
文章在強平穩負相協樣本下,利用分組經驗似然比方法,克服了傳統經驗似然方法的缺陷,所得到的漸近分布為標準的卡方分布,便于構造總體分位數的漸近置信區間。
強平穩;負相協;分組經驗似然;置信區間
0 引言
NA(Negative Associate)相依概念在可靠性理論、滲透理論和多元統計分析中有廣泛的應用。經驗似然是1988年最早由Owen[7][8]引入經驗似然,它是一種非參數推斷方法,類似于Bootstrap和隨機加權方法,但有所不同的是它在每個樣本點上所賦予的概率是帶有選擇余地的,在一些合理的約束條件下,描繪了支撐在樣本上的一個多元似然,而經驗似然比方法所構造置信區域就是此多元似然的一個等高區域。更值得一提的是經驗似然比置信區域具有保范圍性,它與被置信的總體特征具有同樣的范圍,這是其它方法所不能到達的。并且它的區域形狀完全由樣本決定,其覆蓋概率不比Bootstrap置信區域差。正是由于經驗似然與經典或現代的其它統計方法相比具有上述突出的優點。因此,該方法引起了國內外許多統計學家的興趣,并將這一方法應用到多種統計模型及各種領域。
在相依情形下,經驗似然方法研究剛剛開始,尤其在NA相依樣本下利用該方法研究成果甚少。到目前為止,在獨立樣本和混合樣本下對分位數進行了經驗似然方法研究。本文將嘗試在NA(負相協)相依樣本下,克服普通經驗似然方法的缺陷,重新借助分組經驗似然比方法,構造未知的分位數漸近置信區間。首先給出NA序列和強平穩概念。
定義1[1]稱隨機變量X1,X2,…,Xn(n≥2)是NA的,如果對于集合{1,2,…,n}的任何兩個不相交的非空子集A1和A2,都有
Cov(f1(Xi,i∈A1),f2(Xj,j∈A2))≤0
其中f1與f2是任何兩個使得協方差存在的對每個變量均非降(或非升)的函數。稱隨機變量序列{Xi,i∈N}是NA序列,如果對任何n≥2,隨機變量X1,X2,…,Xn(n≥2)都是NA(負相協)的。
定義2 隨機變量序列{Xn|n≥1}稱強平穩,若對任意自然數對(i,j),序列(Xi+1,…,Xi+j)與(X1,…,Xj)有相同分布,其中1≤j 對數經驗似然比為 這里s∈R1且滿足 條件: (1)X1,X2,…,Xn是強平穩NA樣本; 定理1若上述條件成立,則有 此處 由于A2和σ2未知,結果不便應用,為了彌補這一缺陷,利用分組經驗似然方法,重新構造經驗似然比以使其極限分布不含未知參數。 (注:關于條件(2)是研究NA序列,通常需要對協方差結構做出這一約束要求。) 定理2在定理1的條件下,進一步有以下假設成立: (2)Y2i-1=ξi/m,Y2i=ηi/m(1≤i≤g)。 其中 則有 其中λ∈R1,滿足 分組后經驗似然比R'(ξp)由下式決定 本文以下為了簡單起見,適當抽樣使n=2mg。文中常數c在不同的地方可以取不同的值。 引理1[9]設{Xn,n≥1}為NA序列;A1,A2,…,Am是集合{1,2,…,n}的兩兩不交的非空子集。記αi=#(Ai),即為Ai中的元素個數,如果fi:Rαi→R(i=1,2,…,m)是對每個變元都非降(或非升)的函數,則f1(Xj,j∈A1),…,fm(Xj,j∈Am)仍為NA變量。 引理3[3]設X1,X2,…,Xn為NA變量,對p≥2,有E|Xj|<∞,且EXj=0,j=1,…,n。記則存在僅與p有關的常數Cp>0,使得 引理4[2]設{Xi|i≥1}是強平穩NA序列,假定EX1=0,E|并且則有 引理5 設{Xi|i≥1}是強平穩NA序列,并且滿足 則有 其中 引理6[10]設{Xn,n∈N}是NA序列,數列{bn,n∈N}滿足且則s收斂于0。 引理7 設{Xn,n∈N}是同分布的NA序列,則有 引理8 設{Xi|i≥1}是同分布NA序列,則有 易得 從而可知0是集合{I{X1≤ξp}-p,1≤i≤n}所構成的凸包的內點,因此存在為正。 又因為 由拉格朗日乘子法,得唯一解 其中s∈R1,并滿足注意到: 令γi=s(I{Xi≤ξp}-p),s滿足h(s)=0,由(6)式及引理2知: 于是有 因此 再由引理4和引理7知: 由條件得J2=Op(1) 又由(6)和引理2得 其中c為某個正數,故有 綜合(9)~(11)式便得 類似前面的討論,只需證明 由拉格朗日乘子法得 其中λ∈R1,且滿足易得 從而有 接下證明 又由 利用引理8得 由(18)及(19)式得 又由 由引理5和(18)式得 又由(21)、(22)和(24)式得 由(23)式和Taylor展開式得 利用引理5及引理4,同樣討論得 由(24)式得 由(18)和(24)式得 從而得K3=Op(1),綜(25)~(28)式知 定理2結論中的漸近分布不僅為標準的卡方分布,且無需估計總體未知的方差和協方差。 利用定理2,當樣本n比較大時,我們可構造未知的分位數ξp的置信水平為1-α的漸近置信區域:1-α,其中Cα為分布的上α分位點,通常α取0.05或 0.01。另外,在其它相依情形,如在正相協樣本下,值得進一步深入研究。 [1]Joag-DevK,ProschanF.NegativeAssociationofRandom Variable with Application[J].Ann.Statist.,1983,11. [2]潘建敏.NA序列中心極限定理的收斂速度[J].應用概率統計,1997, 13(2). [3]楊善朝.隨機變量部分和的矩不等式[J].中國科學,A輯,2000,30(3). [4]張軍艦,王成名等,相依樣本情形下經驗似然比置信區間[J].高校應用數學學報,1999,(14). [5]Kitamura,Y.Empirical Likelihood Methods with Weakly Dependent Process[J].Ann.Statist.,1997,(25). [6]Lin,L.,Runchu,Z.Block Empirical Edulidean Likelihood for Weakly Dependent Process[J].Statist.Probab.lett,2001,(53). [7]Owen,A.B.Empirical Likelihood Ratio Confidence Intervals for a Single Function[J].Biometrika,1988,(75). [8]Owen,A,B.Empirical Likelihood Confidence Regions[J].Ann. Statist.,1990,(18). [9]Matula,P.A Note on the Almost Sure Convergence of Sum of NegativeDependentRandomVariables[J].Statist.Probab.lett,1992,(15). [10]萬成高.NA序列的大數定律及收斂速度[J].湖北大學學報(自然科學版),2004,(3). [11]秦永松,有偏模型中一類統計泛函的經驗似然估計及漸進性質[J].應用數學學報,1998,(3). [12]Owen,A.B.Empirical Likelihood for Linear Model[J].Ann.Statist, 1991,(4). [13]秦永松.部分線性模型參數的經驗似然比置信區域[J].應用概率統計,1999,(4). [14]Chen,S.X.EmpiricalLikelihoodIntervalsforNonparametric Density Estimation[J].Biometrika,1996,83. [15]Chen,S.X,Qin,Y.S.Coverage Accuracy of Confidence Intervals in Nonparametric Regression[J].Acta Mathematicae Applicate Sinica,English Series,2003,(19). [16]Chen,S.X,Hall,P.Smoothed Empirical Likelihood Confidence for Quantiles[J].Ann.Statist,1993,(21). [17]Chen,S.X,Wong,C M.Smoothed Block Empirical Likelihood for Quantiles of Weakly Dependent Processes[J].Statistica Sinica, 2009,(19). [18]Zhang,J.J.Empirical Likelihood for NA Series[J].Statist.Probab Lett,2006,(76). [19]于卓熙,王德輝,史寧中.NA誤差下部分線性模型的經驗似然推斷[J].系統科學與數學,2009,(4). [20]Zhu,L.X,Xue,L.G.Empirical Likelihood Confidence Regions in a Partially Linear Single-Index Model[J].Journal of the Royal Statistical Society Series B-Statistical Methodology,2006,(68). [21]Xue,L,G,Zhu,L,X.Empirical Likelihood for a Varying Coefficient Model with Longitudinal Data[J].Journal of the American Statistical Association,2007,(102). (責任編輯/亦民) O212.4 A 1002-6487(2011)06-0017-04 國家自然科學基金資助項目(11061029);廣東海洋大學自然科學研究資助項目(1012138;0612163) 李乃醫(1979-),男,江西九江人,碩士,講師,研究方向:數理統計。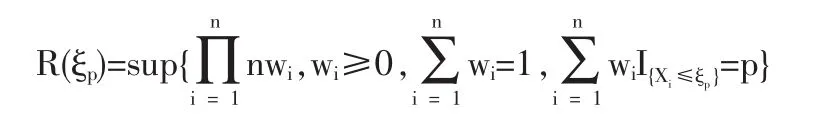
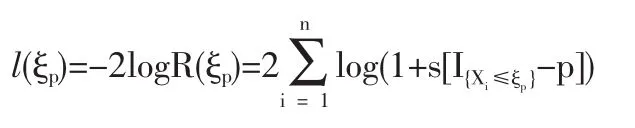
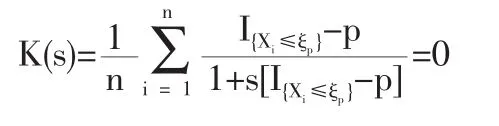
1 若干引理和定理
1.1 定理與引理
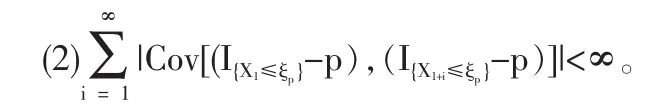
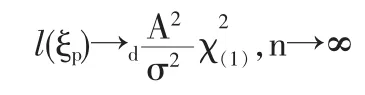
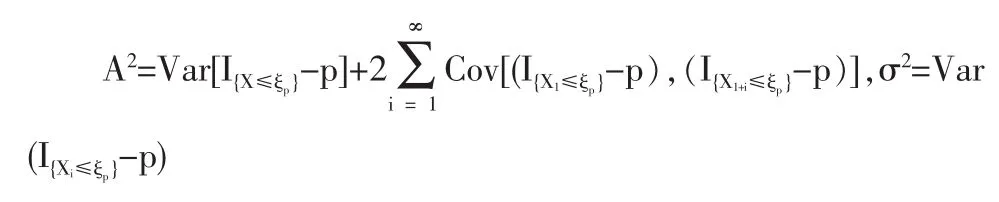
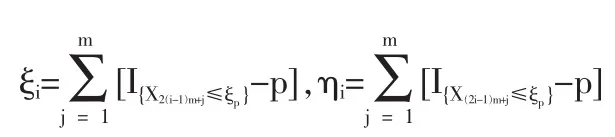
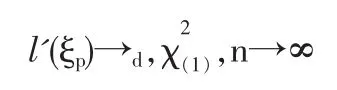
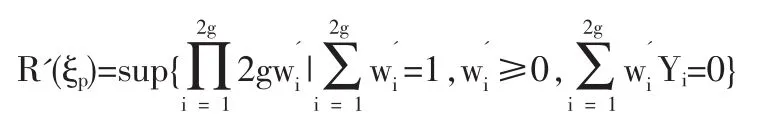
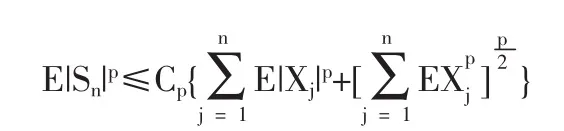

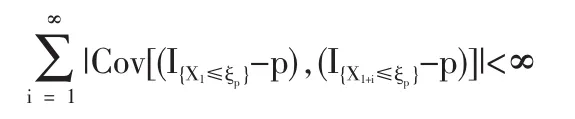
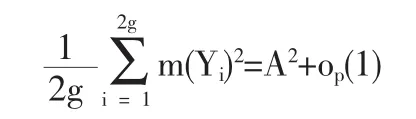
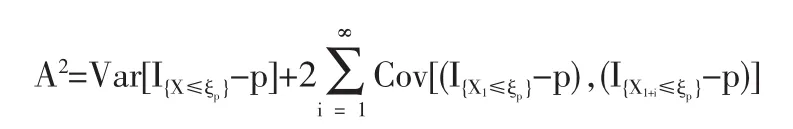
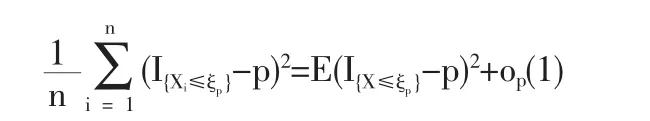
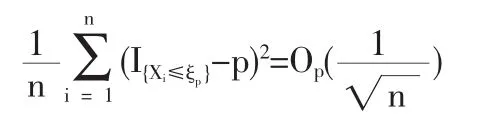
1.2 定理1的證明
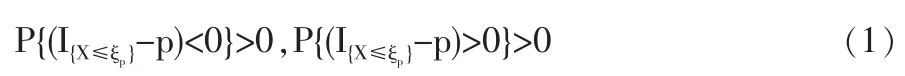

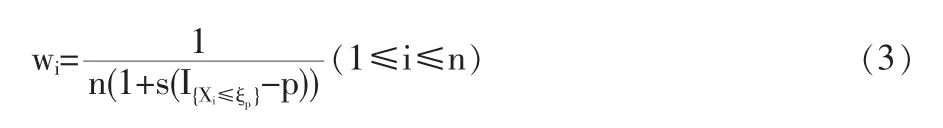
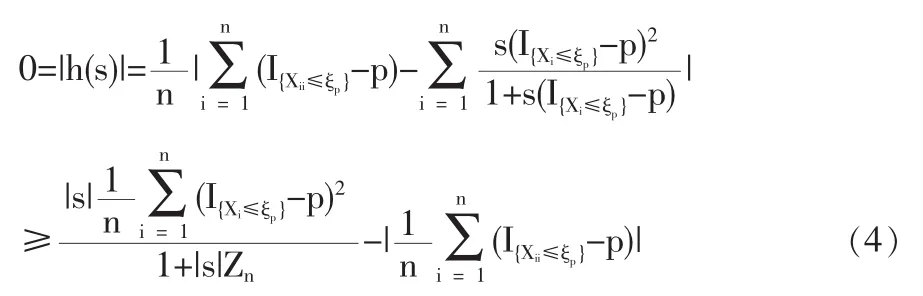

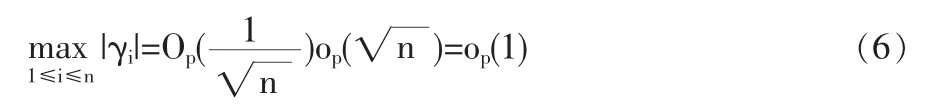
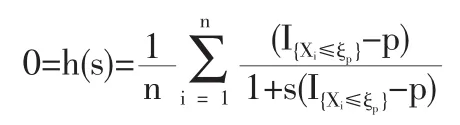
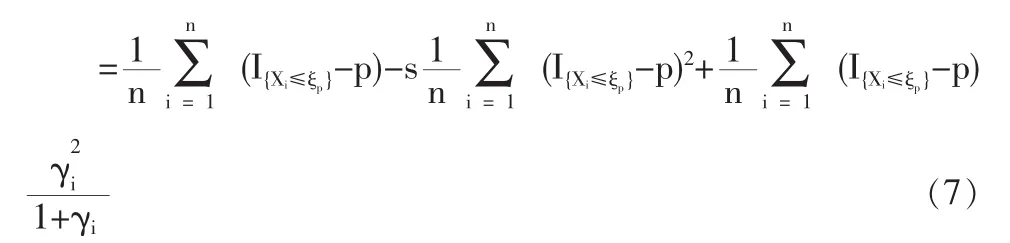
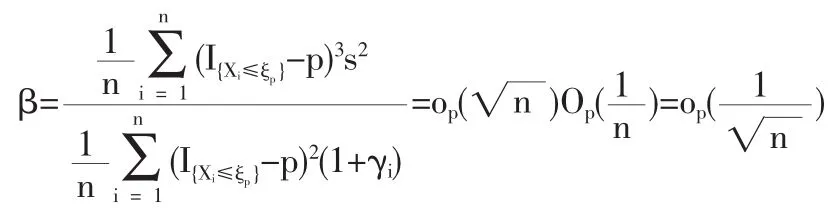
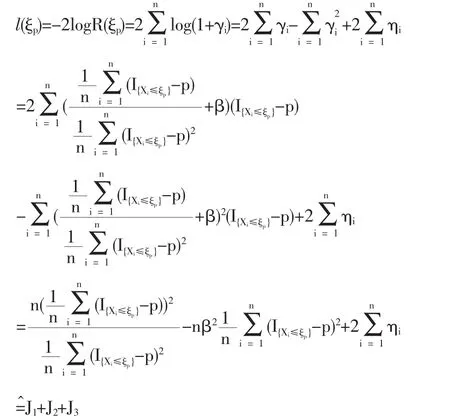

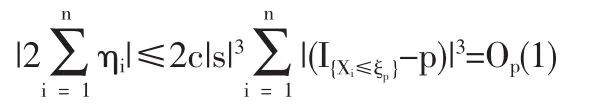


1.3 定理2的證明

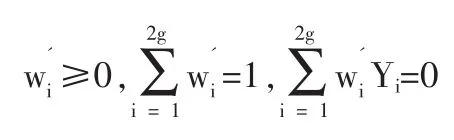
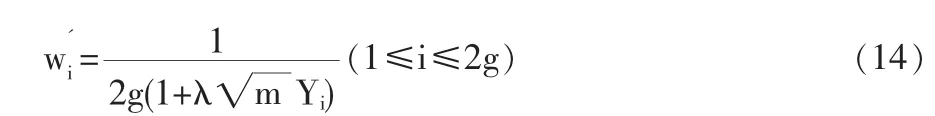
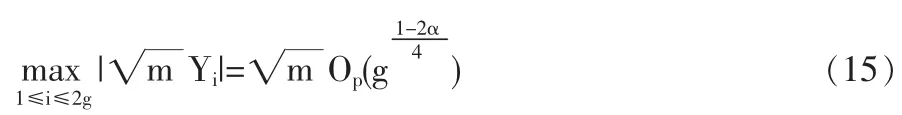
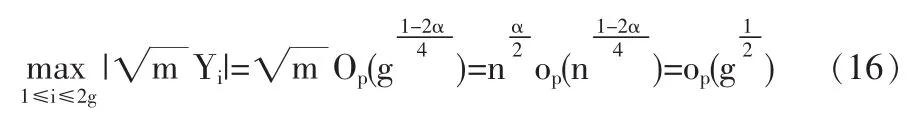

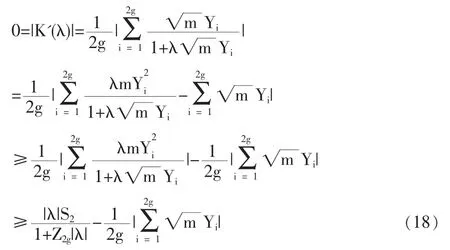
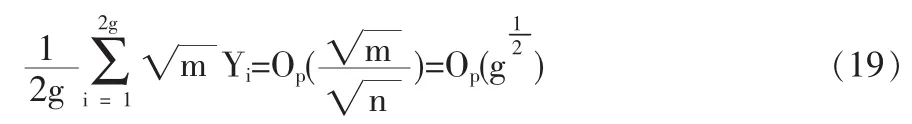

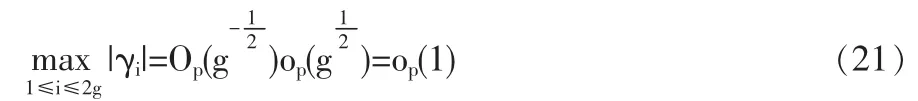
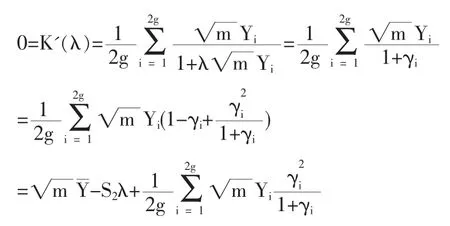

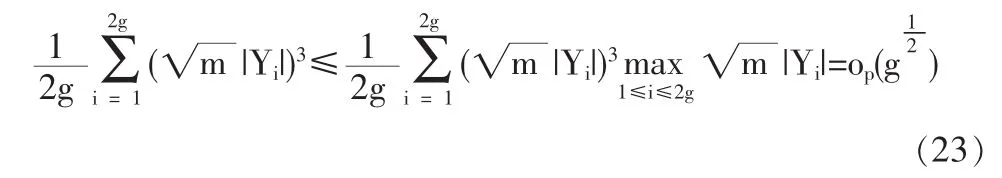
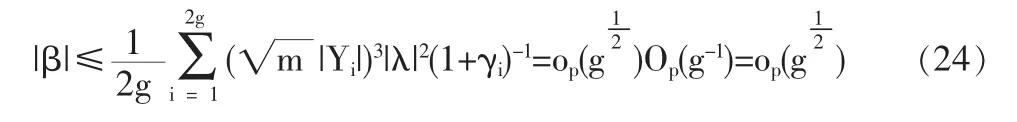
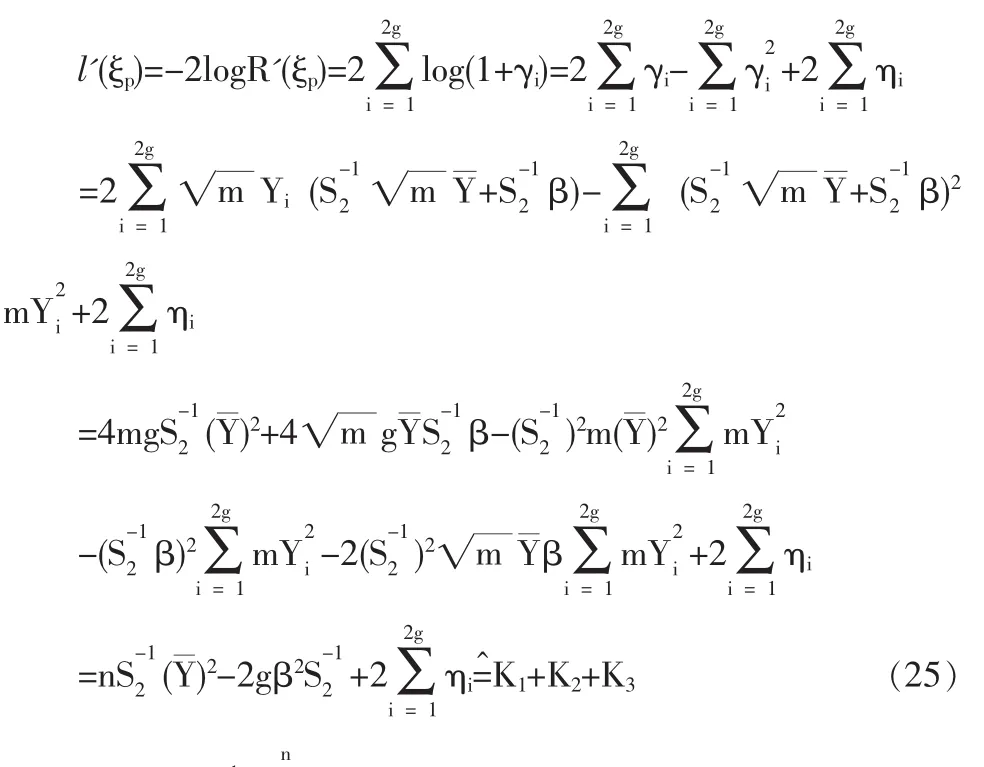


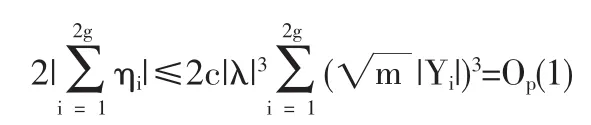

2 結論

