社會統計分析中的悖論與變換問題
程中興
(復旦大學社會學系,上海200433;廣西師范大學社會學系,桂林541004)
社會統計分析中的悖論與變換問題
程中興
(復旦大學社會學系,上海200433;廣西師范大學社會學系,桂林541004)
如何解釋隱現于列聯表中的辛普森悖論,如何區分回歸中logit變換與probit變換的內在差異與背后假定,是社會統計分析中兩大應用性問題。文章從社會統計對象的獨特特征出發,認為辛普森悖論與其說是“悖論”,不如說是反映了分類數據的非線性特征,反映了列聯表從高維壓縮至低維時的統計信息差異,實質上是歐氏空間的降維問題。同理,在回歸分析中,由于分類數據的非線性特征,無論logit變換,還是probit變換,實際上只有在0.2~0.8之間才基本呈現線性,在這個范圍之外,兩個函數都是高度非線性的。
辛普森悖論;分類數據非線性特征;logit變換;probit變換
0 引言
社會統計分析的數據絕大數是分類意義上的。它們要么是定性的定類、定序數據,要么是定量的離散數據[1],并不具備嚴格意義上的“+、-、×、÷”等數學運算特性[2]。
社會研究對象的這一“分類”特征,使得列聯表成為社會統計分析中應用最為廣泛的首選統計工具之一。因為列聯表是非參數的或僅要求很弱的參數(分布)假定。但在列聯表分析中,如何解釋隱現其中的辛普森悖論一直是一個重要問題。
此外,由于分類數據的非線性特征,回歸函數不可能是線性的,需要尋找一個鏈接函數,將分類變量的期望值變換成自變量的一個線性函數。然而,在實際應用中,logit變換與probit變換的內在差異與背后假定問題常為人們所忽視,進而影響了參數解釋。
1 辛普森悖論問題
辛普森悖論最早于1899年由卡爾·皮爾森(Karl Pearson)提出,但一直到1951年E.H.辛普森才正式描述并解釋這一現象,后來就以他的名字命名該悖論。關于辛普森悖論,國內學者關注不多,只有李思一(1984)、王軼豪(1986)、倪加勛(1992)、吳素萍(2000)、耿直(2000)、史希來(2006)、王健(2008)等人作過介紹性研究。
辛普森悖論是指,在分組比較中都占優勢的一方,在總體評價中卻并不占優勢。我們先來看一個源自真實生活的案例。1979年初,《美國歷史畫報》雜志對讀者類型和獲得期刊的方式進行了統計[3]。見表1。
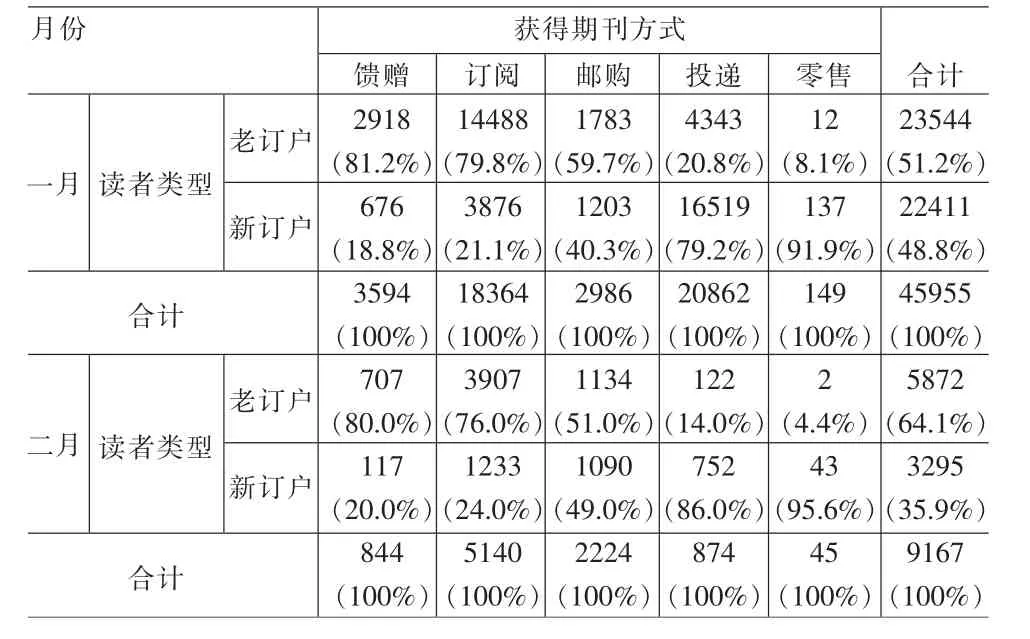
表1 《美國歷史畫報》統計
從表1可以看出,五種訂閱方式中,老訂戶1月份的續訂率要高于2月份,但合計后總的續訂率卻要低于2月份。除了上述案例外,還有其他很多真實的數據表現出了辛普森悖論現象,如Bickel等(1975),Wagner(1982),Neufeld(1995)。總之,辛普森悖論不是虛幻的,而是客觀存在的。問題是如何解釋辛普森悖論的產生原因。
由于統計的基礎在于概率,于是人們就從概率論加以解釋。辛普森悖論可定義為以下三種情況同時發生:
(1)P(I|A,B)>P(I|A,B');(2)P(I|A',B)>P(I|A'B');(3)P(I|B) 式(1)表示A在B下發生的概率大于A在B’下發生的概率。式(2)表示A’在B下發生的概率大于A在B’下發生的概率。式(3)表示B發生的概率小于B’發生的概率。 可以證明,如果保持試驗的結構相同,即P(A|B)=P(A|B')成立時,就可以避免辛普森悖論的出現(證明參見倪加勛,1992)。 雖然從概率角度可以詮釋辛普森悖論問題,但在筆者看來,這種詮釋具有柏拉圖“理念論”的色彩。因為這里遵從的是概率的頻率定義(列聯表中表征的是頻率),即 語文教師課堂主導地位的基石應該是教師對文本的理解和認識。我們要把握文本的定性解讀,但一個有一定教齡的語文教師應該警惕與文本對話環節的僵化少變,經典文本是常讀常新的。正如德國的接受理論先驅漢斯·羅伯特·姚斯所指出的,“一部文學作品,并不是一個自身獨立、向每一個時代的每個讀者均提供同樣觀點的客體,它不是一尊紀念碑,形而上學地展示其超時代的本質,它更多像一部管弦樂譜,在其演奏中不斷獲得讀者新的反響……使文本成為一種當代的存在。”我們應該在和文本對話的過程中賦予它超越時空的生命力,讓它成為一種“當代的存在”。 事實上,由于試驗或觀測次數N為∞是做不到的,因此,列聯表中的相對頻率只能說是對概率的一種柏拉圖意義上的“理念”摹本,近似到何種程度仍然是有疑問的。 如果從“現象”出發,就會發現:辛普森悖論與其說是悖論,不如說反映了社會統計分析對象的獨特特征,即分類數據的非線性特征。正是因為非線性,使得列聯表在不同的結構維度,表征了不可還原的不同統計信息。在上例中,由于將原始數據從三維結構壓縮成二維結構,自然就失去了另一維的信息,分析結構的不一致恰恰是不同維度統計信息的反映。因此,列聯表中的辛普森悖論實質上是一個將高維空間降到低維空間的產物[4]。 事實上,這種由于降維而丟失信息在其他統計分析方法中也會發生。例如,因子分析,雖然在理論上可以有無數個因子載荷矩陣,且每一個因子載荷矩陣對于一組潛在因子。但只有通過變換得出或組合出更合理、更便于解釋的潛在因子時,因子分析才可以說是成功的。整個分析過程實際上是一個歐氏空間降維和坐標變換(相當于坐標軸的剛性旋轉)的過程;又如,聚類分析,實際上是將分布在歐氏空間的觀測數據,投影到超橢球的方差最大方向和方差次大方向所形成的二維空間的平面上,然后按該平面上投影點之間的距離來直觀地劃分類別(相當于對應分析)。這也是一個歐氏空間的坐標變換和降維過程。 總之,列聯表在“高保真”地表征分類數據信息的同時,由于分類數據的非線性特征,在降維的過程中自然而然會帶來“辛普森悖論”問題。“辛普森悖論”的實質是“結構性”的,是不同列聯表結構維度的統計信息差異。 列聯表在本質上是對稱的。當社會統計分析的范圍拓展到不對稱的回歸分析時,考慮到因變量的分類屬性(categorical nature),回歸函數不可能是線性的,為此需要尋找一個鏈接函數(link functions),將分類變量的期望值變換成自變量的一個線性函數。在這里,有個常見的問題,即人們常常對鏈接函數logit與probit的內在差異與背后假定不做辨析,進而忽視這些差異與假定對于社會統計分析的參數解釋所具有的重要意義。 在回歸模型中納入分類變量作為自變量并不存在任何特別的難處,因為它主要涉及建立與自變量不同類別相對應的虛擬變量,所有已知回歸模型的性質都可以直接推廣到方差和協方差分析模型。但對于因變量是分類變量時,情況就徹底改變了,線性回歸的許多知識都無法簡單地加以運用。例如,對一個一二分因變量y,它的取值在[0,1]之間,一個自變量x,可以任意取值。我們知道,一個y對x的線性回歸意味著,x取任何值,預測線(predicted line)將不可避免地落在[0,1]之外,顯然這是不合理的。為此,我們需要尋找一個鏈接函數(link functions),將分類變量的期望值變換成自變量的一個線性函數。logit變換和probit變換就是其中最為典型的兩種變換。 先說logit變換。一般來說,logit變換可以解釋為成功對失敗之發生比率的對數。成功概率P的logit變換可以表示為: Probit變換是logit變換的一個替代選擇。用數學公式表示為: 從上式可以看出,logit和probit兩種分布函數的公式很相似,實際上,函數值相差也并不大,且都繞著p=0.5對稱(圖1)。 無論是probit變換,還是logit變換,在社會統計分析中并沒有實質上的理由確認哪一種更優。一些研究者基于中心極限定理往往傾向于probit變換,但在實際操作中,logit分布因概率分布和密度函數的簡單性而更受歡迎。 需要進一步指出的是,區分兩種變換的內在差異與背后假定是相當重要的: 首先,就分布來說,logit函數假設隨機變量服從邏輯概率分布,而probit函數則假設隨機變量服從正態分布。標準邏輯概率分布和標準正態分布的均值都為0,但方差不同,前者的方差為π2/3,后者的方差為0。這一差別進一步體現為logit模型的系數比可比的probit系數年要大。從理論上來講,一個probit模型系數大約乘以1.81就應當得到一個接近于logit系數的值。同理,logit估計值乘上大約0.55就可以得到一個近似的probit估計值。在實際操作中,有研究者建議以1.61和0.625作為乘數以得到更接近的近似值[7]。 其次,無論logit變換還是probit變換在0.2~0.8之間基本呈現線性。在這個范圍之外,兩個函數都是高度非線性的。這意味著,如果P被作為一個連續解釋變量(x)的函數進行統計建模,x對p的影響就不是常數,而會隨x的變化而變化。例如,我們發現當probit(pi)=logit(pi)=β0+β1xi=0時,x變化所帶來的變化比probit(pi)<0,logit(pi)<0或probit(pi)>0,logit(pi)> 0時要更大。這一點在對logit和probit系數進行解釋時要特別注意其特定的含義。 社會統計分析就其對象的數學形式來說與其他統計分析并無差異,都可用統一的矩陣表示: 但由于社會統計分析的數據絕大數是分類意義上的,使得列聯表分析、尋找鏈接函數成為突出的兩大應用性問題。 本文探討了隱現于列聯表分析中辛普森悖論問題,分析了回歸分析中logit變換與probit變換的內在差異與相關假定。認為,辛普森悖論誠然可以通過全概公式加以解釋,但實質上是歐氏空間的降維問題,是列聯表不同維度數據結構的統計信息差異性反映;無論logit與probit函數只有在0.2~0.8之間才基本呈現線性,在這個范圍之外,兩個函數都是高度非線性的。上述兩個應用性問題無疑對于社會統計分析的參數解釋有著特殊的意義。 [1]丹尼爾A鮑威斯(Daniel A.Powers),謝宇.分類數據分析的統計方法[M].北京:社會科學文獻出版社,2009. [2]S.S.Stevens.On the Theory of Scales of Measurement[J].Science. New Series,1946,(103). [3]Glifford,H W.Simpson’s Paradox in Real Life[J].The American Statistician,1982,(36). [4]史希來.屬性數據分析引論[M].北京:北京大學出版社,2006. [5]Thurstone,L.L.A Law of Comparative Judgment[J].Psychological Review,1927,(34). [6]Cox,D.R.The Analysis of Binary Data[M].London:Chapman and Hall, 1970.Finey,D.J.Probit Analysis(3rdEdition)[M].Cambridge:Cambridge University Press. [7]Amemiya,T.Qualitative Response Models:A Survey[J].Journal of Economic Literature,1991,(19). [8]Maddala,G.S.Limited-Dependent and Qualitative Variables in Economics[M].Cambridge:Cambridge University Press. (責任編輯/亦民) C81 A 1002-6487(2011)06-0024-02 教育部人文社會科學研究青年基金資助項目(10YJC840014);中國博士后科學基金資助項目(20100470620) 程中興(1975-),男,安徽懷寧人,博士后,副教授,研究方向:社會研究方法。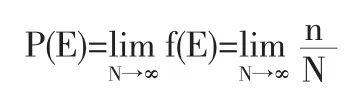
2 變換問題
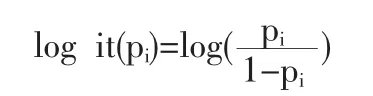
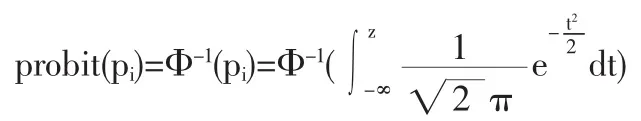
3 結語