金融區間數據的動態回歸模型比較與實證檢驗

王泰積，劉威儀，李竹渝

(1.四川大學數學學院，成都610064；2.北京大學光華管理學院，北京100871)

金融區間數據的動態回歸模型比較與實證檢驗

王泰積1，劉威儀2，李竹渝1

(1.四川大學數學學院，成都610064；2.北京大學光華管理學院，北京100871)

傳統金融時間序列中，對于股價研究多以當日收盤價為基礎。這樣不可避免地會產生觀測信息的損失，從而導致模型解釋能力的降低。文章討論了模糊自回歸（FAR(p)）模型和模糊雙線性回歸（FDLR（p，q））模型結構，并在金融動態數據不同趨勢條件下，直接討論針對區間序列的金融時間序列模型的變化；基于不同特點的金融區間波段，對這兩個模型作了比較研究，進一步討論了模型的擬合評價與解釋能力。

金融區間數據；回歸模型

0 引言

不確定性研究可以分為兩類，一類是隨機的，一類是模糊的。傳統時間序列分析中對股票收盤價的單序列研究，都是基于前者。這些研究從概率性角度出發，借助隨機波動理論模型，完成對金融市場有效數據的解讀。顯然，僅依賴“收盤價”這樣的數據列信息是不完全的，因為股票市場上的金融資產的價格波動給出的信息是以[最低價，最高價]這樣的區間數據列顯示的。盡管收盤價對次日的預測有非常重要的作用，但無須質疑的是，對整體市場波動的考量是有“信息流失”的。筆者提出另一種思路，即直接從金融區間數據出發，構建區間時間序列模型。理論上，就是要從模糊性的角度來解釋不確定性問題。

從數據本身特點而言，區間數據較收盤價序列包含更多的信息。其完整反應出了當前時刻數據既有的波動范圍。比較傳統收盤價單序列結構，區間數據對于波動的描述引入了新的信息，跳出以精確觀測值研究不確定性問題的經典數據模式，具有很大的研究潛力。從數據分析而言，區間數據的模糊刻畫建模，完善了不確定性分析的內涵。這類模型在不確定波動研究中加入非隨機波動的內容，是描述問題的又一個開端。

本文把重點放在模型時序研究上。沒有隨機性假設的模型在運用于實證區間數據分析時，是否依然形成有效解釋是我們將集中討論的問題。其中包括模型對于數據的敏感性，以及模型對數據特點總結的優劣評價。

1 金融區間序列的模糊刻畫

其中(xt,yt)是指以xt為中心、yt為廣度的對稱三角模糊數，稱這樣的序列為區間金融時間序列。

多數的金融研究是針對資產收益率而不是資產價格，Campbell.Lo和MacKinlay（1997）[3]中給出了使用收益率的兩個主要理由：第一，對普通的投資者來說，資產收益率是投資機會的完全的、尺度自由的概括；第二，收益率序列比價格序列更容易處理，因為前者有更好的統計性質。參照傳統金融收益率定義，可以給出如下定義。

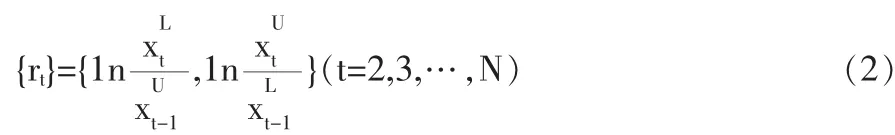
為區間金融收益率序列。

{rt}也可表成對稱三角模糊序列的形式{rt}={(ct,ut),t=2,3,…，N}，其中心序列（反映了金融資產收益率的集中變化趨勢）與廣度序列（反映金融資產收益率非隨機波動性的大小）分別為：

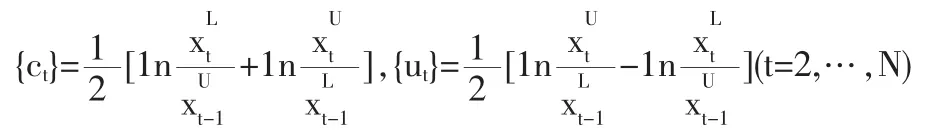
對比傳統收盤價序列收益、波動率分析中所使用的均值—方差結構，這里定義的對稱三角模糊數結構（中心序列與廣度序列）可以理解為一種新的雙序列結構，即中心—廣度序列結構。這是研究金融市場動態風險管理的一種新思路。

定義3 設{rt}={(ct,ut)},t=2,3,…，N}為一區間金融收益率序列，當其中心序列{ct}平穩時，稱區間金融收益率序列{rt}= {(ct,ut)},t=2,3,…，N}條件平穩。

2 金融區間數據的動態回歸模型

這里介紹的兩類模型。基于定義2，由文獻[1]引入模糊自回歸模型（FAR(p)）。

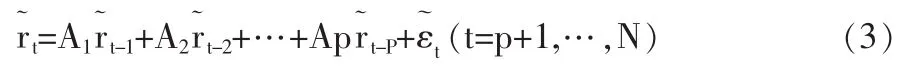
其中，A1，A2，…，Ap∈R為自回歸系數，ε軌t為t時刻的模糊誤差項。

模型（3）描述了區間金融收益率序列在t時刻取值與其滯后p階值的自回歸關系，與傳統時間序列分析的AR(p)模型相似，故稱其為p階模糊自回歸模型，簡記FAR(p)。為了估計FAR(p)模型中的未知回歸系數，可利用模糊線性規劃（Fuzzy Linear Program FLP）方法。FLP方法的基本思想是在滿足所有擬合值和觀測值的貼近度（貼近度的概念可參見陳水利等[4]）達到給定門限值的約束條件下，通過模型回歸系數的選取，使得回歸模型的模糊性指標達到最小，從而將模型（3）回歸系數的估計過程化為一個線性規劃問題的求解過程。模型（3）中未知自回歸參數的估計A軒1，A軒2，…，A軒p可來自如下線性規劃模型的優化求解：

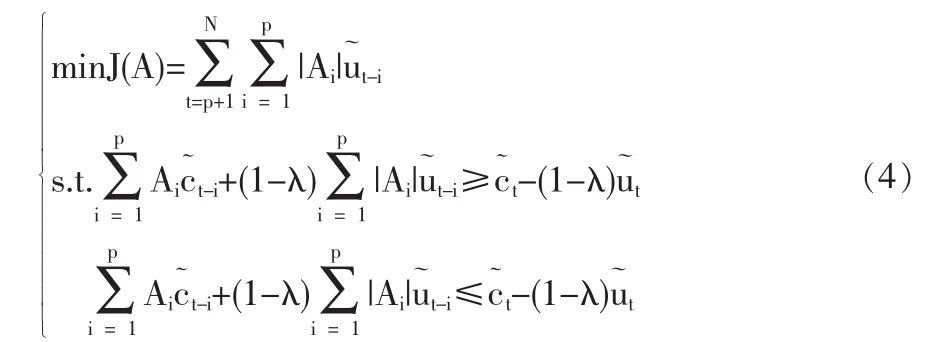
其中，t=p+1，…，N；λ稱為貼近度門限值，可在[0,1]中取值。模糊性指標為該指標與序列的廣度序列緊密相關[1]。廣度序列在描述金融區間序列動態變化時，完全類似于傳統收益率均值-方差分析中方差的作用。廣度序列刻畫了區間金融序列的動態波動情況。因此廣度序列有一個自然的性質：正定性。同時每期觀察點廣度必須為正的要求，就形成該線性規劃求解的模糊性指標中的主要條件限制。

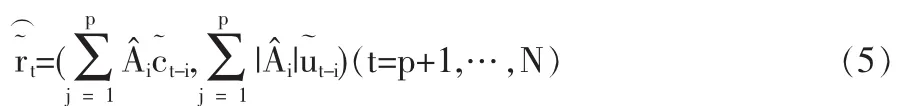
仔細觀察FAR（p）模型（3）、（5），區間序列簡單的整體建模導致區間金融收益率的中心和廣度有相同的變化趨勢，這是FAR(p)模型最明顯的不足。同時，對于并未中心化的數據，收益率模型中的常數項（漂移項）在金融收益率序列建模中不能被輕易省略。在利用（4）解決未知參數估計的過程中，由于其原理是分析線性規劃方程最優解的存在問題，其解的存在性也就與規劃方程的條件密切相關。觀察模糊性指標，可以清楚地看到：這里要求每時刻廣度嚴格為正。隨著觀察區間的增加，邊界條件維數大量增長，使得方程有解的限制增強，參數無解的可能性增加，模型對數據的解釋能力也由此將極大降低。但由于模糊自回歸模型是目前文獻中討論較多的模型，我們將保留此模型對區間數據的分析。

針對FAR（p）模型自身所存在的問題，以及考慮到中心與廣度序列存在一定相依性關系，這里借鑒Pierpaolo D’Urso[5]等（2000）中提出的廣度在動態變化過程中一定程度上依賴于中心的思想，構建了模糊雙線性模型FDLR（p,q）[2]。

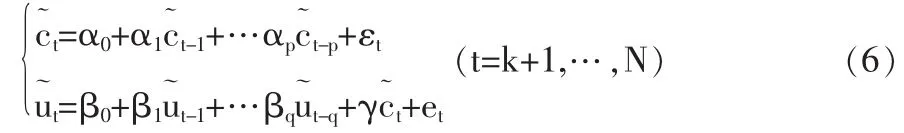
這里k=max(p,q)，且α0,α1，…，αp,β0,β1,…，βq，γ為未知回歸系數，εt和et分別為t時刻中心序列和廣度序列的誤差項。由于涉及中心序列與廣度序列的雙線性與滯后階數的變化，我們命名為（p，q）階的模糊雙線性回歸模型，簡記FDLR（p,q）。

式（6）是建立在兩個線性模型基礎上的：第一個模型解釋了區間金融收益率序列在t時刻收益率的集中趨勢（中心）與其滯后p階值的自回歸關系；第二個模型建立在第一個模型的基礎之上，解釋了區間金融收益率序列在t時刻收益率的波動變化趨勢（廣度）與其滯后q階、以及變化與集中程度的相依關系，解釋了區間金融收益率序列的波動趨勢。

對于模型（6）中未知參數的估計，采用普通最小二乘法，詳細論述可參見文獻[2]。

3 實證分析

3.1 數據選擇與檢驗

金融時間序列分析中，不同的金融波段會導致不同的模型解釋，而上升與下降的收益率波動變化也將是不對稱的。所以，在考慮模型對金融區間數據的解釋能力時，需要選取不同時段的數據，充分考慮波動的變化。我們觀察上證日指數中兩個不同特點的金融區間時段。圖1（a）：2006.11.21～ 2007.10.19，整體呈現上升（220個數據組）。圖1（b）：2008.1.22 ～2009.3.20，整體呈現下降趨勢（共281個數據組）。

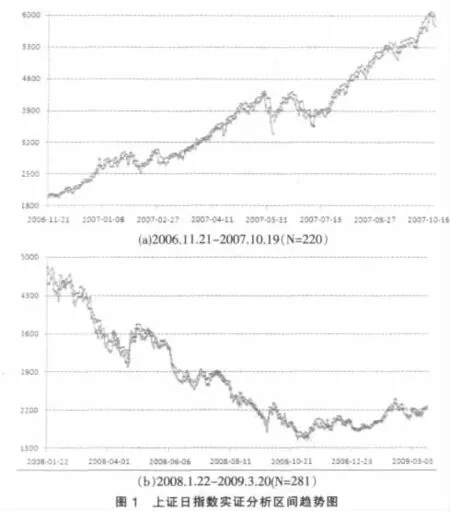
圖2給出了這兩段區間數據的區間收益率中心序列圖示。

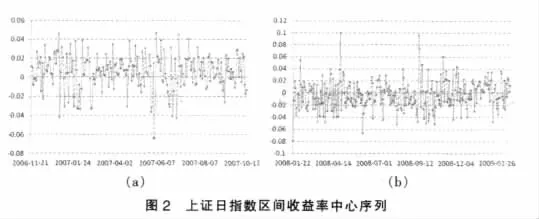
從圖2可見，中心序列集中在0值附近波動。其中上升段更集中于正值，下降段更集中于負值。區間收益率中心序列對于數據信息量的概括，依然能明顯顯現。

平穩性是時序模型的解釋基礎，不論是隨機還是非隨機，數據的平穩是不確定波動收斂的理論基礎。定義3以區間中心為標準所定義的條件平穩雖然并不是廣泛意義下的區間平穩，但如同收盤價收益率序列在傳統分析中的概括作用一樣，它是包含大量區間信息意義下的條件平穩序列。由此，根據定義3中的條件平穩定義，下面給出（a）、（b）序列平穩性的討論。由于這里探討的是非隨機波動性，并未作任何關于分布的假設，借用無先驗分布假設的游程檢驗，其檢驗結果見表1。

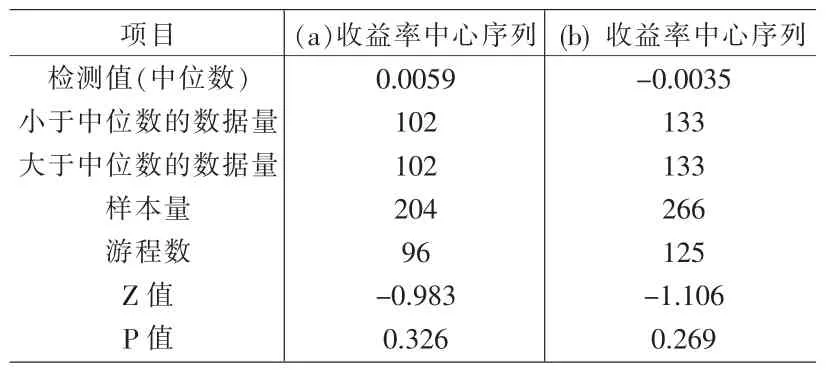
表1 區間收益率中心序列平穩性檢驗

表1中分析結果表明，以中位數為標準的游程檢驗（P值分別為0.326和0.269，大于10%的顯著水平）不能拒絕這兩段數據的條件平穩性，即這里使用的上升和下降區間段都是條件平穩的。

整體上觀察：（a）、(b)段區間數據分別有上升和下降的趨勢，其間的小范圍波動也在各自結構范圍之內，并不影響其整體趨勢。在樣本期內外數據的選取上，盡量使用整周數據，從而不擾亂日數據本身所具有的周效應，以求得盡量合理的分析。下面，利用模型（3）、模型（6）分別對（a）、（b）序列進行實證分析，將取最后三周共15組數據作為樣本期外的模型檢驗樣本。模型擬合評價，采取經典的二階MSE，和一階MAE進行比較。同時，模型對數據解釋的合理性，也是我們探討的重點。

3.2 FAR（1）與FDLR（1,1）實證比較

由于區間模型的定階問題比較復雜，需要考慮到區間數據本身的多重性質，這里不作討論。實證中，根據文獻[6]中提到的金融收益率時間序列的短期強相關經驗，取p=1、q=1進行比較分析。

上升區間（a）段模型擬合結果如下式：FAR（1）模型：

FDLR（1，1）模型：

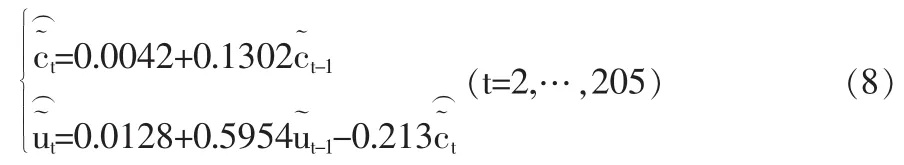
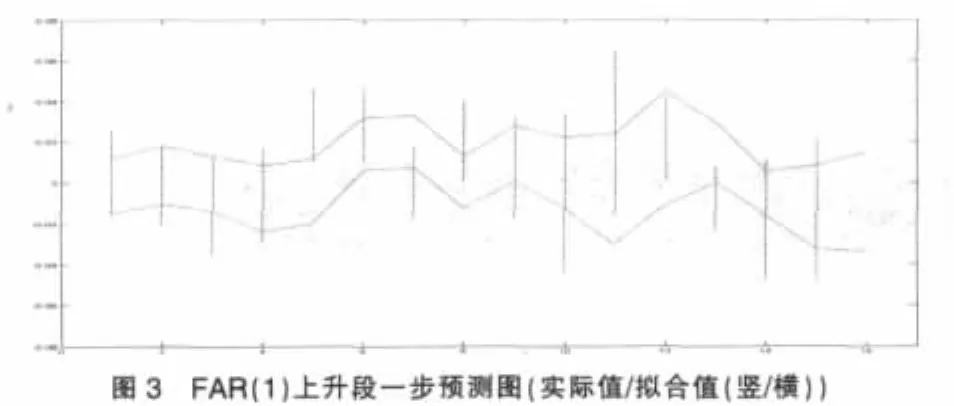
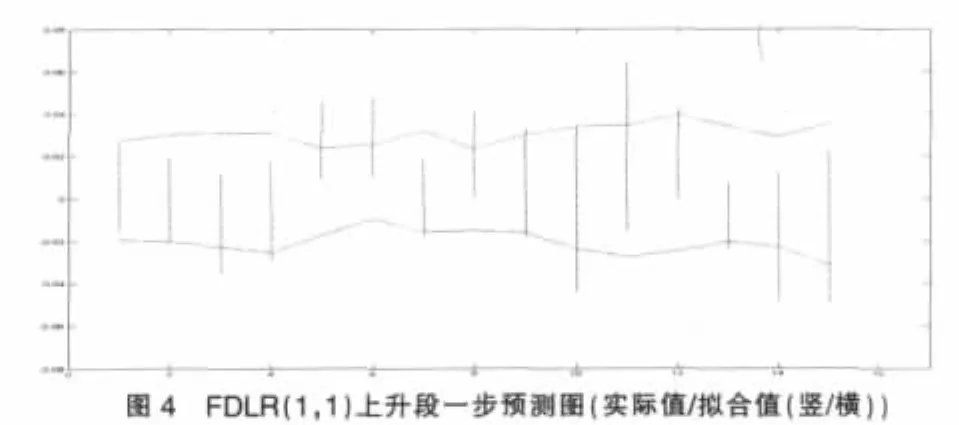
上升區間（a）段模型樣本期外一步預測結果如圖3、4。

下降區間（b）段模型擬合結果如下式：

FAR（1）模型：

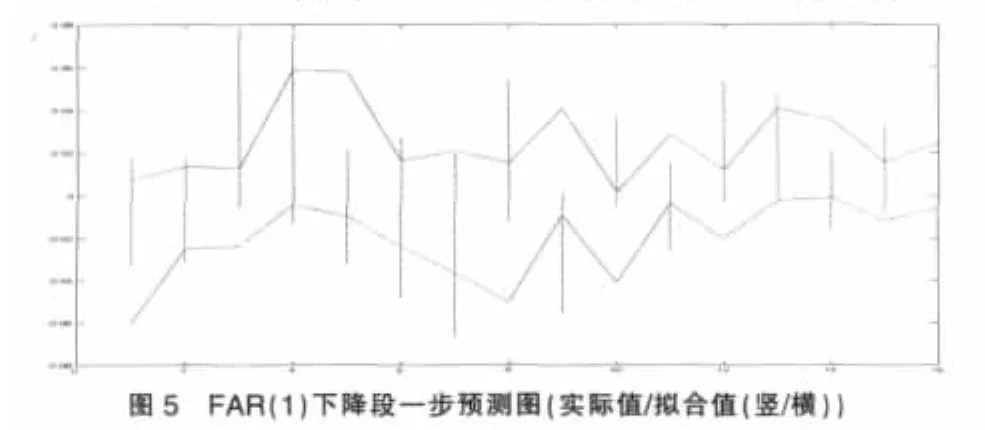
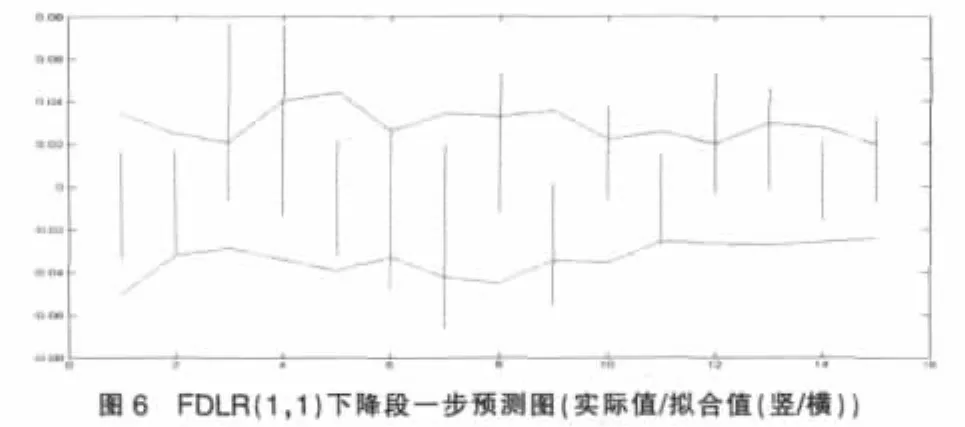
下降區間（b）段模型樣本期外一步預測結果如圖5、6。

圖3～6可直接觀察到模型對于樣本期外預測的一些效果。兩個不同變化時段中，模型對于波動較大的數據，一步預測結果都會出現較大的偏差,FAR(1)模型甚至出現了預測與實際完全偏離的狀況。直觀比較而言，FDLR（1，1）模型的預測效果更趨向平穩。同時FAR（1）模型對于數據的波動反應出較為敏感的狀況，這種敏感甚至帶來走勢的錯誤預測。從圖上粗略的觀察，FDLR表現出更為穩健的效果。

再從擬合模型結果(7)～(10)分析:FAR（1）模型中區間收益率序列的中心與廣度序列是同變的，并且缺少描述數據集中趨勢的漂移項，因此該模型在對于區間序列的解釋能力上，存在一些明顯的不足，并不足以充分描述數據的動態變化。而FDLR（1，1）模型在這些方面做出了很大的改進。從(8)和(10)兩式中，我們可以得到該模型對數據的一些合理描述。

對于上升段區間數據，實證模型（8）表現出：①中心序列漂移項為正（這點與圖形直觀相符），中心序列的滯后一階對其本身的影響是正向的；②廣度序列漂移項為正，波動較為明顯；③廣度序列滯后一階對其當前的影響是正向的，而當前時刻收益序列的集中程度（中心）對其影響為負向，集中程度的強弱變化對區間波動有較大影響。

同樣，實證模型（10）也給出區間數據下降段的一些描述：①中心序列漂移項為負（這點符合圖形直觀），中心序列的滯后一階對其本身的影響是正向的；②廣度序列漂移項為正，波動較為明顯，但較上升段無明顯變化；③廣度序列滯后一階對其本身的影響是正向的，而當前時刻收益序列的集中程度（中心）對其影響為負向，集中程度的強弱變化對區間波動影響遠不及上升段區間數據，顯示出上升、下降區間數據波動變化的不對稱性。

兩個不同金融波段得到的模型總結中，后兩項一致，而中心序列漂移項的改變反映出股市數據結構性變化。于是比較而言，兩段數據的實證分析表明，FDLR（1，1）的實證解釋能力更為全面。

直觀上的模型擬合圖形比較是不嚴格的，利用實際值和擬合值間的距離描述來評價擬合效果，是經典模型評價中最直接有效的方法。這里我們借用兩種不同距離來考察區間模型對于數據的擬合預測效果。

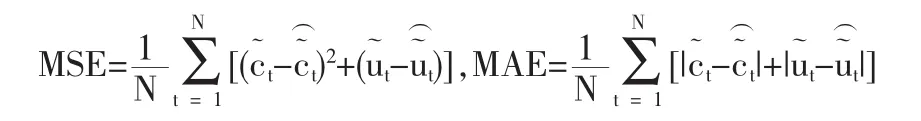
表2給出了利用定義6中MSE、MAE考察不同區間、不同模型對于實際數據的擬合結果。

表2中的結果表明：①對于兩個不同的區間時段：兩個模型都具有一定時變性。即不同的數據結構導致不同的擬合效果。②兩個模型作比較：兩個金融波段中，FDLR（1，1）模型不論是樣本期外還是樣本期內都具有更好的擬合預測效果。

FDLR（1，1）模型中，對上升下降兩個不同特點的金融波段,中心序列對于波動的影響表現出明顯的不對稱。中心序列對于區間波動產生負向影響，即中心有限制波動的作用。但再比較上升下降兩個波段上中心(集中程度)變化對區間波動影響，上升段區間數據遠較下降段數據明顯。區間中心在不同趨勢區間序列中表現出不對稱的影響效應，模型在實證中表現出較強的數據敏感性，這種結構特征是值得進一步仔細研究的。

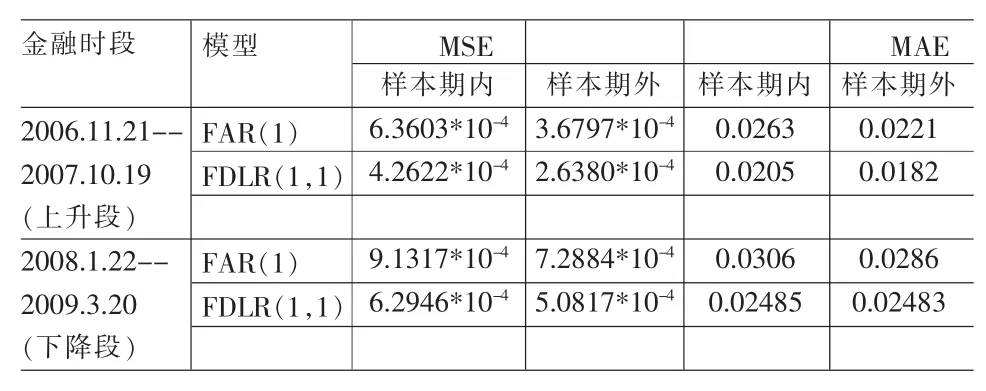
表2 上升區間段與下降區間段模型擬合預測效果評價（MSE/MAE）

4 小結

實證分析表明：對于結構特征單一的區間數據，FDLR（1，1）模型在擬合預測精度上優于FAR（1）模型，其解釋能力更為全面，能反映出區間數據的部分結構特征。對于不同趨勢的條件平穩區間波段，FDLR模型表現出了不對稱的影響效應。這種敏感性的變化能反映模型實證解釋能力，這點也是它有別于FAR模型的特點。

對于FDLR（p，q）模型，模型結構的改進將導致敏感性和解釋能力的改變，如何解決模型穩定性和數據敏感性之間的關系也將是我們下一步討論的重點。同時，僅對模型做實證分析，僅僅是模型對實際應用的一種探討，對模型的合理性和有效性還需要做模型仿真模擬的實驗研究，這是我們對金融區間數據建模研究的重點，也是與模型定階問題有關的問題。

全球金融危機后引發的一個突出問題就是：人們開始相信傳統研究所依賴的“風險預報，也會出錯”，“傳統模型失誤系數有可能非常高”。這就是說：實際風險與預測風險之間可能存在顯著差異。探索新的視角、新的研究思路、運用交叉學科知識構建綜合研究平臺以利開發新的、更完善、信息損失更少、能更好地處理市場波動不確定性的模型，來研究風險管理問題已經是大勢所趨。

從模型角度來看，直接對以中心—廣度為基本結構的區間數據建模分析，是研究市場波動的新思路。結合區間數據自有的模糊性探討不確定現象，特別是在缺少隨機性假設的條件下，這是對市場波動另一個角度的研究。從不確定中挖掘確定，從雜亂波動中提取規律是人們長期關注的話題。在有限認知能力下，多角度研究不確定性將為這一探索帶來新的發現。

[1]李竹渝，張成，王泰積.金融區間序列分析及其預測的初步評價[J].數理統計與管理，2010，29（1）.

[2]Wang Taiji,Liu Weiyi,LI Zhuyu.Fuzzy Double Linear Regression of the Financial Assets Yield[Z].Cutting-Edge Research Topics on Multiple Criteria Decision Making(MCDM2009):Springer-Verlag,2009.

[3]Campbell,Lo,MacKinlay（1997）The Econometrics of Financial Markets[M].朱平芳，劉弘譯.上海：上海財經大學出版社，2003.

[4]陳水利，李敬功，王向公.模糊集理論及其應用[M].北京：科學出版社,2005.

[5]Pierpaolo D’Urso,Tommaso Gastaldi.A Least-Squares Approach to Fuzzy Linear Regression[J].Computational Statistics&Data Analysis,2000，10.

[6]Ruey S.Tsay.金融時間序列分析（第一版）[M].潘家柱譯.北京：機械工業出版社，2006.

（責任編輯/亦民）

C812

A

1002－6487（2011）06－0028-04

國家社會科學基金資助項目（07BTJ003）