變環境條件下型號設備的可靠性估計
胡堯,盧大遠
(貴州大學數學系,貴陽550025)
變環境條件下型號設備的可靠性估計
胡堯,盧大遠
(貴州大學數學系,貴陽550025)
文章討論了變環境條件下,Weibull壽命分布型號設備可靠性的估計問題:固定形狀參數,在壽命特征參數為環境指標一元多項式情形下給出了可靠性估計方法;利用強大數律及控制收斂定理證明了估計量的強相合性,并通過大量仿真數據模擬說明了方法的可用性。
變環境;Weibull分布;可靠性估計;強相合性
0 引言
變環境條件下同型號設備的可靠性會發生變化。隨著環境指標的不斷惡化或不斷改善,可靠性形成環境指標的函數,稱為可靠性曲線[1][2]。估計出該條曲線后,就可以對變環境情形下的型號設備可靠性給出合理的預測。文獻[1]針對Lognoraml類壽命分布,在完全樣本情形下研究了同型號設備不同環境下的可靠性估計問題,文獻[2]在完全樣本情形下,對Lognormal與Weibull兩類壽命分布變環境可靠性估計問題作了進一步的研究,得出可靠性與環境指標的單調遞增關系。本文擬在文獻[1][2]的基礎上,針對Weibull類型號設備壽命分布情形,研究壽命特征參數η與環境指標的關系,給出Weibull類變環境完全樣本條件下的可靠性估計問題,并證明相關研究理論,通過模擬說明估計方法的可用性。
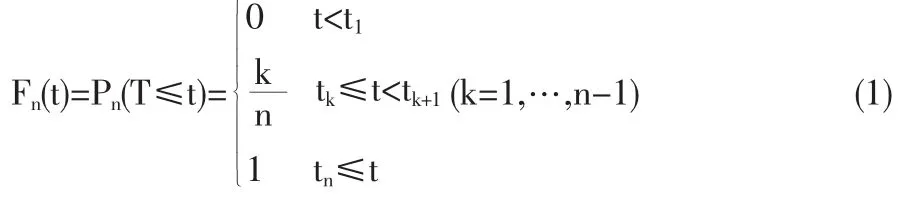
用T表示某型號設備在正常使用環境下的壽命時間,稱該型號設備至少能正常工作t單位時間的概率R(t)=P(T>t)為型號設備的可靠性。可靠性估計是產品質量評估中的常見問題,如果給定i.i.d.序列T1,T2,…,Tn,定義隨機事件,用經驗分布函數估計F(t),從而可用Rn(t)=1-Fn(t)估計型號設備的可靠性R (T)。由Glivenko-Cantelli定理可知Fn(t)幾乎必然(a.s.almost surely)收斂于F(t),理論上可以證明Rn(t)也a.s.收斂于R(t),即Rn(t)是R(t)的強相合估計,故用Rn(t)作為R(t)的估計。當n→∞時,由中心極限定理CLT(central limit theorem)可得
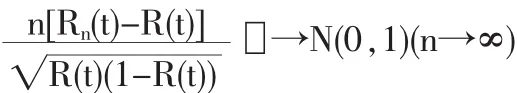

其中
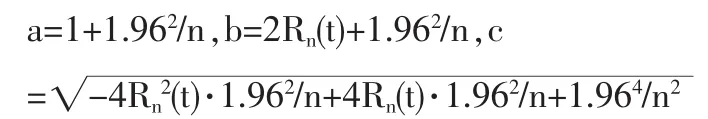
同理,可以構造出R(t)的置信度為1-0.05的近似置信上、下限分別為
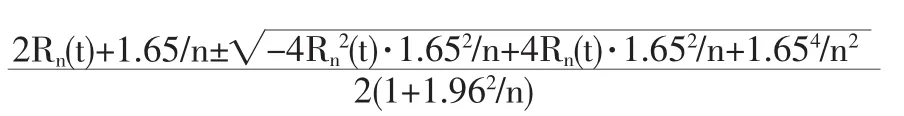
在具體工程問題中,型號設備的可靠性隨著使用環境的惡化或改善其環境指標e也隨之變化,環境指標e可以是單一指標如溫度、濕度、震動、電流、電壓等,也可以是用級別表示的變環境指標的綜合。用Te表示在變環境指標e下型號設備的使用壽命,Re(t)表示變環境指標e條件下型號設備的可靠性。給定總體Te的簡單隨機樣本
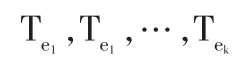
由前所述可用R贊e(t)估計Re(t),對于每個變環境指標e1 在型號設備的可靠性研究中,Weibull分布[4]是一種很有用的壽命分布,已普遍運用于各類壽命設備可靠性評估分析中。本文從應用的角度出發,假定變環境指標為e時,型號設備壽命總體Te服從Weibull分布,則型號設備的可靠性[5]為 由于Weibull分布的形狀參數β,僅表明失效模式或失效機理的類型,與型號設備的使用環境關系不大,變化甚微。在此假定為常數或恒量(β≥1),即各類環境指標下其型號設備失效機理相同,而壽命特征參數η與環境的變化有緊密聯系,假定其與環境指標e的函數關系為η(e),本文假定關系為 如果η(e)在[a,b]內單調增加(或減少),本文證明了可靠性Re(t)在[a,b]內單調增加(或降低),并稱此時的η(e)為(0,e)內的環境改善(或惡化)模型。 給定不同變環境指標下的樣本 其中e(i)為ei的順序統計量。 下面將給出Re(t)的一致強相合估計和預測,并利用計算機隨機模擬驗證估計量和預測估計量的實用性。 定理1設Te服從Weibull分布,其可靠性由(3)式定義 (1)若η(e)在[a,b]內單調減少,則η(e)為[a,b]內的環境惡化模型; (2)若η(e) 在[a,b]內單調增加,則η(e)為[a,b]內的環境改善模型。 證明:對于e∈[a,b],設Te服從于Weibull(β,η(e))(β≥ 1),則對當η(e)單調減少時 故Te隨機小于Ts,根據可靠性定義,于是得到Re(t) 在實際問題中,由于形狀參數β如前所述,隨環境指標e變化緩慢,只有壽命特征η(e)隨e變化,即有關系η(e),故本文假定在較短的時間段內將β視為微小變化,隨后的模擬計算視為常數(通常是(β≥1)且不隨環境指標變化)。 給定環境指標(5)式,對于每個固定的i,Te(i)j(j=1,2,…,ni)是來自分布總體Weibull(βi,ηi),其中βi的極大似然ML(maximum likelihood)估計值滿足 ηi-η(ei)的可由(7)式計算得 這樣就可以得到 即 記 則有(10)式可寫成 當rank(E)=p+1≤k時,E的前p+1行構成Vandermonde行列式。故E是可逆矩陣,即可從(4)式得到 其中ET為E的轉置,依據多元線性回歸模型理論[7]可得回歸系數b=(b0,b1,…,bp)T的最小二乘估計LSE(least square estimate) 定理2設rank(E)=p+1≤k有環境指標數據e(1),e(2),…,e(k),總體Ti=Te(i)的可靠性Re(i)由(3)式定義,假設不同的總體Ti是相互獨立的,對于來自總體Ti的樣本Tij(i=1,2,…,k;j=1,2,…,ni),則有 利用(8)式和內積不等式可得 表1樣本為500個重復2000次時的可靠性估計 即結論(2)成立。下面討論預測問題。 對于a 定義β的估計量 用 作為可靠性Re(t)的估計。 證明:由定理2得 其中c0是只與a,b,k,p有關的常數,由強大數律SLLN (strong laws of large numbers)可證分別是σ2、η、β的強相合估計,用控制收斂定理即有R贊e(t)幾乎必然a.s.收斂于Re(t),又與Ret(a≤e≤b)單調連續,故在區間a≤e≤b上一致收斂于Re(t)。 2.1,2 .3,2.5,2.7,2.8,2.9,3.1,3.2,3.4,3.5,3.6,3.7,3.9,4.1,4.2,4.5 用MATLAB分別產生500個參數為(η(ei),β)的Weibull隨機變量,利用(6)、(7)式計算參數ηi與βi的極大似然估計MLE值,利用(13)式與(15)式計算ai的最小二乘估計LSE值,再利用(14)式計算與β,最后利用(16)式計算出可靠性估計值 通常考慮各種隨機因素的影響,將上述步驟獨立重復2000次,用mean(R贊e(t))表示這2000次計算結果的樣本均值,用表示這2000次計算結果的樣本方差表示各類環境指標下的真值,結果比較下表1。 圖1是模擬分析一真值η(e)與重復2000次的估計值η贊(e)。 案例2 用同樣的方法,取β=2,每次隨機產生1000個隨機數據,獨立重復2000次計算結果如表2。 表2 樣本為1000個重復2000次時的可靠性估計 圖2是模擬分析二真值η(e)與重復2000次的估計值η贊(e)。 模擬計算結果顯示,前面所提出的變環境可靠性計算方法其精度通常能達到實際Weibull型號設備的可靠性評估要求。本文提出的變環境模型基本解決了不同運行環境指標下的Weibull類產品的可靠性預測問題;同時為變環境情形下變參數變動統計學可靠性問題應用研究打下了一定的理論基礎,為進一步研究不完全樣本(刪失、截尾、分組數據)或無失效壽終數據的可靠性估計或評估問題帶來一定的契機。 [1]何書元,趙宇,房祥忠.估計不同環境下的設備可靠性[J].數理統計與管理,2007,26(6). [2]Yao Hu,Mei Yang.Equipment Reliability Estimation of Complete Samples Under Varied Environment[J].ICRMS,2009(7). [3]陳家鼎,孫山澤,李東風.數理統計學講義[M].北京:高等教育出版社, 1993. [4]Dr.Robert B.Abernethy.The New Weibull Handbook(4thEdition) [M].Printings,2003,(8). [5]陳家鼎.生存分析與可靠性[M].北京:北京大學出版社,2005. [6]魏宗舒等.概率論與數理統計教程[M].北京:高等教育出版社,2003,(6). [7]王松桂,陳敏,陳立萍.線性統計模型[M].北京:高等教育出版社, 1999. (責任編輯/亦民) O212 A 1002-6487(2011)06-0032-03 貴州省自然科學基金資助項目(黔科合J字[2008]2048號);貴州省科技計劃資助項目(黔科合SY[2010]3002);貴州大學創新性實驗資助項目(貴大國創字(091065706)號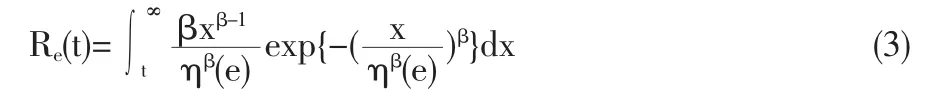


1 主要結果及證明

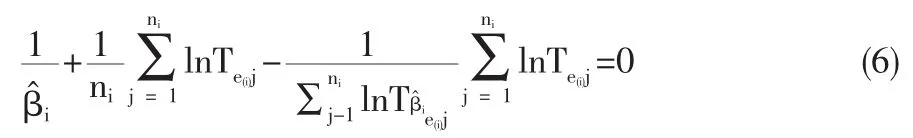

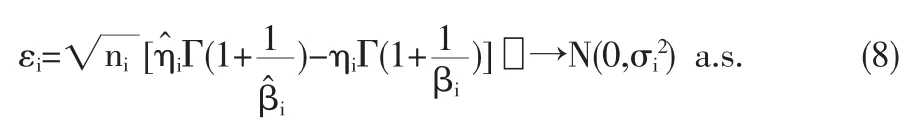

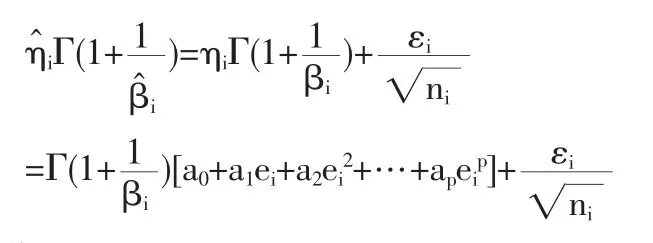
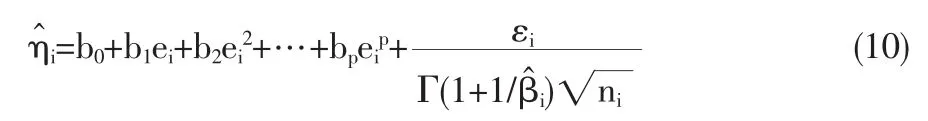



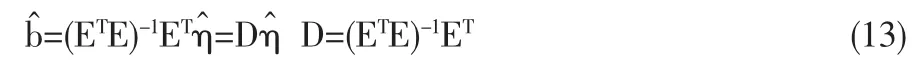

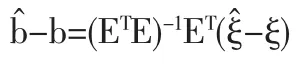
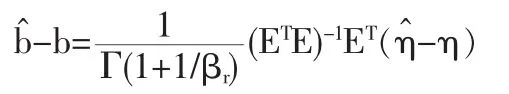
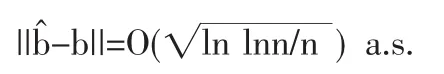

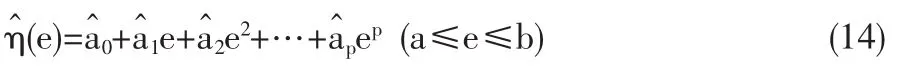

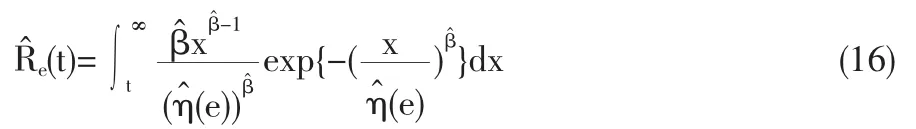
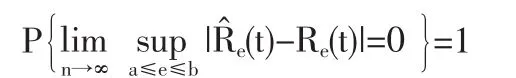
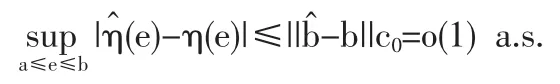
2 模擬計算分析
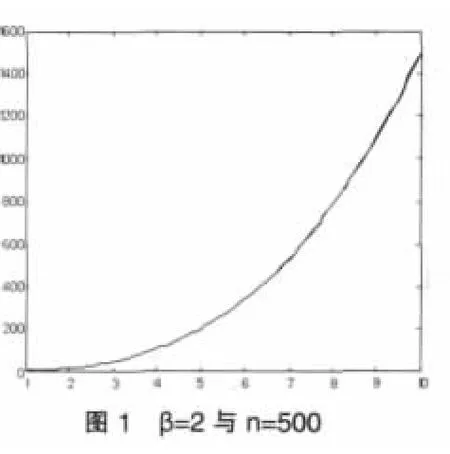
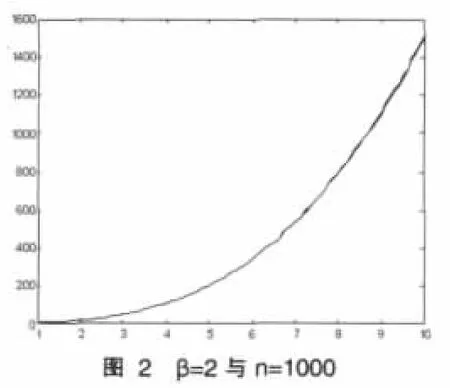

3 結論

