利用動態規劃求解資源分配問題的單表迭代法
宋占嶺 冀秀春 炮兵指揮學院,河北宣化 075100
利用動態規劃求解資源分配問題的單表迭代法
宋占嶺 冀秀春 炮兵指揮學院,河北宣化 075100
將用動態規劃求解資源分配問題時的各階段迭代表格進行統一集成,利用基本方程遞推關系式在同一表格中進行迭代,層次清晰,結果直觀,利于計算機編程實現。
動態規劃;資源分配問題;迭代法
動態規劃是運籌學的一個重要分支,它是解決多階段決策過程最優化的一種數學方法。這一方法最初是由美國數學家貝爾曼(R. Bellman)等人在20世紀50年代提出的。它根據多階段決策問題的特點,把多階段決策問題變換成為一系列相互關聯的單階段決策問題,然后逐個加以解決。動態規劃的核心是最優性原理,即無論過去的狀態和決策如何,對前面的決策所形成的狀態而言,余下的諸決策必須構成最優策略。動態規劃在工程技術、企業管理、工農業生產及軍事等領域中都有廣泛的應用,并且取得了顯著的效果。實踐證明許多問題用動態規劃求解比用線性規劃或非線性規劃更加有效,特別是對離散性問題,運用解析數學無法解決,而動態規劃就成為得力的工具。
1. 資源分配問題的動態規劃模型
資源分配問題亦稱投資問題,其一般提法如下:
設總投資額為a萬元,擬投資于幾個項目上,已知對第i個項目投資xi萬元,收益函數為gi(xi)。問應如何分配資金才可以使總收益最大?

當gi(xi)為線性函數時,它是一個線性規劃問題;當gi(xi)為非線性函數時,它是一個非線性規劃問題。為了應用動態規劃方法求解這類靜態規劃問題,可以人為地賦予它“時段”的概念,將投資項目排序,假想對各個投資項目有先后順序。首先考慮對項目1的投資,然后考慮對項目2的投資,依次最后考慮第n項投資,這樣就把原問題轉化為n階段的決策過程。把問題中的變量xi作為決策變量,將累計的量或隨遞推過程變化的量設為狀態變量。
狀態變量sk表示第k階段可用于第k個到第n個項目的資金數,顯然有s1=a,sn=0。
決策變量xk即應分配第k個項目上的投資額。
狀態轉移方程 sk+1=sk-xk。
最優指標函數fk(sk) 表示當可投資金數為sk時,投資于剩余的n-k+1個項目的最大收益。則基本方程為
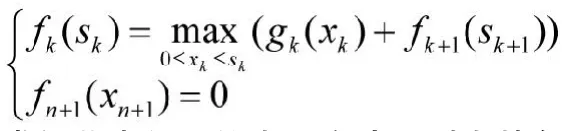
求解此類問題的常用方法是列出其各階段投資決策收益表,利用基本方程遞推關系式進行逐級迭代,最后求得f1(a)即為所求問題的最大收益,我們稱之為“多表迭代法”。下面以文獻[1]213頁例1介紹之。
問題描述:某工業部門根據國家計劃安排,擬將某種高效率的設備五臺,分配給所屬的甲、乙、丙三家工廠,各廠獲得這種設備之后可以為國家提供盈利如表1所示。問這五臺設備如何分配給各廠,才能使國家得到利益最大。
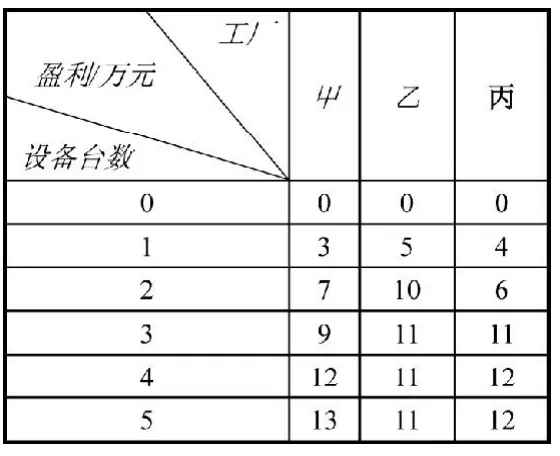
表1
建立模型后,其基本方程為
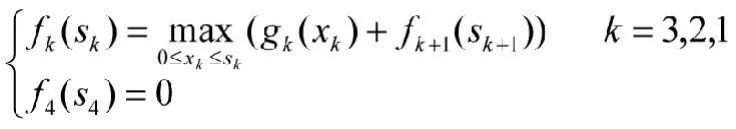
多表迭代求解過程如下:
k=3時,數值計算如表2所示。
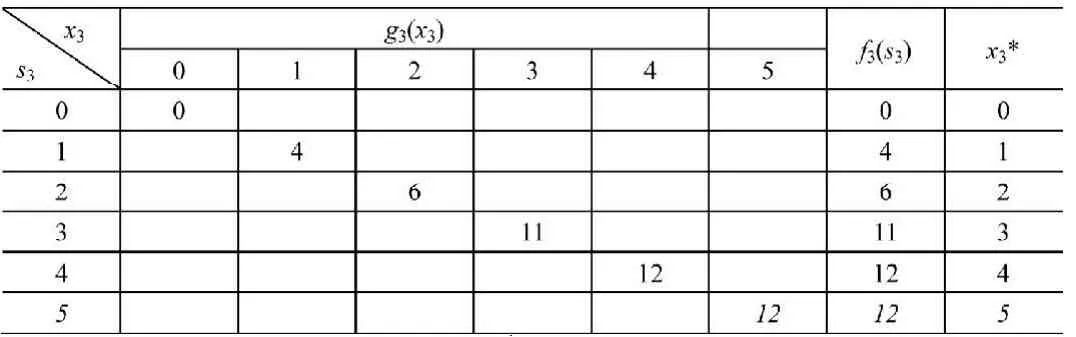
表2
k=2時,數值計算如表3所示。
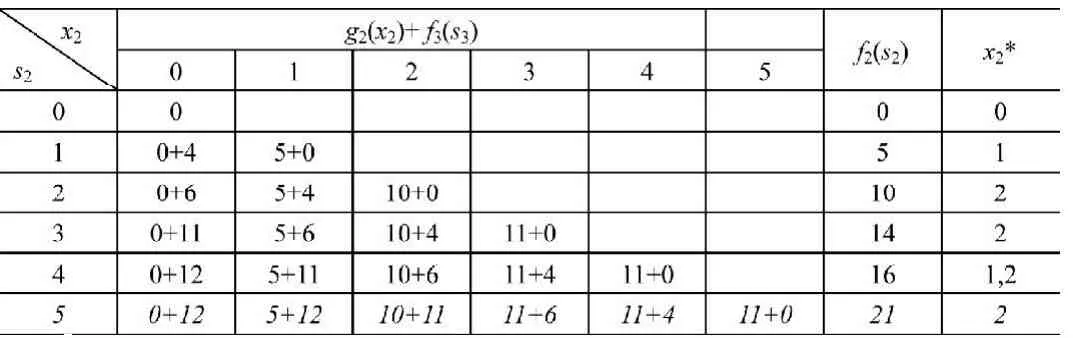
表3
k=1時,數值計算如表4所示。

表4
最后按計算表格順序反推,可知最優分配方案有兩個:甲、乙、丙三廠分別分配0、2、3臺及2、2、1臺,均達到總盈利最大為21萬元。
多表迭代法原理清晰,直觀明了,但模型中有幾個階段就要列出幾個表格,然后利用表格數據進行反復迭代,顯得有些繁瑣,不便于計算機編程實現。為此,筆者將各階段表格進行統一集成,利用基本方程遞推關系式在同一表格中進行迭代,以利于計算機編程實現,稱之為“單表迭代法”。
2. 單表迭代法
單表迭代法計算步驟為:
(1)求出各階段最優指標函數值,存放于迭代表中;
(2)將各階段每一可能狀態條件下的各指標函數與下一階段的最優指標函數交叉相加后尋優,同時標出最優路徑;
(3)根據最優路徑確定最優決策。
前述問題求解結果見表5。
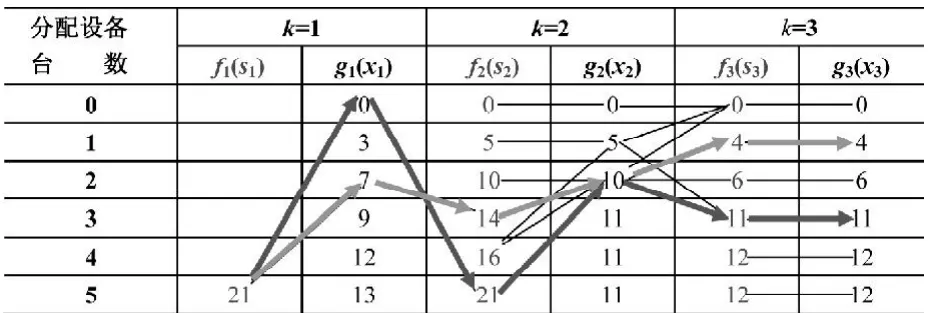
表5
單表迭代法在求解較大規模的問題時,具有很大的優越性。表6中的投資分配問題中,有6個單位的資源和4個方案,各方案在不同投資額條件下收益不同(具體數值參見表6),建立模型后,其基本方程為
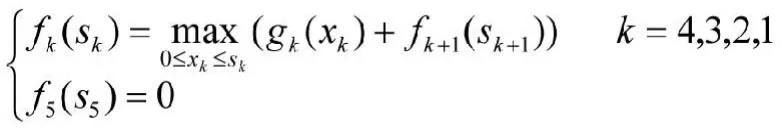
用單表迭代法求解獲益最大的投資結果見表6 。
由表6中迭代結果可知,此投資問題的最大收益為220個單位,共有5個最優方案可實現之。
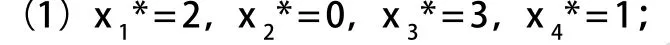
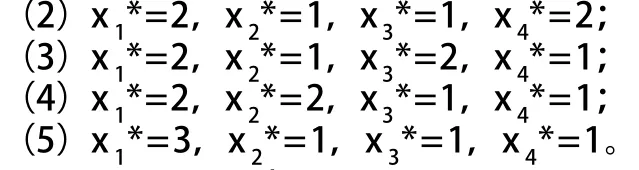
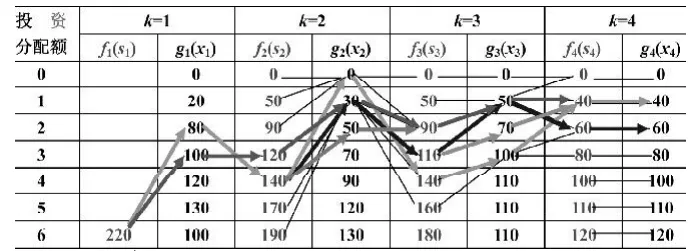
表6
3. 結論
利用動態規劃求解資源分配問題的“單表迭代法”將“多表迭代法”的多個表格統一集成為一個表格,所有迭代計算都在同一表格中進行,層次清晰,結果直觀,更便于計算機編程實現。單表迭代法對于順序遞推基本方程以及最優取最小值的資源分配問題同樣適用。
[1] 運籌學教材編寫組. 運籌學(第三版)[M]. 北京:清華大學出版社.2001
[2] 張野鵬. 軍事運籌基礎[M]. 北京:高等教育出版社.2006
10.3969/j.issn.1001-8972.2011.10.028
作者信息
宋占嶺(1968—),男,河北宣化人,碩士;研究方向:軍事運籌學。

