沒(méi)有任意非零4-流的圖邊數(shù)的新極值

劉彥芬 秦健 楊星星

（1.永城職業(yè)學(xué)院，河南 永城 476600；2.徐州建筑職業(yè)技術(shù)學(xué)院，江蘇 徐州 221116；3.中國(guó)礦業(yè)大學(xué)，江蘇 徐州 221008）

沒(méi)有任意非零4-流的圖邊數(shù)的新極值

劉彥芬1秦健2楊星星3

（1.永城職業(yè)學(xué)院，河南 永城 476600；2.徐州建筑職業(yè)技術(shù)學(xué)院，江蘇 徐州 221116；3.中國(guó)礦業(yè)大學(xué)，江蘇 徐州 221008）

在文獻(xiàn)[7]中Tutte介紹了任意非零流，后來(lái)被廣泛的研究。為了得到較好的界值，論文運(yùn)用圖收縮的方法，給出了圖沒(méi)有任意非零4-流時(shí)邊數(shù)的新極值。上述的極值改進(jìn)了[5]中的結(jié)論。

邊數(shù)；任意非零4-流；2邊連通

0 引言

本文研究的是有限的、無(wú)環(huán)但可能含有平行邊的圖。未定義的術(shù)語(yǔ)和記號(hào)參見(jiàn)文獻(xiàn)[1]，n表示n階循環(huán)群，其中n為某個(gè)n≥ 2的整數(shù)。設(shè)D( G )表示無(wú)向圖G的一個(gè)定向。為了方便，用D表示D( G)。設(shè) EG(v)表示在圖中與v點(diǎn)關(guān)聯(lián)的邊的集合。對(duì)于一點(diǎn)v∈V( D )，

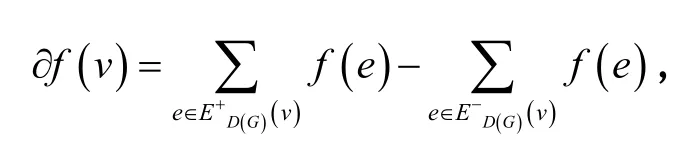
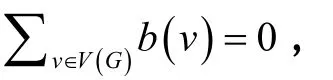
Tutte在文獻(xiàn)[7]中介紹了任意非零流，并且非零流被廣泛的研究，參見(jiàn)文獻(xiàn)[8]。 一個(gè)圖有ANZF?的必要條件是2-邊連通的。對(duì)于整數(shù)k≥2，用 Fk表示有任意非零 Zk-流的全部圖的集合，由定義得

眾所周知，Petersen圖P10沒(méi)有4?NZF，并且當(dāng)n為一奇數(shù)， n+1個(gè)頂點(diǎn)的輪圖Wn沒(méi)有3?NZF。于是自然的就考慮：對(duì)于k∈{3 ,4}，使得2-邊連通的n階簡(jiǎn)單圖至少具有f( n, k)條邊，就有k?NZF的函數(shù)的存在性。本文就是考慮k=4時(shí)，使得2-邊連通的n階簡(jiǎn)單圖至少具有f( n, k)條邊，就有4?NZF的函數(shù)的存在性。

1 主要引理

引理1[4]設(shè)G為階數(shù)為n (n≤17)且2-邊連通的圖，則G∈F4或者G能被收縮到petersen圖。

引理 2[5]設(shè)G′是G的簡(jiǎn)約圖，則G′∈F4當(dāng)且僅當(dāng)G∈F4。

引理 3[6]設(shè)G是2-邊連通的非平凡的簡(jiǎn)約圖，則G為簡(jiǎn)單圖且

引理 4[5]設(shè)G是2-邊連通且階數(shù)為n的簡(jiǎn)單圖，取p為滿足p≥2的整數(shù)，如果

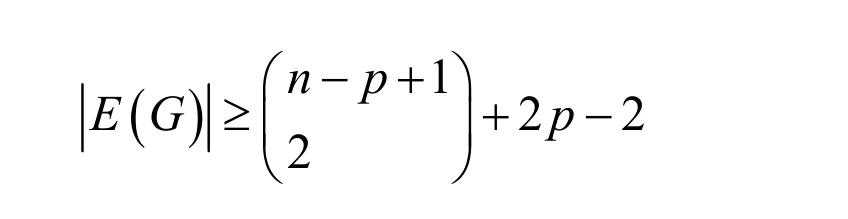
那么G的約簡(jiǎn)至多有p?1個(gè)頂點(diǎn)。

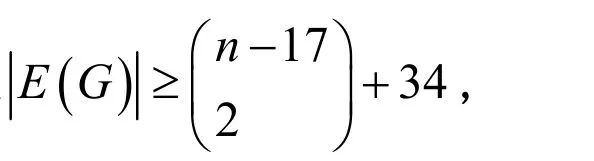
那么G有一個(gè)4-NZF，或者G可以收縮成Petersen圖。

2 主要結(jié)論及證明

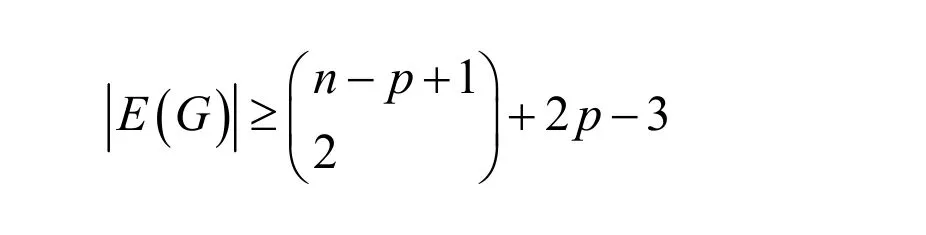
那么，G的約簡(jiǎn)圖至多有p?1個(gè)頂點(diǎn)。

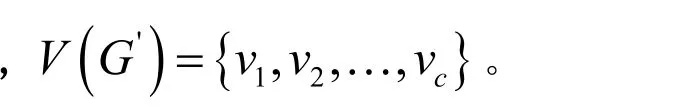
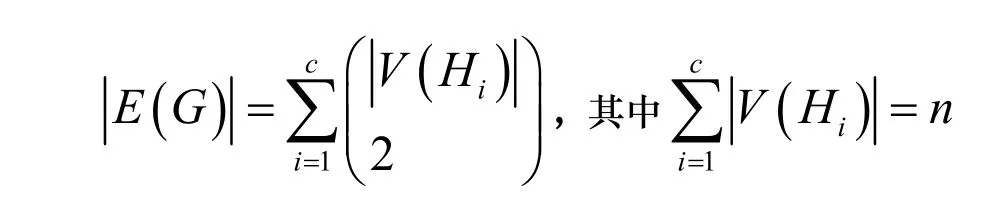
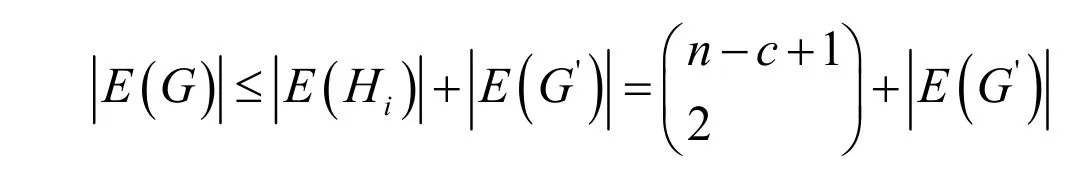
因?yàn)镚為2-邊連通圖，c≥p≥2，G'是非平凡的，由引理3，

于是有，

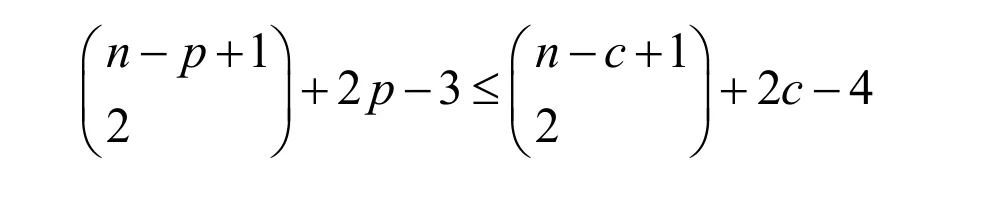
化簡(jiǎn)得

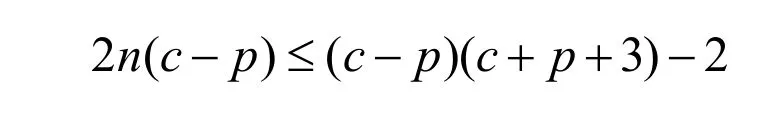
若c=p，上式顯然不成立。故c＞p;。

所以

所以假設(shè)不成立，即c＜p。也就是，c≤p?1。

故G的約簡(jiǎn)至多有 p?1個(gè)頂點(diǎn)。

基于上述的引理2.1，有下面的定理2.2成立。

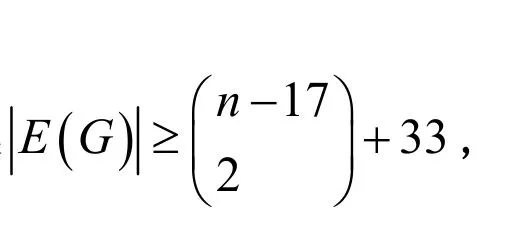
那么G有一個(gè)4-NZF，或者G可以收縮成Petersen圖。

證明：取p=18，由引理2.1，G的約簡(jiǎn) G'至多有17個(gè)頂點(diǎn)。再由引理1可知，G的約簡(jiǎn) G'∈F4，或者G'可以收縮成Petersen圖。

若G'∈F4，由引理3知，G∈F4。

若G'可以收縮成Petersen圖，則G可以收縮成Petersen圖。

所以定理2.2成立。

上述的定理2.2的結(jié)論與文獻(xiàn)[5]中的定理1.3(見(jiàn)上述的引理5)的結(jié)論相同，但條件有了減弱。盡管只是將邊數(shù)減少了1，

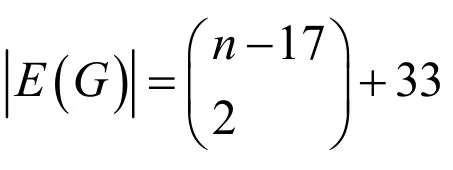
這樣的圖存在無(wú)數(shù)多個(gè)。

[1] J.A.邦迪, U.S.R.默蒂(吳望名,李念祖,吳蘭芳等譯).圖論及其應(yīng)用[M].北京:科學(xué)出版社,1984.

[2]鄭藝容.乘積圖的非零整數(shù)流和完美匹配單圈圖的特征值[M].福州:福州大學(xué)碩士學(xué)位論文,2005.

[3]尚華輝,苗連英,苗正科.沒(méi)有任意非零3-流圖的一個(gè)新下界[J].山西大學(xué)學(xué)報(bào)(自然科學(xué)版) ,2009, (3): 341-344.

[4]J.J.Watkins and R.J.Wilson.A survey of snarks[J].Graph theory, Combinatorics，and Applications, Wiley New York, 1991, 2,1129-1144.

[5]H.J.Lai.,The size of graphs without a nowhere zero 4-flow[J].J.Graph Theory.1995,19, 385-395.

[6]P.A.Catlin,A reduction method to find spanning Eulerian subgraphs[J].J.Graph Theory.1988,12,29– 45.

[7]W.T.Tutte, A contribution to the theory of chromatic polynomials[J].Canad.J.Math, 1954, 6: 80-91.

[8]F.Jaeger, N.Linial, C.Payan, and N.Tarsi, Group connectivity of graphs – a nonhomogeneous analogue of nowhere zero flow properties[J].J.Combinatorial Theory, Ser.B, 1992, 56: 165-182.

[9]F.Jaeger, Flows and generalized coloring theorem in graphs[J].J Combin Theory Ser B, 1979, 26:205-216.

[10]C.Thomassen, Gr¨otzsch’s 3-color theorem and its counterparts for the torus and the projective plane[J].J Combin Theory Ser B,1994, 62:268-279.

[11]C.Thomassen, 5-coloring graphs on the torus[J].J Combin Theory Ser B, 1994, 62: 11-33.

[12]W.T.Tutte, On the imbedding of linear graph into surfaces[J].Proc London Math Soc Ser 2, 1949, 51: 464-483.

[13]P.A.Catlin, The reduction of graph family closed under contraction[J].Discrete Math ,1996, 160: 67-80.

[14]C.Q.Zhang, Integer flows and cycle covers of graphs[M].Marcel Dekker, New York, 1997.

[15]J.J.Chen, E.Eschen, H.J.Lai, Group connectivity of certain graphs[J].Ars Combinatoria, 2008,89:141-158

[16]Y.X.Yao, X.W.Li, H.J.Lai，Degree conditions for group connectivity[J].Discrete Math, 2010,310:1050-1058.

O157.5

A

1673-2219（2011）04-0009-04

2011－01－05

劉彥芬（1981－），女，河南南陽(yáng)人，永城職業(yè)學(xué)院教師，主要從事圖論及其應(yīng)用方面的研究。

（責(zé)任編校：京華）