考慮剪切變形波形鋼腹板組合箱梁抗彎剛度實用計算方法

李世深 孫斌

1 廣西大學土木建筑工程學院，廣西 南寧 530004

2 中鐵二十工程局集團第四工程公司，山東 青島 266061

考慮剪切變形波形鋼腹板組合箱梁抗彎剛度實用計算方法

李世深1孫斌2

1 廣西大學土木建筑工程學院，廣西 南寧 530004

2 中鐵二十工程局集團第四工程公司，山東 青島 266061

本文假設組合箱梁的彎矩M全部由翼板來承擔，剪力Q由波形剛腹板來承擔，按照考慮剪切變形的Timoshen梁ko彎曲理論，推導出考慮波形剛腹板剪切變形的彎曲剛度計算式，在此基礎上，將彎矩M按三角級數展開并近似取第一項，利用三角函數導數性質，得到簡單的考慮波形剛腹板剪切變形對抗彎剛度折減系數表達式。通過驗證模型，驗證了這種等效在集中荷載和均布荷載下具有良好的精度。

波形剛腹板；組合箱梁；抗彎剛度；實用計算方法

引言

波形鋼腹板組合箱梁由兩種不同性質的材料組成，同時，波形鋼腹板具有縱向褶皺效應[3]，其抗彎抗扭剛度計算跟傳統箱梁有區別，而結構剛度在設計計算或者研究分析中會涉及，本文分析波形鋼腹板組合箱梁彈性階段抗彎和抗扭剛度，為彎扭分析作準備。

1 考慮波形鋼腹板剪切變形對截面抗彎剛度的折減系數

圖1是一個波形鋼腹板組合箱梁簡支梁橋及斷面。如圖2，在計算豎向撓度V時，把梁看成這樣的整體梁式受力構件：彎矩M由翼板完全承受，剪力Q由波形鋼腹板承受[1]。

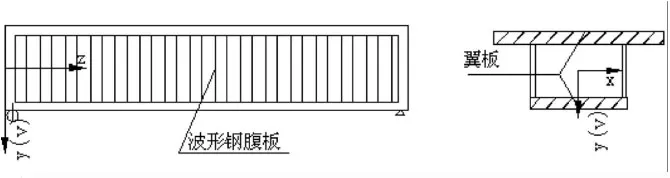
圖1 波形鋼腹板組合箱梁簡支梁橋及斷面

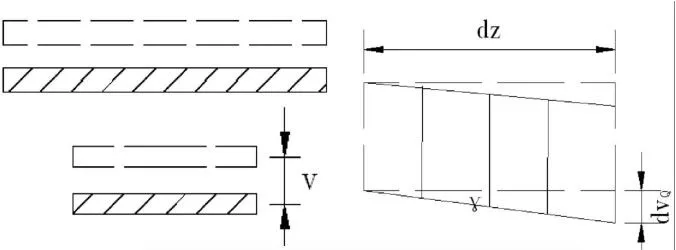
圖2 豎向撓曲位移

豎向撓度V由兩部分組成：由作用于翼板的彎矩M所產生的撓度VM，及作用于波形鋼腹板的剪力Q所產生的撓度VQ。VM可以按照初等梁理論進行計算，而計算VQ時假設截面上剪應力均勻分布，計算圖示如圖2：

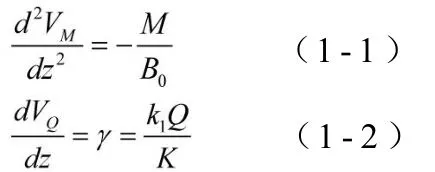
其中，B0為只考慮混凝土翼板面積的截面抗彎剛度，下文簡稱為未折減剛度。如圖2所示，設上、下翼板面積分別為F1和F2，到中性軸的距離分別為h1和h2，忽略翼板截面繞本身形心軸的慣性矩，則：

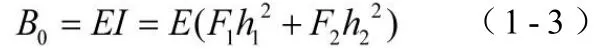
將式（1-1）和式（1-2）代入下式：

其中，B為考慮波形鋼腹板剪切變形的截面抗彎剛度，下文簡稱折減后剛度。

比較式（1-5）和式（1-6）得：

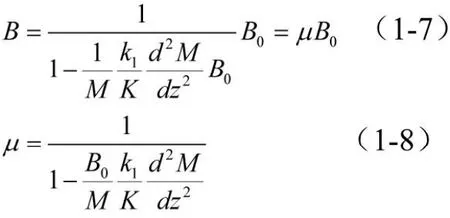
μ為考慮波形鋼腹板剪切變形對截面抗彎剛度的折減系數。

由μ的表達式可以看到，μ與波形鋼腹板抗剪剛度與翼板抗彎剛度之比K/B0有關；μ與波形鋼腹板剪應力分布，即剪應力分布不均的校正系數k1有關。

μ還與截面的彎矩M有關，而彎矩M是坐標z的函數，所以μ也是坐標z的函數；截面截面的彎矩M(z)由約束條件和力邊界條件確定，跨中作用有集中荷載的簡支梁，彎矩M(z)為雙折線；滿跨分布均布荷載的簡支梁，彎矩M(z)為拋物線；分布荷載p(z)為坐標z的一次或者更高次函數，彎矩M(z)將會是三次或者以上拋物線。在分析計算中，每次都根據截面彎矩M(z)來確定μ顯得比較麻煩。鑒于實際荷載為離散隨機分布，截面彎矩M(z)分布規律復雜，在實際分析中，我們可以將截面彎矩M(z)按三角級數進行展開，利用三角函數導數性質，得到μ的實用計算方法：

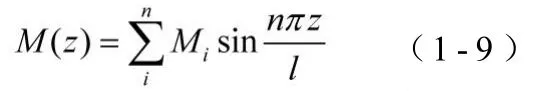
近似取第一項，并令展開彎矩M(z)與實際彎矩在跨中相等，得

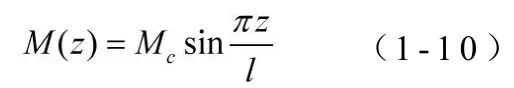
將式（1-1 0）代入式（1-8）得

2 荷載分布差異的影響分析

彎矩M(z)按三角級數進行展開，項數取得越多就能越精確滿足荷載邊界條件，而式（1-11）是只取一項的情況，其不能精確滿足荷載邊界條件，而只能近似等效，實際上，式（1-11）要求荷載邊界應為正弦分布荷載。當荷載為集中荷載或是均布荷載時，式（1-1 1）只能近似的計算，為了說明這種近似計算帶來的誤差在工程中是可以接受，計算結果也是偏于安全的，采用模型進行分析，該模型是文獻[2]的試驗模型。

按照經典梁理論[4]，并引入抗彎剛度折減系數μ，得到簡支梁的荷載、跨中撓度和抗彎剛度三者的關系式為：

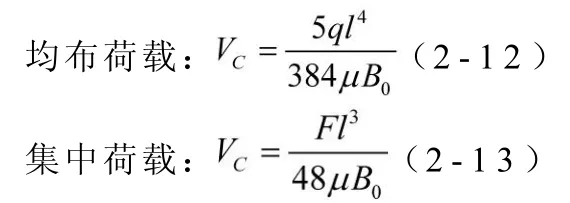
其中B0是只考慮混凝土翼板面積的截面抗彎剛度，為不計腹板剪切變形影響的截面抗彎剛度，下文簡稱為未折減剛度，此時μ =1；

當μ按照式（1-11）計算時，μB0表示考慮波形鋼腹板剪切變形的截面抗彎剛度，也為本文提出抗彎剛度近似計算方法，下文有提到本文方法系按照式（1-11）的近似計算，考慮波形鋼腹板剪切變形的截面抗彎剛度下文亦簡稱為折減后剛度；

提出這樣的假設在試驗或者有限元分析時，荷載、跨中撓度和抗彎剛度總遵循著式（1-1 2）和式（1-1 2）計算格式，剪切變形或者其他影響因素都歸結到抗彎折減系數μ上，B0始終為只考慮混凝土翼板面積的截面抗彎剛度，而不同方法μB0代表的意義就不同。通過試驗可以得到梁的荷載與跨中撓度，將其代入式（1-12）和式（1-12），這樣可以計算出剛度μB0，此時μB0的意義為截面的實際抗彎剛度；有限元分析亦可以得到不同荷載等級下跨中節點的位移，也將其代入式（1-12）和式（1-12）得到有限元的剛度μ B0。

(1) 驗證模型

為文獻[2]的試驗模型。模型尺寸，如圖3所示。波形鋼腹板尺寸：波高為24mm，波長為144mm，斜板段長度32 mm和直板段長度40mm，板厚為2mm，板的高度為307mm。

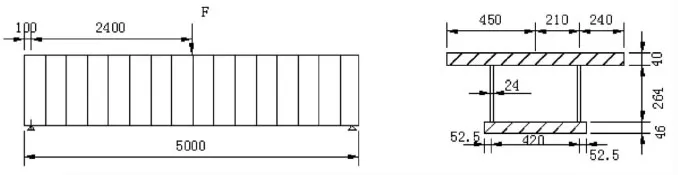
圖3 模型尺寸（單位:mm）

材料性質列于表1。

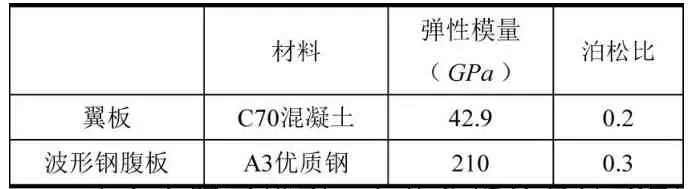
表1 材料性質

建立有限元模型：本節分析的是波形剛腹板剪切變形的影響，單元選擇應能夠保證剪切變形得到正確模擬，shell181可以考慮剪切變形影響的單元，所以采用shell181來模擬波形鋼腹板，而混凝土翼板比波形鋼板厚，采用和shell181同階的實體單元solid45來模擬；不考慮預應力筋作用；利用對稱性，只建立1/ 4模型，在對稱面施加對稱約束即可。模型的約束邊界條件為簡支，所以只約束支座處節點x，y方向的平動自由度，z方向可以自由伸縮；集中力等效為一定面積內分布荷載，以避免應力集中。模型采用映射網格劃分，總共3260個solid45單元，245個shell181單元。圖4為有限元模型。

圖4 試驗模型Ⅰ有限元模型

（a）跨中集中荷載

本節分析波形鋼腹板剪切變形對截面抗彎剛度的折減問題，原則上只要通過式（1-12）和式（1-13）獲得試驗或者有限元模型的抗彎剛度即可，但為了更直觀反映剪切變形影響的規律，我們用未折減剛度和折減后剛度，通過式（1-1 2）和式（1-1 3）計算各荷載等級下不計腹板剪切變形對抗彎剛度折減的撓度值和本文方法計算的撓度值，并將其與有限元法的撓度值、試驗撓度值列于表2進行比較。

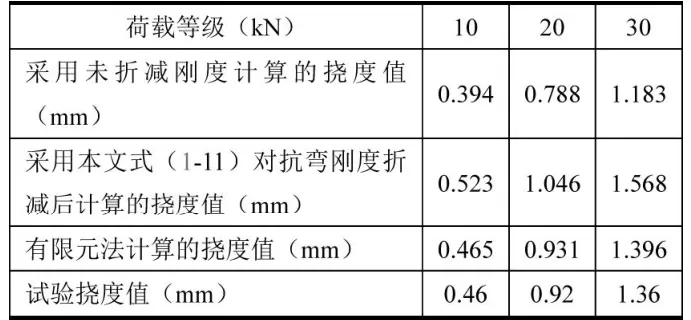
表2 簡支梁受跨中集中荷載的撓度比較

其中，試驗撓度值為文獻[2]的試驗數據。有限元法的撓度值是提取有限元模型跨中底板中間節點和波形剛腹板兩側節點，共三個節點的y方向位移平均值。

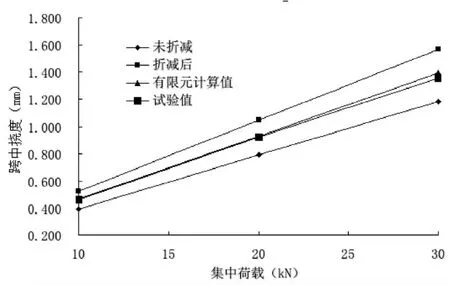
圖5 模型Ⅰ集中荷載—跨中撓度曲線

從圖5荷載—跨中撓度曲線圖可以看出：在試驗荷載范圍內，簡支梁跨中撓度值與荷載是線性關系，說明簡支梁在試驗加載過程中還處于彈性階段；有限元模型計算結果與試驗數據基本吻合。

驗證模型的剪跨比為1/13.7＜1/10，在相同的荷載等級下，剛度未折減的撓度值比試驗和有限元的撓度值偏小，誤差為14.8%，說明在此剪跨比下，波形鋼腹板剪切變形仍引起截面的抗彎剛度較大折減，而忽略剪切變形影響計算得到的截面抗彎剛度偏于剛性。

從式（1-13）看出，截面剛度EI正比于荷載與撓度的比值F/VC，因此，荷載—跨中位移曲線各個直線斜率的比值就是截面的剛度比。取未折減的截面抗彎剛度為1，可以求得折減后剛度為0.757，試驗剛度為0.848，有限元剛度為0.857。將試驗剛度當做簡支梁的實際抗彎剛度，比較折減后截面抗彎剛度與實際抗彎剛度的差值，就可以得到采用式（1-11）近似計算引起的誤差。在集中荷載作用下，驗證模型采用式（1-11）計算折減后剛度比實際抗彎剛度要小10.7%。而未折減抗彎剛度比實際抗彎剛度大17.9%。若不考慮剛度折減，偏于剛性，考慮剛度經折減后，偏于柔性，且誤差值較小，說明此例可采用式（1-11）給出的折減系數計算抗彎剛度。

(b)均布荷載

仍采用試驗模型Ⅰ，將集中荷載轉化為沿垮均勻分布的線荷載，荷載等級分為2.083N/mm，4.166 N/mm，6.249 N/ mm。撓度計算結果列于表3。

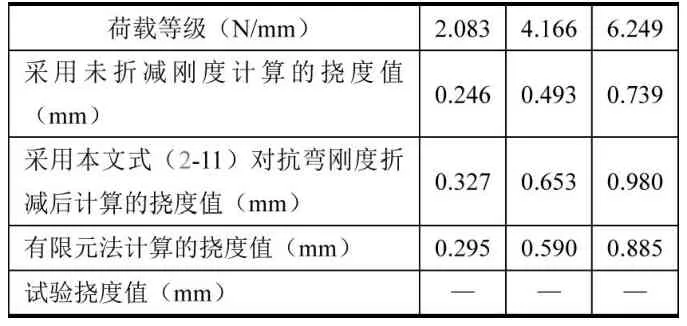
表3 簡支梁受均布荷載的撓度比較

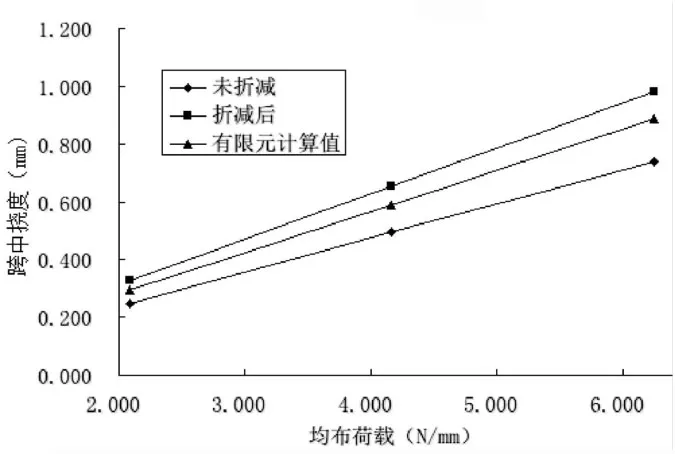
圖6 模型Ⅰ均布荷載—跨中撓度曲線

仍采用前面的方法，取未折減的截面抗彎剛度為1，可以求得折減后剛度為0.754，有限元計算的剛度為0.835。在均布荷載作用下，驗證模型采用式（1-11）對剛度進行折減后比實際抗彎剛度要小9.7%。而未折減抗彎剛度比實際抗彎剛度大19.8%。均布荷載作用下，本例采用式（1-11）計算截面抗彎剛度誤差較小，且結果偏剛性。

從圖5和圖6可以得到可以看出這樣的規律：試驗模型無論是在集中荷載還是均布荷載作用下，未折減截面抗彎剛度偏大，而考慮剪切變形折減后結構剛度偏小，未折減和折減后兩條荷載—跨中撓度曲線包絡著有限元計算得到的荷載—跨中撓度曲線。折減后的曲線與有限元的曲線比較靠近，說明采用式（1-11）給出的折減系數計算抗彎剛度都有較好的精度。

3 結論

本文按照考慮剪切變形的Timoshenko梁彎曲理論推導出，考慮波形剛腹板剪切變形的撓度計算式和剛度計算式，在此基礎上，將彎矩M按三角級數展開并近似取第一項，利用三角函數導數性質，得到簡單的考慮波形剛腹板剪切變形對抗彎剛度折減系數表達式。計算方法最大特點是使用簡單的正弦分布荷載來等效實際復雜隨機的荷載分布，通過驗證模型，驗證了這種等效在集中荷載和均布荷載下具有良好的精度。實際荷載分布具有隨機離散性，其分布引起的內力較集中荷載和均布荷載都要接近于正弦分布規律，或者研究中需要將位移或者內力按照三角級數的情形，計算精度將進一步提高。

[1]水口和之，等.本谷橋的設計與施工.橋梁基礎[M].1998（9）2-10

[2]王文.波形剛腹板箱梁扭轉效應和畸變效應的分析與模型試驗研究[D].湖南大學.2007.5

[3]Mohamed Elg，aaAlynand Sesha，driRobert W.Hamilton Bending Strength of Steel Beams with Corrugated We.bsJ[oJ]urnal of Structural Engineering, Vol.123, No.6, June 1997, pp.772-782

[4]孫訓方，方孝淑，關來泰.材料力學（Ⅰ）[M].北京：高等教育出版社.2001

10.3969/j.issn.1001-8972.2011.12.022

李世深(1984-)，男，工學碩士，廣西崇左市，廣西大學土木建筑學院。