全站儀中間法高差測量的精度分析

楊 云

0 引言

在測量工作中，高差測量是測量的基本工作之一。傳統的高差測量方法包括幾何水準測量、三角高程測量、氣壓高程測量和GPS衛星測高。經典的幾何水準測量精度較高，成果可靠，但工作效率低下;GPS衛星測高需要靜態觀測，經數據處理后精度能夠達到毫米級，出成果周期較長;氣壓高程測量由于精度較低在工程測量中均不會被使用。隨著測量儀器的發展，特別是高精度全站儀的出現，利用全站儀進行三角高程測量，其精度完全可以達到三、四等水準測量，甚至可以達到二等水準測量。

全站儀三角高程測量包括兩種方法:1)在測點上設立測站測高差;2)在非測點設立測站測高差，即工程上稱之為全站儀中間法測高差。這里討論第二種全站儀中間法測高差。

1 全站儀中間法高差測量原理

如圖1所示，在已知高程點A和待測點B上分別安置反光棱鏡，在A，B的大致中間位置選擇與兩點均通視的O點安置全站儀，根據三角高程測量原理，O，A兩點和O，B兩點的高差分別為h1，h2:

其中，S為斜距;α為豎直角;i為儀器高;v為目標高;c為地球曲率影響;γ為大氣折光影響，下標為1的數據指觀測目標A，下標為2的數據指觀測目標B，見圖1。

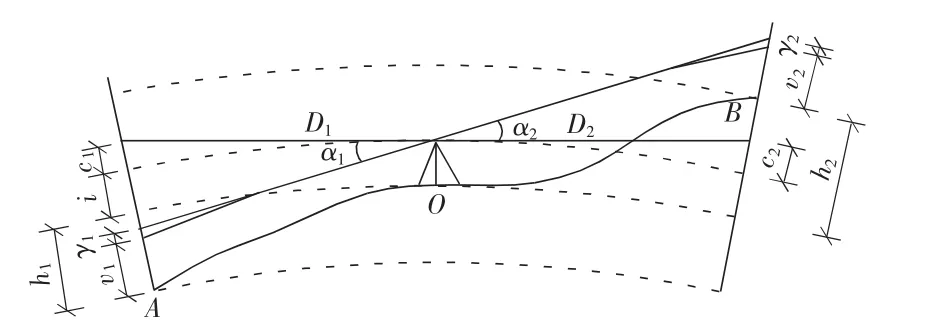
圖1 全站儀中間法高程測量原理

A，B兩點之間的高差hAB:

由式(3)可知，要提高精度，在實際觀測中儀器不動，使用相同高度的目標，兩次觀測的儀器高和目標高分別相等，即相抵消;儀器在安置的時候，盡量的架設在兩觀測點中間，地球曲率影響也可相……