一個非常簡單的排序程序

華晶

北華大學基礎醫學院生物醫學工程教研室，吉林 吉林 132013

一個非常簡單的排序程序

華晶

北華大學基礎醫學院生物醫學工程教研室，吉林 吉林 132013

介紹一非常簡單的排序應用程序。

排序；排序程序；VB程序

把n個任意排列的一組數排序，轉變為從小到大或從大到小排列，這在數據處理中（如統計學處理中的求區分度等）很有用。實際中，有人曾提出過或簡單些或復雜些的排序程序。

筆者提出一個非常簡單的排序程序。

排序思想：比如，把n個任意排列的一組數轉變從大到小排列。先從排列中選出最大的數，作為排列的第一個數；然后再從余下的數中選出最大的數（次最大），作為排列的第二個大數（次最大）；……，如此進行下去，直到結束，則獲取從大到小的排列。

做法如下：以VB代碼排序程序為例。

1．賦值給定義的數組t(n)，如把任意排列的六個數4，5，2，3，1，7賦數組t (n)后，可得t(1)=4，t(2)=5， t(3)=2， t(4) =3， t(5) =1，t(6)=7；

2．選一個比數組中的數都小的數，用變量代碼tx表示之，如令tx=－100；3．編下列二重循環作排序主程序，

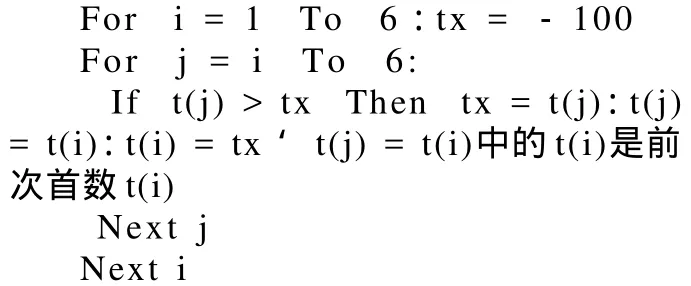
選大數總的做法是：第一重循環 i的數值，對應各次排列首位數的位置，伴隨i=1到6的變化，在第二重循環中，在j=i到6循環中，選出各個最大數tx= t(j)，依次標記為t(i) = tx（i=1，2，3，4，5，6）。在j=i到6的循環中，每當選出大于相應首位數的大數，則把該大數tx = t(j)與此時排在數組相應首位的數t(i)互換位置，其它數位置不動。

分析上述主程序排序過程：以對數組4，5，2，3，1，7作從大到小排列為例。

第一重循環 i=1時，排在首位的數是t(i) = t(j)= t(1) = 4。若各條件t(j) > tx成立，則由第二重循環選出最大數tx =t(j) = t(6) =7，記為t(i) = t(1) = 7。

選出最大數t(i) =t(1)=7的過程如下：

當第二重循環首次排序j=i=1時，有t (j)=t(1)=4（此時首位數是4），然后用條件語句

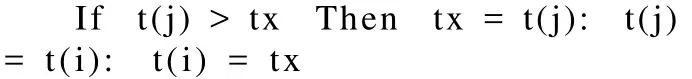
作判斷， 條件 t(j) > tx 成立，即 t(j) =t(1)=4 > tx = －100 成立，則執行tx = t(j)、t(j) = t(i) 及 t(i) = tx，于是由tx = t(j)得到從tx=－100 轉換為tx= t(j)= t (1)=4，tx=4為初次選出的大數。之后執行位置互換 t(j) = t(i) 及t(i) = tx，即由t(j) = t(i)知， t(j) = t(1)=4 與t(i) = t(1) =4互換位置。但因此時t(j) = t(1)與t(i) = t(1)數值相同（均為4），屬同一位置的數，可見該次排序中，數組中原先各數位置沒變，仍為4，5，2，3，1，7（請記住此時tx=4）；

每次第二重循環開始進行首次排序（j=i）時，數組均維持前邊的排列不變。

當第二重循環中的j=2時，有t(j)=t(2) =5，條件t(j) > tx成立，即t(j) = t(2) =5> tx=4成立，于是選出大數tx= t(j)=t (2)=5。之后執行位置互換t(j) = t(i) 及 t (i) = tx，由t(j) = t(i) 知，t(j) = t(2)=5被前次t(i) = t(1) =4替換，變為t(j) = t (2) =4，于是前次排列數組中第二個數5被換為原排在首位的數4。由后一轉換t(i) = tx知，選出的大數t(i) = t(1)= tx=5被換到首位，形成排列中第二個數5與原首數4的位置互換，其它數的原位置不變，于是原排列4，5，2，3，1，7變為5，4，2，3，1，7（請記住此時tx=5）；

可見，滿足條件t(j) > tx則作位置互換，選出的大數被換到此刻數組首位。

當第二重循環j=3，4，5時，有t(j)= t (3)=2，t(j)= t(4)=3、t(j)= t(5)=1條件t(j) > tx=5不成立，故不執行t(j) = t(i) 及t (i) = tx位置互換，數組仍為前次排列5，4，2，3，1，7；

可見，不滿足條件t(j) > tx時，各數排列位置不變，維持前一次排列。

當第二重循環j=6時，有t(j)= t(6)=7，條件t(j) > tx成立，即t(j)= t(6)=7> tx=5成立，

于是執行tx= t(j)、t(j) = t(i) 及 t(i) = tx。由tx= t(j)選出大數tx= t(j)= t(6) =7。作位置互換t(j) = t(i) 及 t(i) = tx，有t(j)= t(6)=7被換到前次排列t(i) = t(1) = tx=5的位置（首位），而前次排在首位的數5被換到t(j)= t(6)的位置，排列5，4，2，3，1，7變為7，4，2，3，1，5。

至此，第一重循環第一步（i=1）結束，選出最大數7，并用此時t(i) = t(1) = tx=7標記。

第一重循環進行第二步，即 i=2時，重定tx=－100，并仍由第二重循環選出數組中的大數，即選出原數組中的第二最大數tx =5，并記為t(i) = t(2)= 5。

因此時第二重循環由j=i=2，取到j=6，故第二大數是去掉前次排在首位的大數7以后的數組中選，即在4，2，3，1，5中選，故此數組的首數是4。

第二大數5選出過程如下：

當第二重循環j=2時，條件t(j) = t(2) =4 > tx=－100成立，執行tx=t(j)、 t(j) = t(i)及t(i) = tx。此時選出大數tx=4，類似上述i=1時的分析，故排列4，2，3，1，5沒變，總排列仍是7，4，2，3，1，5。其實，這是第二重循環第二次作首次排列，故排列應維持前次排列不變。

當j=3，4，5時，分別有t(j)= t(3) =2，t(j)= t(4) =3，t(j)= t(5) =1，條件t(j) > tx=4不成立，排列不變（請記住此時仍是tx=4）。

當j=6時，有t(j)= t(6)=5，條件t(j) = t(6)=5> tx=4成立，選出大數tx= t(j) = t(6)=5。之后作位置互換，由t(j) = t(i)知，t(j)= t(6)= 5被換為前次t(i) = t(2)= tx=4，即換為t(j)= t(6)= 4，由t(i) = tx知，t(i) = t(2)= tx =5（此次tx = 5），于是有5與排在首數4互換位置，排列由4，2，3，1，5變為5，2，3，1，4，總排列由7，4，2，3，1，5變為7，5，2，3，1，4。

至此，第一重循環第二步（i=2）結束，選出次大數5，并用此時t(i) = t(2) = tx=5標記。

如此進行下去，每當滿足條件t(j) > tx時，就有位置互換，把各次選出的最大數換到前邊相應的各個次最大數的位置，直到取完i=1到6及j=i到6，完成兩重循環，獲取從大到小的排列7，5，4，3，2，1。

源程序如下：

For i=1 To 6: Print t(i) , ： Next i ‘顯示從大到小排列后的數組

運行程序結果：顯示出原排列為：4，5，2，3，1，7

從大到小排序為：7，5，4，3，2，1

由上述知，選最大數tx = t(j)及排序動作t(j) = t(i) 及 t(i) = tx只有滿足條件t(j) > tx時才發生，且只有互換位置動作，因此，程序運行過程的步驟少。

此排序程序比某些排序程序（有很多）運行步驟少得多、簡單得多。

改變程序中條件語句的大于號為小于號，并令tx=100, 可得從小到大排序。

[1]劉娜,鄭楠楠.插入類排序算法的改進及實際應用.沈陽大學學報2008;2:14～18

[2]吳奇英.計算機程序設計中的排序方法.交通科技與經濟2007;4:74～76

[3]姜曉銘主編.Visual Basic 6.0中文版編程指南.第1版:中國石化出版社2006;5

10.3969/j.issn.1001-8972.2011.24.047

華晶，工程碩士，實驗師。