B?cklund變換下一類Burgers方程精確解分析
王理凡
(金華職業技術學院,浙江 金華 321007)
B?cklund變換下一類Burgers方程精確解分析
王理凡
(金華職業技術學院,浙江 金華 321007)
形如ut=F(u,ux,uxx)的非線性偏微分方程由可積系統vx=P(v,u,ux),vt=Q(v,u,ux)定義的B?cklund變換u→v分類, 其最簡Burgers方程為ut=uxx+2uux,相應的可積系統是vx=(λ+v)(u-v),vt=(λ+v)(u2-ux-uv)-λ(λ+v)(v-v),其中,λ是任意常數。將B?cklund變換連續n次作用于Burgers方程的零解u0(x,t)≡0, 并且每次取不同的參數λk(1≤k≤n), 得到了Burgers方程的精確解un(x,t),并揭示了Burgers方程光滑和(或)奇異扭結解相互作用的過程。
B?cklund變換;可積系統;Burgers方程;扭結解
非線性微分方程在物理學、工程學中都有著廣泛的應用,特別是可用于描述帶有非均勻邊界條件的物理背景中的各種非線性波動現象的動力學機制。B?cklund變換現已成為求解某些非線性偏微分方程的有力工具,是可積系統方面的一個重要研究領域。文獻[1]研究了形如:
ut=F(u,ux,uxx)
(1)
的非線性偏微分方程由可積系統:
vx=P(v,u,ux)vt=Q(v,u,ux)
(2)
定義的B?cklund變換u→v的分類,證明了這樣的非線性偏微分方程只能是Burgers方程:
ut=uxx+2uux
(3)
相應的可積系統是:
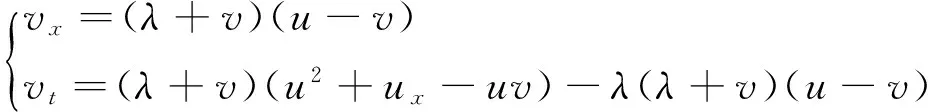
(4)
下面,筆者將在以上研究的基礎上,將B?cklund變換反復作用于Burgers方程的零解,從而得到Burgers方程的許多精確解,進而分析Burgers方程光滑和(或)奇異扭結解相互作用的過程, 并通過部分圖形描述、分析非線性波動現象。
設u為Burgers方程(3)的一個解,則由可積系統(4)的第1個方程可得:

(5)
式中,c(t)是積分常數。將式(5)代入系統(4)的第2個方程可以得到函數c(t)所滿足的常微分方程, 由該常微分方程的解即可得到Burgers方程的解。
結果1將u0(x,t)≡0代入系統(4)并取參數λ=λ1可得Burgers方程的解:

(6)
注1u1是行波解。當參數λ1>0時,它是一個光滑扭結,而當λ1<0時,它是一個奇異扭結。
例1當λ1=1時,u1是一個光滑扭結;當λ1=-1時,u1是一個奇異扭結(見圖1) 。
結果2將u1(x,t)代入(4)并取參數λ=λ2可得Burgers方程的解:

(7)

圖1 光滑扭結(左)和奇異扭結(右)
注2u2可看成是2個光滑和(或)奇異扭結的相互作用,共有以下3種情形:①u2若是2個光滑扭結相互作用的過程,結果是1個光滑扭結;②u2若是1個光滑扭結與1個奇異扭結的相互作用,結果是1個奇異扭結;③u2若是2個奇異扭結相互作用的過程,結果也是1個光滑扭結。
例2當λ1=-2,λ2=-1時,u2就是2個奇異扭結相互作用的過程,結果是1個光滑扭結(見圖2)。
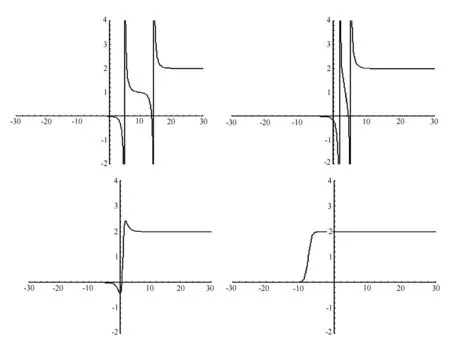
圖2 2個奇異扭結的相互作用過程
結果3將u2(x,t)代入(4)并取參數λ=λ3可得Burgers方程的解:

注3u3可看成是3個光滑和(或)奇異扭結解的相互作用, 共有以下6種情形:①u3若是3個光滑扭結的相互作用,結果是1個光滑扭結; ②u3若是1個光滑扭結和2個奇異扭結(光滑扭結位于2個奇異扭結之間)的相互作用,結果是1個光滑扭結;③u3若是另外一種1個光滑扭結和2個奇異扭結(2個奇異扭結為鄰)的相互作用,結果也是1個光滑扭結;④u3若是1個奇異扭結和2個光滑扭結(2個光滑扭結為鄰)的相互作用,結果是1個奇異扭結;⑤u3若是另一種1個奇異扭結和2個光滑扭結(奇異扭結在2個光滑扭結之間)的相互作用,結果也是1個奇異扭結;⑥u3若是3個奇異扭結的相互作用, 結果也是1個奇異扭結。
例3當λ1=-3,λ2=-2,λ3=-1時,u3就是3個奇異扭結的相互作用,結果是1個奇異扭結(見圖3)。

圖3 3個奇異扭結的相互作用過程
一般地, 將B?cklund變換連續n次作用于Burgers方程的零解u0(x,t)≡0, 并且每次取不同的參數λk(1≤k≤n),則可得到Burgers方程的解un(x,t), 它可看成是n個(光滑和(或)奇異)扭結的相互作用。不管這n個扭結的相對位置如何, 當奇異扭結的個數是偶數時,作用的結果是1個光滑扭結;而當奇異扭結的個數是奇數時,作用的結果是1個奇異扭結。
[1]王理凡.一類二階非線性偏微分方程B?ecklund變換的分類[J].浙江大學學報(理學版),2011,38(1):19-21.
[2] Cao X, Wu H, Xu C.On Miura transformations among nonlinear partial differential equations[J]. J Math Phys, 2006,47 :083515.
[3] Byrnes S G.B?cklund transformations and they equation [J]. J Math Phys,1976,17: 836-842.
[4] Mclaughlin D W, Scott A C.A restricted B?cklund transformationszx=F(x,y,z)[J].J Math Phys, 1973,14:1817-1828.
[5] Nimmo J J C, Crighton D G.B?cklund transformation for nonlinear parabolic equations[J]. Proc R Soc London, 1982,384:381-401.
[6] Oliver P J.Applications of Lie Groups to Differential E quations[J]. New York :Springer-Verlag, 1993.
[7] Wu H. On B?cklund transformations for nonlinear partial differential equations[J].J Math Anal Appl, 1995,192:151 - 179.
[編輯] 洪云飛
10.3969/j.issn.1673-1409.2011.03.002
O175.29
1673-1409(2011)03-0004-03

