2n+2階完美幻方的二進制構造法及其計數

曹小琴

(金華教育學院數學系,浙江金華 321000)

2n+2階完美幻方的二進制構造法及其計數

曹小琴

(金華教育學院數學系,浙江金華 321000)

利用二進制構造出2n+2階和諧方,由此給出一類“0～22n+4-1”域上的2n+2階完美幻方,這類幻方共有26n+4×(2n+4)!個.

完美幻方;構造法;和諧方

完美幻方,也叫泛對角線幻方,或叫純幻方,是指n階數字方陣,它的各行(列)和、各泛對角線和均相等.

二進制是非常奇妙的,它在幻方中的應用更是獨特.文[1]利用二進制構造了4階泛對角線幻方的統一公式,文[2],[3]分別給出了4n階幻方的一種構造法.本文利用二進制的特點構造一類2n+2階(n為非負整數)完美幻方,數量極其豐富,共有26n+4×(2n+4)!個.如這類8階完美幻方共有210×6! =737280個.當n=0時此構造法(定理1)得到所有4階完美幻方.

為討論方便,定義幾個概念.記

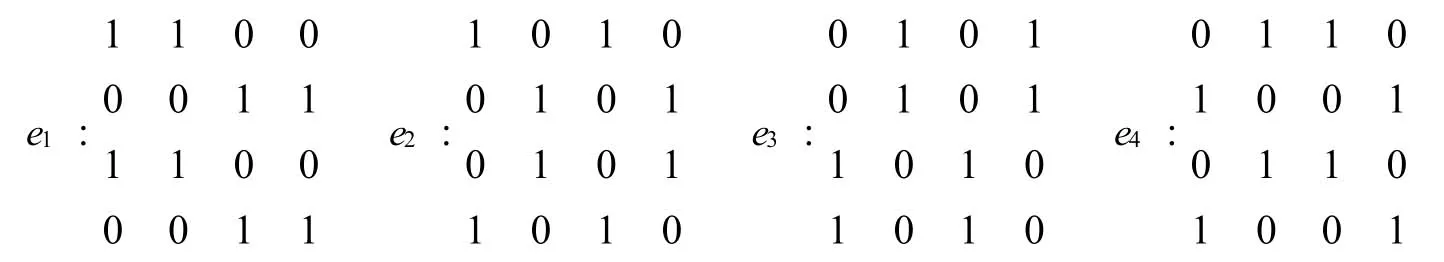
i=1,2,3,4,ei每位元素加1(mod 2)的方陣(稱為模2加1方陣)記為.記

ei和Bi,B′i,B″i均具有相同的特點.

定義1 若由“0,1”兩元素組成的2n+2階方陣滿足：各行(列)、各泛對角線的4×2n+2組數中,每一組均有相同個數的0和1,把這類(0,1)方陣,簡稱2n+2階和諧方.

顯然,若一方陣是和諧方,那么它的模2加1方陣也是和諧方.i=1,2,3,4,ei和Bi,B′i,B″i(及它們的模2加1方陣)分別為4階和8階和諧方.

定義2 若一完美幻方已轉化為二進制,則稱此完美幻方為二進制下的完美幻方.

任一0～22n+4-1的自然數均可表示成2n+4位二進制數,此域上的任一2n+2階二進制下的完美幻方滿足：各行(列)、各泛對角線的4×2n+2組數中,每組中每位均有2n+1個0和2n+1個1(因為幻和等于2n+1(22n+4-1)=2n+1(1+21+22+…+22n+3)).反之亦然.如各元素按順序B3,B4,,,B″3, B′3結合成的8階方陣為二進制下的完美幻方.

定義3 n×n方陣,我們把左上(右上)右下(左下)的主(次)對角線稱為主(次)0對角線,往下的各折對角線依次稱為主(次)1,主(次)2,…,主(次)n-1對角線.

1 2n+2階和諧方的構造

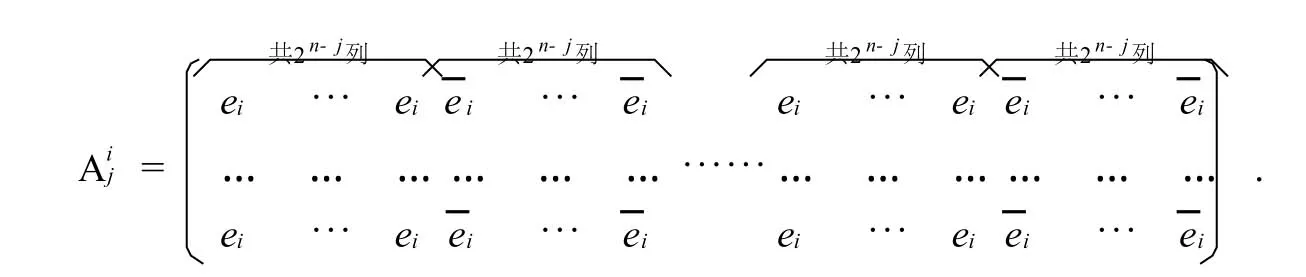
大括號內共有2j大組,2n行,A的轉置方陣記為B(j=1,2,…,n;i=1,2,3,4).

引理1,(j=1,2,…,n;i=1,2,3,4)及它們的模2加1方陣均為和諧方.

證先證A(j=1,2,…,n)為2n+2階和諧方.

(i)主4k[主4k+1;主4k+2;主4k+3](k=0,1,2,…,2n-1)對角線上有2n-1組(1,0,0,1) [(0,1,1;0);(1,0;0,1);(0;1,1,0)]和2n-1組(0,1,1,0)[(1,0,0;1);(0,1;1,0);(1;0,0,1)],從而有2n+1個0和2n+1個1.

(ii)各次對角線從右上至左下的數與各主對角線從左上至右下的數的排列分別完全相同,從而也有相同個數的0和1.

2 2n+2階完美幻方的構造

引理2 由e1,e2,e3,e4或任取其中i(0≤i≤4)個,其余4-i個方陣取模2加1,把它們按任意順序結合成的4階方陣D,16個元素互不相同,且為0000～1111.

證(i)e1,e2,e3,e4及它們的模2加1方陣均為4階和諧方.

(ii)D的各行(列)、各泛對角線的4個數,每位均有兩個0和兩個1.

(iii)D的16個元素一定互不相同.若不然,假設有兩元素相同,(共有6種可能：1100;1010;1001; 0110;0101;0011.)不妨設1010,1010(其余5種情況同理可證),它們一定出現在16組數的某一組中,不妨設第1行,由(ii)可知,其余兩數必為0101和0101,分解后的4個和諧方第1行為(1,1,0,0), (0,0,1,1),(1,1,0,0),(0,0,1,1),顯然它們不是由“e1,e2,e3,e4或任取其中i個,其余4-i個方陣取模2加1”得到的,因而這16個數兩兩不同.顯然最小和最大數分別為0000和1111.

引理3 i=1,2,3,4,,,…,中各任取一個;,,…,中各任取一個.在這2n個和諧方中任取t(0≤t≤2n)個,其余2n-t個方陣取模2加1,按任意順序結合得到的2n階方陣各元素均不同.

證由(j=1,2,…,n;i=1,2,3,4)的構造可知,2n階方陣A及它的模2加1方陣左右兩半元素不同;及它的模2加1方陣把左右兩半各等分為不同的兩半,…,因而(i)(AA),(A), (A),()(i,u=1,2,3,4)均分為不同的4個大列;…;(AA…A)2n列的元素各不相同(考慮順序).(ii)同理,它們的轉置方陣2n行的元素各不相同.則(AA…ABB…B)(或其中若干個方陣取模2加1,或按其它順序排列)(i,u,l,i′,u′,l′=1,2,3,4)組成的2n階方陣中的各元素(考慮順序)一定不同.因為：某行任取一元素,某列任取一元素,若這兩元素在同一行(列),由(i)((ii))可知,這兩元素的2n位上B(A)對應位的元全同,A(B)對應位的元不全同,因而這兩元素不同;若這兩元素既不在同一行又不在同一列,A,B對應位的元都不全同,因而這兩元素也不同.

定理1 A,A,…,A中各任取一個;B,B,…,B中各任取一個.在這2n個和諧方及C1～ C4中任取s(0≤s≤2n+4)個,其余2n+4-s個方陣取模2加1,把它們按任意順序結合成的2n+2階方陣F(把ei數值代入)為二進制下的2n+2階完美幻方,對應于十進制為“0～22n+4-1”域上的完美幻方,此類幻方共有26n+4×(2n+4)!個.

證(i)A,,…,(i=1,2,3,4)中各任取一個,B,B,…,B中各任取一個;在這2n個和諧方及C1～C4中任取s(0≤s≤2n+4)個,其余2n+4-s個方陣取模2加1;把它們按任意順序結合成的2n+2階方陣為F.

(ii)由引理2,3可知組成的2n+2階方陣F中各元素均不同,最小數為00…0,最大為11…1(2n+4位數),對應于十進制為0～22n+4-1.

F為2n+2階完美幻方.因為F中各行(列)、各泛對角線的2n+2個數(每一數均為2n+4位二進制數)中,每位均有2n+1個0和2n+1個1,因而F中各行(列)和、各泛對角線和均等于2n+1(1+2+22+…+22n+3)=2n+1×(22n+4-1).

(iii)相同和諧方任意兩種不同排法得到的兩個完美幻方一定不同;不同和諧方的任意兩排列得到的兩完美幻方也不同.若得到兩個相同的完美幻方,則二進制下的兩個完美幻方也相同,因而分解后的和諧方為同一組的相同排列,矛盾.

注 當n=0此構造法得到所有4階完美幻方(16×4!=384個).

3 n=2的一個實例

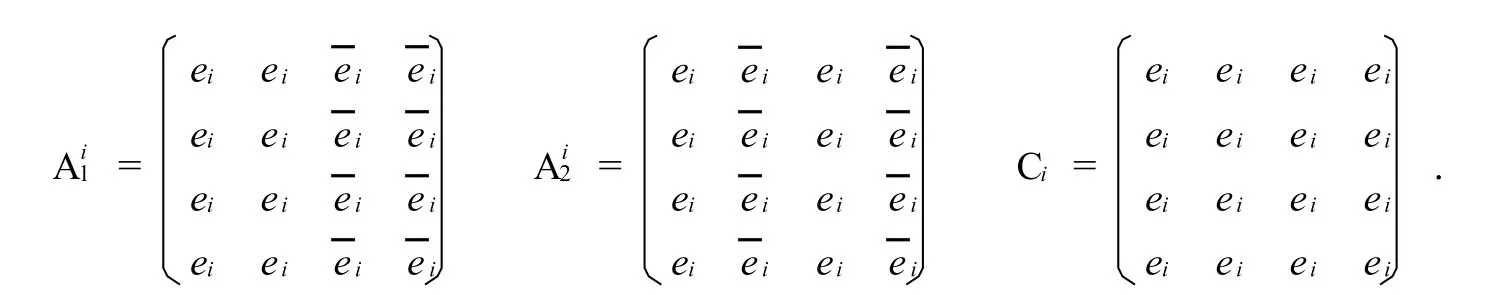
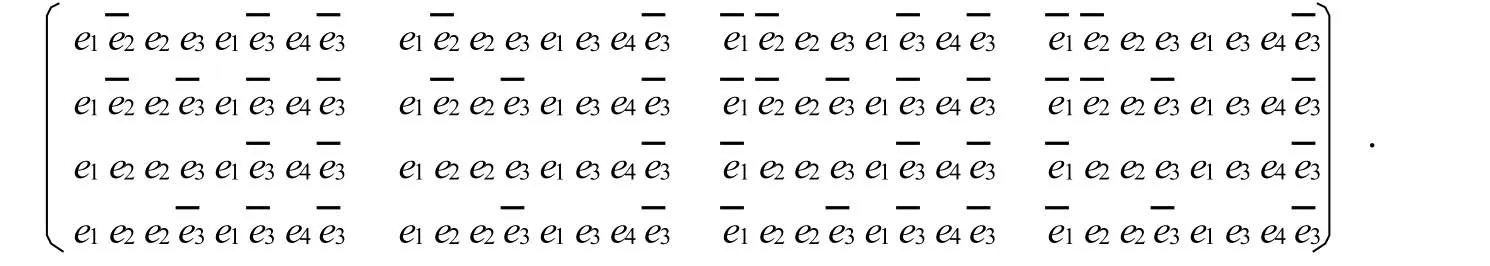
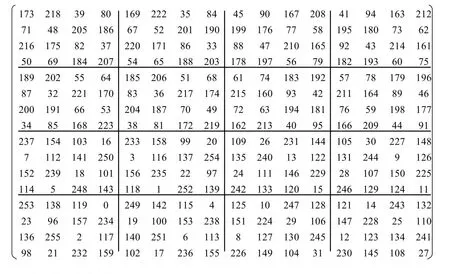
分別把e1,ˉe1,e2,ˉe2,e3,ˉe3,e4的4階和諧方代入上式,得到二進制下的16階完美幻方,轉化為十進制即得“0～255”上的16階完美幻方G：

[1] 潘鳳雛.構造所有4階泛對角線幻方的統一公式[J].大學數學,2005,21(3)：74-76.

[2] 曹小琴.4n階完美幻方的新構造法[J].寧夏大學學報,2001,22(1)：11-14.

[3] 俞萬禧.一種4n階幻方構造方法的論證[J].數學的實踐與認識,2004,34(2)：85-89.

Binary Constructing Method of Perfect Magic Square of 2n+2Orders&Its Counting

Cao Xiao-qin
(Mathamatic Department of Jinhua Institute of Education,Jinhua,Zhejiang 321000,China)

In this article the author constructs abalance square of 2n+2orders by using binary cell and from this a kind of perfect magic squares of 2n+2orders are created on the field of“0～22n+4-1”.The total number of the magic square is 26n+4×(2n+4)!.

perfect magic square;constructing method;balance square

O157

A

1672-1454(2011)03-0098-04

2008-08-11;[修改日期]2008-12-04