基于灰色Verhulst優化模型的裝備研制費用高精度預測

劉光軍，柯宏發，劉嘉文

(1.總裝備部 通信網絡管理中心，北京100720;2.裝備學院，北京101416)

1 引言

武器裝備全壽命周期費用技術受到了越來越廣泛的重視［1，2］，對武器裝備系統研制費用進行預測，可為國防預算的節省，新武器裝備系統的論證、研制、生產、使用和保障等全壽命管理提供可靠的依據［3］。針對裝備研制費用預測問題，小樣本問題和新型智能優化算法是目前的研究熱點，如文獻［2］將神經網絡引入到灰色Verhulst模型來提高研制費用預測精度，文獻［3］建立了基于粗糙集的RBF神經網絡裝備研制費用預測模型。從實際工程背景來看，裝備研制遵循方案論證、初樣設計研制、正樣設計研制、靶場試驗、定型等工作程序;大部分裝備研制費用隨著時間的推移，經費需求初期少，中期的某一時期達到高峰，后期又減少，研制費用累積曲線呈S型變化特征［4］。灰色Verhulst模型是一種很廣泛的動態預測模型，是S型小樣本數據列建模的有效工具，在軍事裝備研制費用預測領域取得了廣泛的應用，如文獻［4］利用灰色Verhulst模型對魚雷研制費用進行了建模。

但是灰色Verhulst模型是有偏差的灰指數模型，在應用過程中存在模擬預測精度不高的情況，對其改進方法的研究也是灰色理論與應用研究的熱點問題之一［5，6，7，8，9］。如文獻［7］提出了以x(1)(n)作為初始條件的建模方法，文獻［8］提出了以殘差進行修正來提高灰色Verhulst模型的建模精度。

本文認為初始數據列系統是動態變化發展的，背景值的構造形式和初始條件的選取是相互影響的，考慮背景值優化和初始條件優化之間的誤差積累傳播，提出了基于數學規劃的灰色Verhulst模型優化方法，介紹了應用模擬退火算法求解該模型。通過對模擬數據的比較分析發現，應用本文所提出的灰色Verhulst優化模型來對裝備研制費用進行建模，比文獻［4］、文獻［8］有更高的模擬精度，并與原始數據列具有更大的灰關聯度。

2 灰色Verhulst模型及其求解

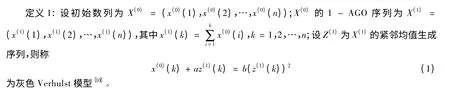
命題1(證明略):灰色Verhulst模型x(0)(k)+az(1)(k)=b(z(1)(k))2中待估計參數a為模型的發展系數，待估計參數b為模型的灰作用量，另設^a=(a，b)T為參數列，且設

在實際建模過程中，可以取初始序列為X(1)，其1階累減生成序列為X(0)，建立灰色Verhulst模型直接對X(1)進行模擬。

3 灰色Verhulst優化模型

3.1 基于數學規劃的灰色Verhulst優化模型

Verhulst模型主要用來描述非單調擺動發展或具有飽和狀態的過程，即S形過程，最初慢慢上升，然后迅速增長，最后慢慢趨于極限，常用于人口預測、生物生長、繁殖預測和產品經濟壽命預測等。建立灰色Verhulst模型的實質就是通過建模得到初始序列的擬合曲線，從擬合預測的角度出發，則希望最終的模擬序列能夠最優地逼近初始序列，并且能具有較高的預測精度。由上節建模過程可以看出，模擬序列的建模精度取決于背景值逼近精度和初始條件常數c的精度。

定義1中Z(1)的緊鄰均值生成是一種平滑處理，當時間間隔很小、序列數據變化平緩時，這樣構造的背景值是合適的，模型偏差較小;但當序列數據變化急劇時，這樣構造出來的背景值往往產生較大的滯后誤差，模型偏差較大，因而在一定程度上會影響預測精度。另外，以數據表征的各種系統是動態變化的，因此以固定的背景值構造形式應用于所有系統也是不合適的。根據灰色系統的新信息有限原理，在進行背景值的構造時可以考慮新舊信息的相對重要性，本文采用下述背景值加權構造形式，即:

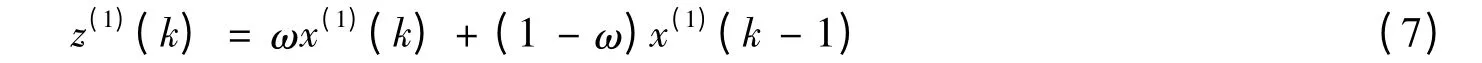
式(7)中，ω為新信息的加權權重，針對不同的系統進行優化求解。灰色Verhulst模型本身是一個模擬預測模型，如果以系統的當前預測點為原點，在該原點之前，越遠離原點數據的信息意義將逐步降低，再進行Verhulst模型預測的意義就越弱，越靠近原點的數據信息更能反映系統的目前特征，所以在進行建模時考慮數據的相對重要性顯然是合理的。

針對初始條件常數c的優化，強行令初始值為x(1)(1)來推導常數c缺乏嚴格的理論依據，使得解出的灰色Verhulst模型不一定是最佳預測公式;另外令初始值為x(1)(n)來推導常數c，由于x(1)(n)是由原始序列累加生成的，原始序列的信息通過x(1)(n)都可以得到充分反映，因此把它作為初始條件符合灰色系統理論新信息優先原理，也符合灰色系統理論最少信息原理，有可能使模型的預測精度比原模型的預測精度得到提高，但是不能保證與原始數據列保持最好的動態發展趨勢。由上節建模過程可以看出，背景值的構造形式對常數c的求解是有影響的，也就是說，背景值優化帶來的偏差會影響初始條件常數c優化。于是，基于背景值優化和初始條件優化之間的誤差傳播累積作用，針對任意的加權權值ω下，本文考慮模擬值與原始值的相對誤差平方和最小的目標來優化確定常數c，其相對誤差平方和ΔEω為:

將c代入式(5)，求得^x(1)(k)，它是ω和c的函數。于是得到灰色Verhulst參數優化的數學規劃模型:

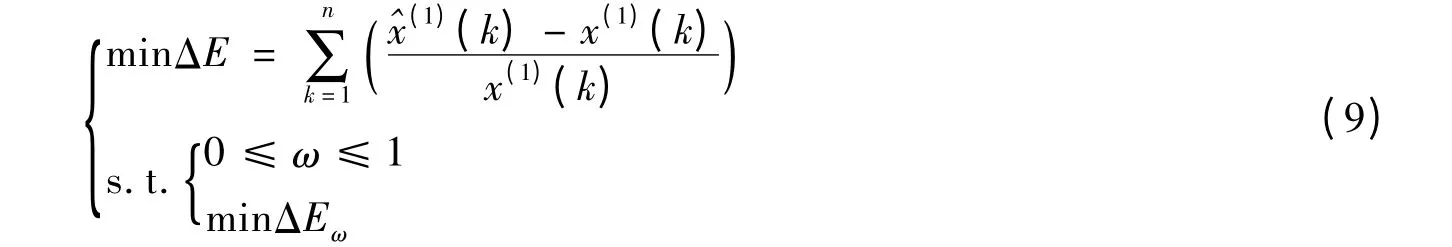
求解該模型得到最優的ω、發展系數a、灰作用量b和初始條件常數c，根據式(5)即可求得灰色Verhulst模型的最優模擬時間響應序列。該模型中ΔE和ΔEω都是非線性函數，本文選用模擬退火算法進行求解。

3.2 灰色Verhulst優化模型的模擬退火算法

模擬退火算法，就是模擬固體退火過程的一種組合優化算法，在求解過程中不但接受對目標函數改善的狀態，而且還以某種概率接受使目標函數惡化的狀態。算法由一個控制參數T決定，經過大量解變換后，可求得給定控制參數下優化問題的相對最優解;然后緩慢減小參數T的值，重復迭代過程，當參數T趨于0時，系統狀態對應于優化問題的全局最優解。這種算法的特點可以使之避免過早收斂到某個局部極值點，從而能夠比較有效地進行全局搜索最優值。

3.3 模型擬合的有效性分析方法

對灰色Verhulst模型進行優化的目的是使得最終的擬合曲線能夠最優地逼近初始序列曲線，因此需要考察灰色Verhulst模型擬合的模擬序列與初始序列X(0)的接近性與相似性。灰色系統理論中灰色關聯分析的實質就是比較數據到曲線幾何形狀的接近程度，一般來說，幾何形狀越接近，變化趨勢也就越接近，灰關聯度就越大。因此，本文利用模擬數據列與X(0)的灰色關聯度大小來比較分析擬合的有效性，兩者的灰色關聯度越大，表示擬合曲線與系統曲線X(0)越接近，幾何形狀越相似，用序列來模擬序列X(0)越有效。

在進行灰關聯分析時，以初始序列X(0)作為參考序列，然后求得各種模擬數據列與X(0)的灰色關聯度，進而根據灰色關聯度的大小進行判斷即可。數據列與X(0)的灰色關聯度用γ(，X)表示，有算式:

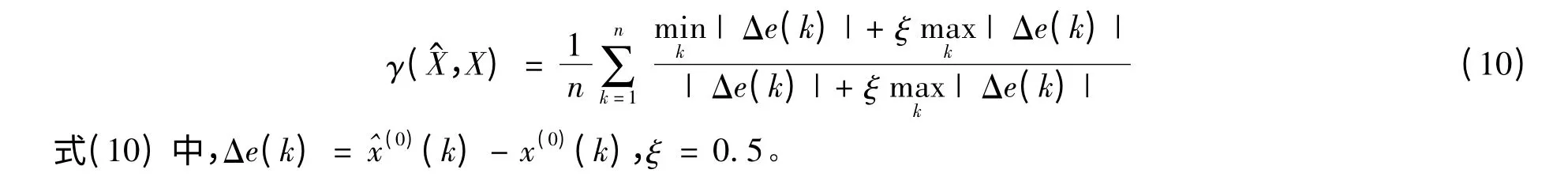
4 魚雷研制費用算例驗證

以文獻［4］提供的魚雷研制費用數據為例進行灰色Verhulst優化模型建模，魚雷逐年研制費用和累積研制費用見表1。

表1 魚雷逐年和累積研制費用(萬元)

應用本文灰色Verhulst優化模型，求得最優的ω=0.4，其模擬時間響應式為:

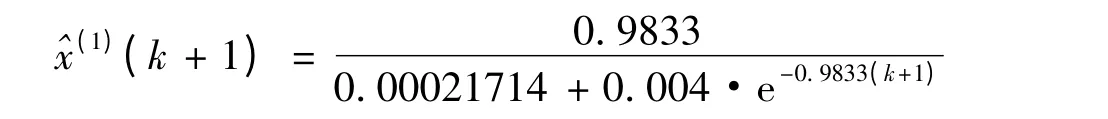
將該模型模擬結果和文獻［4］、文獻［8］的模型進行比較與分析。分別計算各模型的模擬數據，并將相應的實際數據、模擬數據、相對誤差和平均相對誤差列于表2。

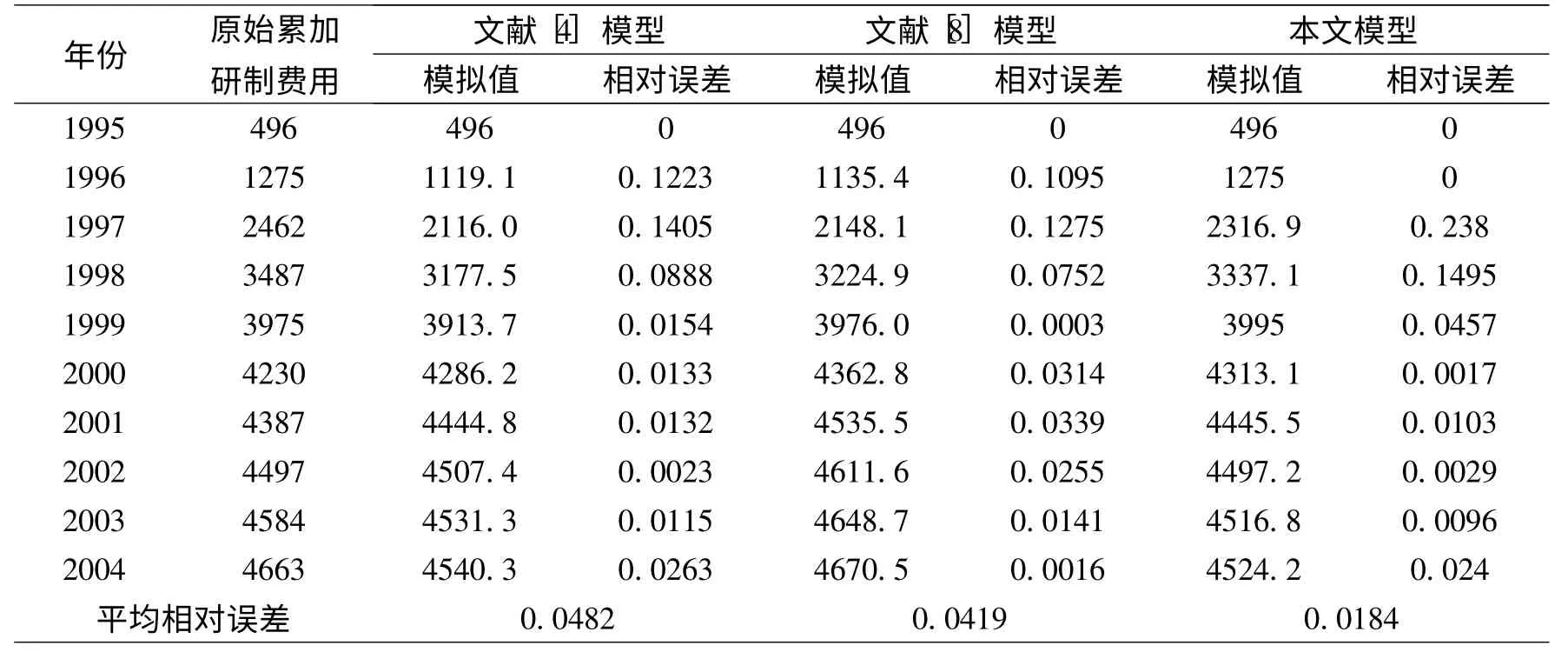
表2 各種模型的模擬精度比較

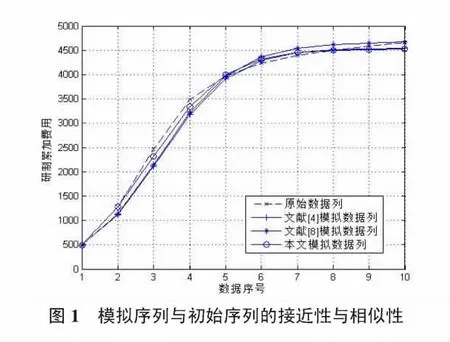
由表2可以看出，本文提出的灰色Verhulst優化模型的平均相對誤差最小。假設X(0)代表原始數據列，分別代表文獻［4］模型、文獻［8］模型和本文模型的模擬數據列，各數據列曲線如圖1所示。圖中以虛線表示原始數據列，很直觀地就可以看出，本文灰色Verhulst優化模型所得的模擬序列與原始序列的接近性與相似性最好，其模擬性能最優。

考察上述三種模型所得的模擬數據列與原始序列X(0)的灰關聯度，基于式(10)求得=0.6755、γ(=0.6692和γ=0.7673，本文灰色Verhulst優化模型所得的模擬序列與原始序列的灰關聯度最大，模擬預測性能最優。

5 結束語

裝備研制費用的預測是武器裝備全壽命管理中一項很重要的工作，本文提出了基于數學規劃的灰色Verhulst優化模型，有效地解決了小樣本裝備研制費用預測問題，并且較好地提高了預測精度。大量數據仿真結果表明，本文所提模型也適用于其它呈S型特征的數據列預測問題。針對多峰值的研制費用預測問題［2，4］，基于本文模型如何實現高精度預測值得進一步研究。

1 郭繼周，宋貴寶，彭紹雄.裝備使用保障費用灰色建模分析［J］.系統工程與電子技術，2004，26(1):64-67.

2 劉建永，李凌，伍中軍.基于神經網絡灰色Verhulst算法的裝備研制費用預測模型［J］.解放軍理工大學學報(自然科學版)，2008，(4):335-338.

3 孟科，張恒喜，李登科，等.基于粗糙集的RBF神經網絡在裝備研制費用預測中的應用［J］.裝備指揮技術學院學報，2006，17(5):14-17.

4 梁慶衛，宋保維，賈越.魚雷研制費用的灰色Verhulst模型［J］.系統仿真學報，2005，17(2):257-258.

5 ZHAO ZHONGMING，CHEN XIEN.Surface Movement and Deformation Simulated by Verhulst Model［C］//Proceedings of 2009 2nd IEEE International Conference on Computer Science and Information Technology，Beijing，2009:459-461.

6 ZHAO WENQING，ZHU YONGLI.A Prediction Model for Dissolved Gas in Transformer Oil based on Improved Verhulst Grey Theory［C］//2008 3rd IEEE Conference on Industrial Electronics and Applications，Singapore，2008:2042-2044.

7 LUO YOUXIN，CHEN MIANYUN，CHE XIAOYI，et al.Non-equal Interval Direct Optimizing Verhulst Model that x(n)be Taken as Initial Value and its Application［J］.Journal of Southeast University(English Edition)，2008，24(Sup):17-21.

8 左燕.基于GM(1，1)改進的Verhulst模型預測PTA期貨價格［J］.周口師范學院學報，2009，26(5):38-40.

9 何文章，吳愛弟.估計Verhulst模型中參數的線性規劃方法及應用［J］.系統工程理論與實踐，2006，26(8):141-144.

10 劉思峰，黨耀國，方志耕.灰色系統理論及其應用［M］.北京:科學出版社，2004.