π-H-模余代數的Morita-Takeuchi關系*
陳丹慧, 李金其, 張 濤
(1.浙江師范大學數理與信息工程學院,浙江金華 321004;2.武警上海政治學院數理教研室,上海200435)
0 引言
Morita定理在研究模和環的性質中有著很重要的地位.Takeuchi[1]給出了余模的Morita關系,故稱之為Morita-Takeuchi關系,簡稱為M-T關系,它為研究余模和余代數的性質提供了新的方法.
若H是域K上的co-Frobenius Hopf π-余代數,A是π-H-余模代數,文獻[2]建立了Smash積π-分次代A°之間的Morita關系.本文則研究了π-H-模余代數,得到了與之相對應的M-T關系.
本文的討論都在域 K上進行,為完整起見,先給出一些基本概念[1,3-4].為方便,文中省略和號“∑”.
設C是余代數,(M,ρM)是右C-余模,(N,ρN)是左 C-余模,余張量積 M□CN 是指 ρM?idN-idM?ρN:M?N→M?C?N的核,即 M□CN=ker(ρM?idN-idM?ρN).
定義 1[3]Hopf π-余代數 H=({Hα,mα,1α},Δ,ε,S)指的是 π-余代數 H=({Hα},Δ,ε)及一族線性映射 S={Sα:Hα→Hα-1}α∈π(稱為 H 的對極)滿足:
1)對任意的 α∈π,(Hα,mα,1α)為代數;
2)對任意的 α,β∈π,Δαβ:Hαβ→Hα?Hβ及 ε:H1→K 為代數同態;
3)對任意的 α∈π,mα(Sα-1?idα)Δα-1,α= ε1α=mα(idα?Sα-1)Δα,α-1.
顯然,(H1,m1,11,Δ1,1,ε,S1)是 Hopf代數.
若對任意的α∈π,Hα都是有限維的,則稱Hopf π-余代數H是有限型的;若每個Sα都是雙射,則稱對極 S={Sα}α∈π是雙射.
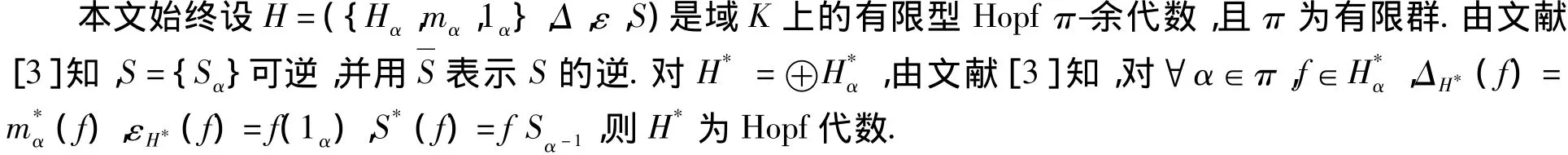
1 π-H-模余代數
定義2 設H是Hopf π-余代數,C是余代數.若對任意的α∈π,C是Hα-模,且對任意的α,β∈π,c∈C,hαβ∈Hαβ,l∈H1,滿足 Δ(hαβ·c)=h(1,α)·c1?h(2,β)·c2,ε(l·c)= εH(l)εC(c),則稱 C 為左 π-H-模余代數.
由文獻[3]知,設 H 是 Hopf π-余代數,V 是線性空間.若對任意的 α,β∈π,ρVα:V→V?Hα滿足
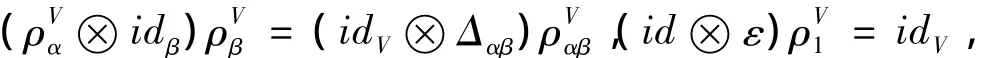
則稱(V,{ρVα}α∈π)是右 π-H-余模.
定義 3 設 H 是 Hopf π-余代數,C 是余代數,且(C,{ρCα}α∈π)是右 π-H-余模.若對任意的 α∈π,滿
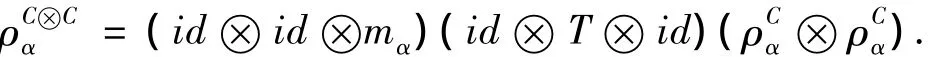
定義4 設 C 是左 π-H-模余代數.若對任意的 α∈π,φα:C→Hα是 Hα-模同態,則稱 φ ={φα}α∈π為C的π-余積分.
定理1 設C是左π-H-模余代數.若存在π-余積分 φ={φα}α∈π,且對任意的 α,β∈π滿足
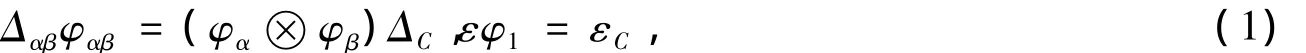
證明 對任意的c∈C,有:
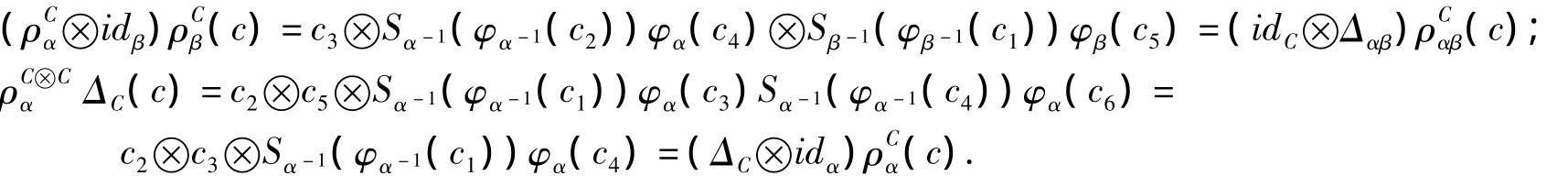
定理2 設C是左π-H-模余代數.若存在π-余積分φ={φα}α∈π,且對任意的α,β∈π滿足式(1),則 C ×H=({C?Hα}α∈π,Δ ={Δαβ},ε)為 π-余代數,稱之為 π-Smash 余積.其中,對任意的 c∈π,h∈
證明 對任意的 α,β,γ∈π,有
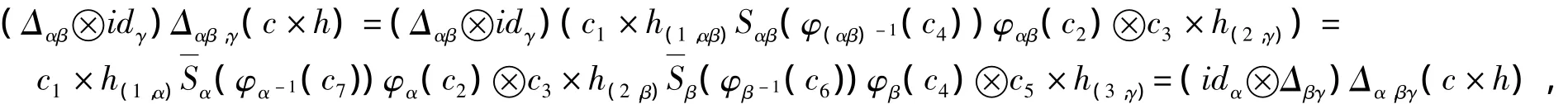
易證(idα?ε)Δα,1=(ε?idα)Δ1,α=id.所以,C × H 為 π-余代數.
2 Morita-Takeuchi關系

引理2 設C是左π-H-模余代數.若存在π-余積分φ={φα}α∈π,且對任意的α,β∈π滿足式(1),則C有誘導的左和右的π-C×H-余模結構,其中對任意的α∈π,c∈ C,定義
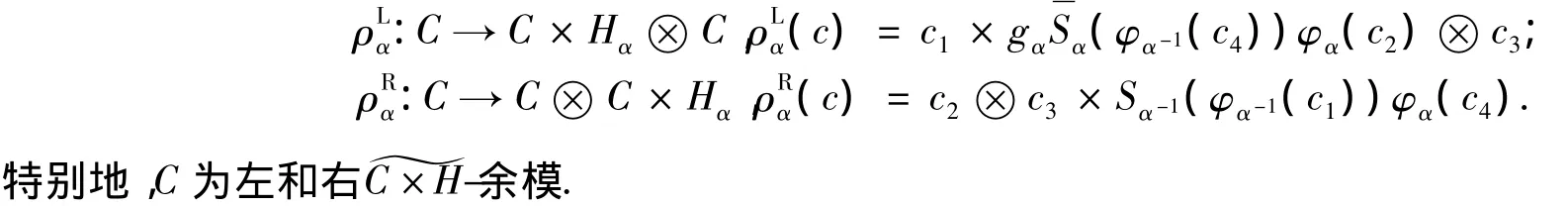
證明 對任意的α,β∈π,c∈C,有:
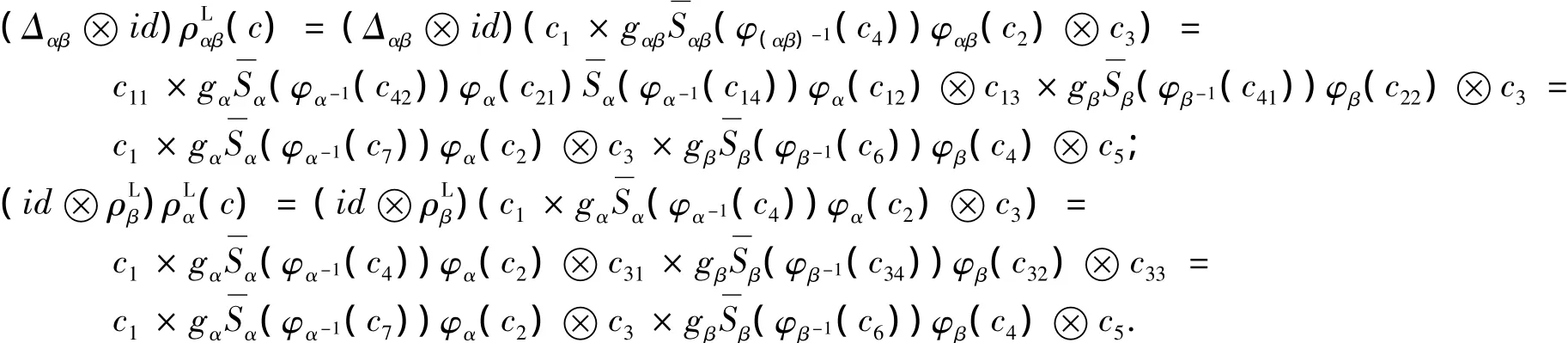

證明 由引理3的1)及式(2)和式(4)知,對任意的α∈π,有
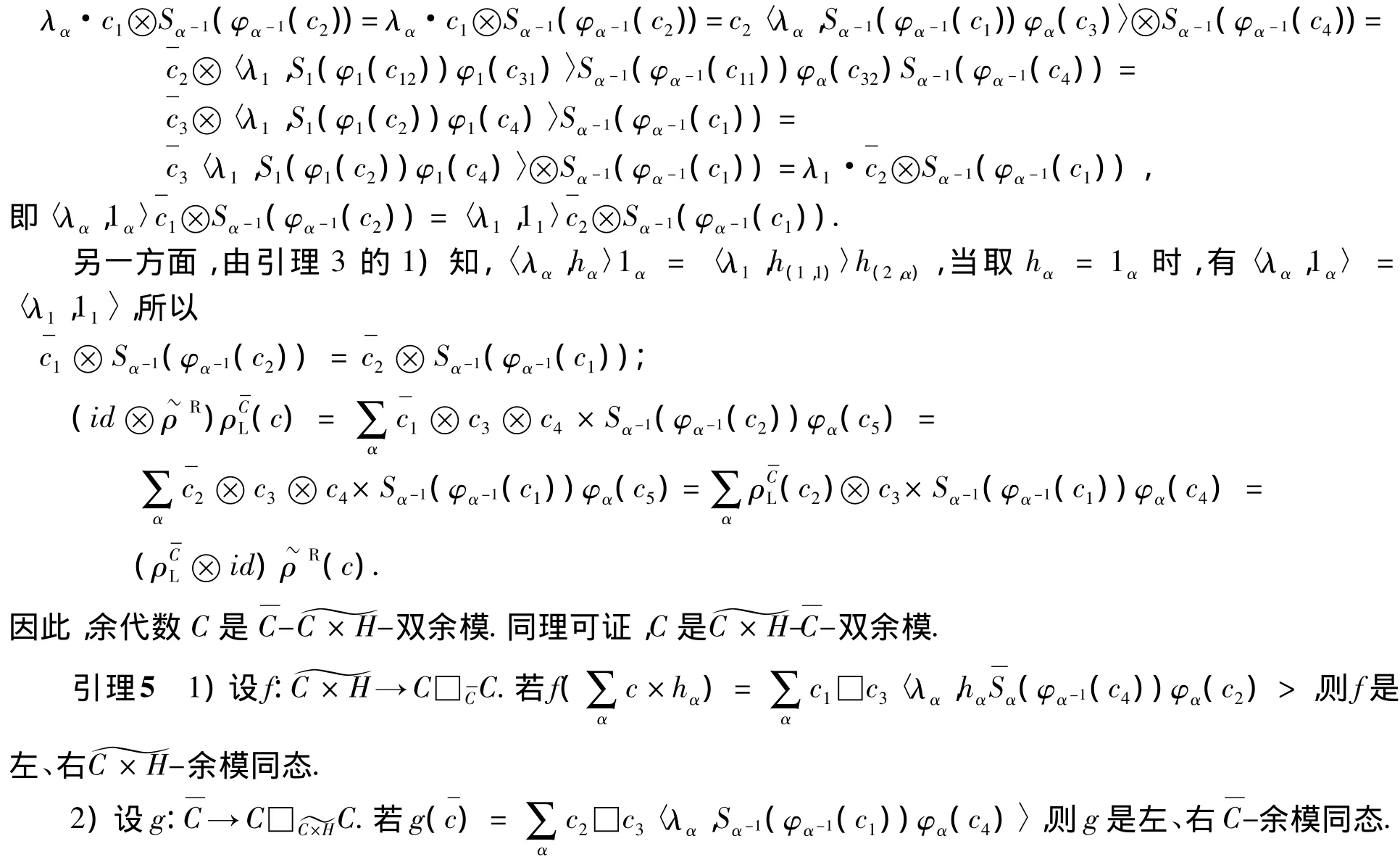
證明 1)先證明f的定義是合理的(其中記Δ(λα)=λα(1)?λα(2)).由于

故Im G?C□?C×HC.另一方面,由于
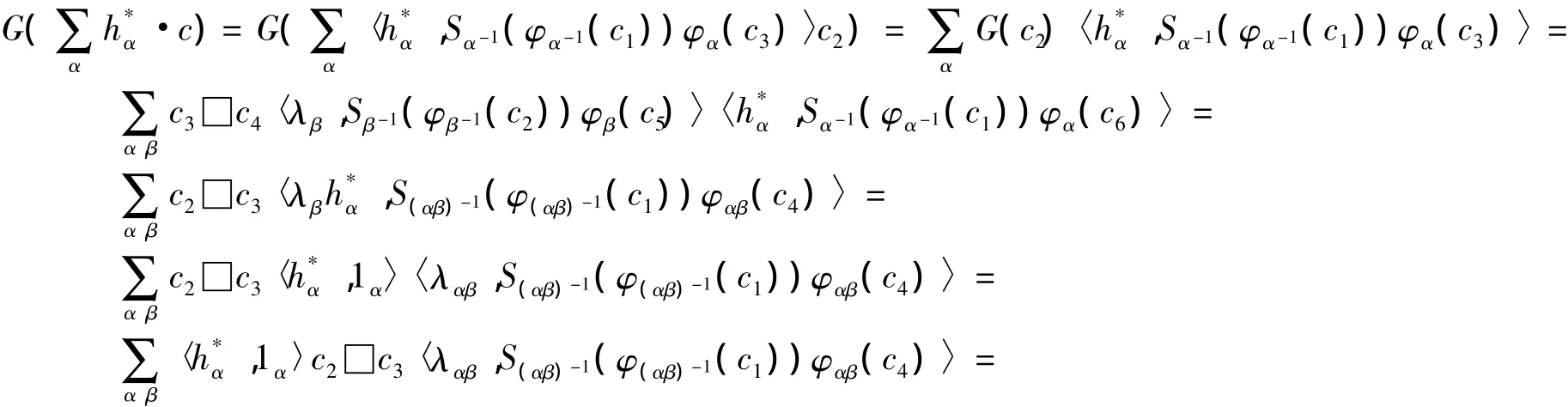

有了以上的準備工作,可得到定理3.

[1]Takeuchi M.Morita theorems for categories of comodules[J].J Fuc Sci Univ Tokyo Sect 1A Math,1977,24(3):629-644.
[2]Wang Shuanghong.Morita contexts,π-galois extension for Hopf π-coalgebras[J].Comm Algebra,2006,34(2):521-546.
[3]Virelizier A.Hopf group-coalgebras[J].J Pure Appl Algebra,2002,171(1):75-122.
[4]Sweedler M E.Hopf algebra[M].New York:Benjamin,1969.

