條形納米通道中奇特的鈉選擇性*

吳林松， 吳鋒民， 陸杭軍， 何俊霞， 聶雪川， 寇建龍

(浙江師范大學凝聚態物理研究所，浙江金華 321004)

0 引言

納米孔道的離子選擇性一直受到廣泛關注［1-7］，主要是因為:在生物體系中存在許多具有離子選擇性的孔道(離子通道)，這些離子通道與很多重要的生命活動過程有關，而其選擇機制還沒有完全被理解．早期研究是假定在K+通道結構固定不變的條件下，認為通道中的羰基構成的水合殼層很適合K+，而對Na+來說距離太遠，不能形成Na+的水合層，因此對Na+來說很不適合，所以K+比Na+的通透率大［8］．但是這個假設并不合理，因為這種管壁具有一定程度的柔性，必須考慮熱擾動，其殘基振動幅度可以達到約0．07 nm［4］．現在，有研究認為K+通道的選擇性主要是由于羰基配體之間的排斥力所引起的．最近，有研究人員［9］模仿Na+通道，通過在碳納米管上修飾羰基((9，9)型納米管)，分別實現了K+和Na+的選擇．研究發現:米管內存在著一定的離子選擇性;同時，離子的選擇性行為被認為是與納米管本身的幾何限制結構和離子的第1殼層配體有關［10-16］．另外也有科學家［17］運用帶電的管道實現了多種離子的選擇．盡管離子分離技術已經有了一定的發展，但是仍然有很多難題需要攻克．例如:K+和Na+2種單價離子的分離;如何在保證選擇性的前提下提高通透效率等等，這些問題是設計過濾膜的關鍵基礎問題．本文通過對石墨面構成的條形納米通道的離子選擇性行為的研究來探討納米孔道的離子選擇機制，同時希望設計出具有離子選擇性并有高通透效率的納米通道．條形納米通道相對于碳納米管來說離子在通道中的束縛明顯減少，但是研究表明它的選擇性行為并未出現消退．因此，這種孔道可以讓離子的輸運速率大大加快．這種納米通道構成的膜在離子分離與海水淡化中具有更大的優勢．

1 計算方法和模型

模擬系統如圖1所示．圖1中條形納米通道由上下2塊長為2．11 nm、寬為4．97 nm的單層石墨片構建而成，中間的條形納米通道由2塊長為2．11 nm，寬為4．97 nm的單層石墨片構成，嵌在由2塊石墨片構成的膜中，膜兩邊為離子溶液．定義2塊石墨片之間的距離為d．本文模擬了4種不同寬度(即不同d值)的條形納米通道的離子選擇性，d分別為:0．88，0．90，0．95，1．00 nm．模擬水盒子大小設定為:Lx=6．00 nm，Ly=5．11 nm，Lz=5．00 nm．把條形納米通道沿x方向嵌入由石墨片構成的膜中，膜把水盒子分成左右2部分．其兩側充滿水分子，水分子采用tip3p［18］模型，水中共加入 30 個 Na+，30 個 K+，60 個 Cl－，構成離子溶液(KCl和 NaCl的濃度約為0．46 mol/L)．沿條形納米通道方向施加0．01 V/nm的電場，其大小與生物系統中的電場相接近．

本文采用分子動力學軟件GROMACS 4．0．7［19］進行模擬，采用GROMACS自帶的力場和NVT系綜，Berendsen控溫法，溫度設定為T=300 K．為了便于研究問題，在整個模擬過程中條形納米通道與膜固定不動．其碳原子的范德華參數為:εC-C=0．361 2 kJ/mol，σC-C=0．34 nm．為了減少計算量，短程相互作用勢能截斷半徑rc=1．0 nm．電相互作用采用PME算法［20］．本文所有模擬采用周期性邊界條件，時間步長為2 fs，每ps保存1次數據，模擬時間為305 ns，模擬數據分析從第6 ns開始．

圖1 模擬系統示意圖

2 結果與討論

當沿條形納米通道方向施加電場后，離子會在電場的作用下通過條形納米通道．分別對不同間距的條形納米通道的離子通透情況進行模擬研究，其結果如表1所示．表1表示的是后300 ns內陽離子(K+，Na+)沿著x方向的流動情況．其中ΔNa+和ΔK+分別表示Na+和K+在條形納米通道中朝+x方向通過的個數與朝－x方向通過的個數之差．表1最后一列(ΔNa+/ΔK+)則是2種離子的通過比率．從表1可以看出，除了d=1．00 nm的系統外，Na+比K+更容易通過條形納米通道，表現出明顯的鈉選擇性．特別是d=0．88 nm這個系統，Na+和K+的通過比率可達到6．當d逐漸增加時，2種陽離子的流量都會增大．同時，2種陽離子通過比率逐漸趨向于1，離子的選擇性逐漸減弱．

筆者分析了這4個系統中K+和Na+沿著x方向的概率密度分布(ρ)．下面是離子概率密度的計算方法:將條形納米通道沿著x方向(2．11 nm)分成1 000份，此時離子的概率密度可以通過下面的公式進行計算:

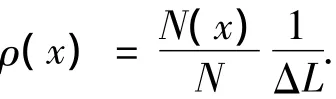
其中:ΔL表示1份的長度;N(x)是指模擬的N幀中在x位置所在的這份出現的離子總數．

2種離子的概率密度分布具體結果如圖2所示．由圖2可知，4種孔道中Na+的概率密度要高于K+的概率密度．換句話說，Na+更容易進入孔道．所以，這幾個系統都有一定的鈉選擇性．

表1 不同間距的條形納米通道的離子通透情況模擬結果

圖2 2種離子沿著x方向的離子概率密度分布示意圖

K+通道的K+/Na+通過比率高達1 000∶1，而鈉孔道的Na+/K+選擇比率也能達到500∶1．離子進入生物孔道中將脫去一定的配體數，而第1殼層配體數的變化對通道的選擇性有很大的影響．Na+和K+在宏觀水相中的第1殼層平均配體數分別為5．72和6．88個．Na+在宏觀水相中出現5個配體數的概率約為21%，6個配體數的概率約為69%．另外，K+在宏觀水相中配體數分布主要集中在6(約為30%)，7(約為41%)，8(約為 20%)．

K+和Na+在通道中的第1殼層配體數概率分布如圖3所示．從圖3容易得出d=0．88 nm的系統中，Na+的第1殼層配體數比K+更接近于宏觀水相中的分布．需要說明的是，一種離子在孔道中的配體數分布越接近宏觀水相中的分布，那么該孔道就越有利于這種離子通過．因此，筆者看到d=0．88 nm的系統中Na+比K+流通量大得多，形成了Na+選擇性．同時，從圖3中容易發現，隨著通道管徑的增大，2種離子的第1殼層配體數分布都會越來越接近于宏觀水相中的分布．換句話說，孔道的管徑增大，2種離子都會比較容易通過．從而得到當d=1．00 nm時孔道的選擇性幾乎消失．

進一步分析Na+和K+在條形納米通道內沿著x方向的第1殼層平均配體數概率分布，結果如圖4所示，bulk K+和 bulk Na+分別指宏觀水相中的第1殼層平均配體數．

由圖4 可知，d=0．88，0．90，0．95 nm 這 3 個系統的Na+第1殼層平均配體數分別約為:5．33，5．48，5．56．K+在這 3 個系統中的平均配體數分別約為5．63，5．98，6．47．而宏觀水相中Na+和K+的第1殼層平均配體數則分別為5．72和6．88．由這些結果可知，Na+相對于 K+來說更接近于它在宏觀水相中的分布．

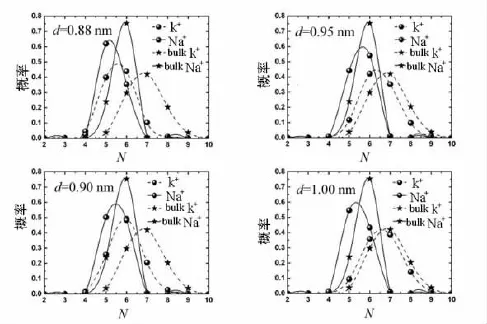
圖3 2種離子在4種管內和在宏觀水相中的第1殼層配體數概率分布示意圖

筆 者 發 現，d=0．88，0．90，0．95 nm 系統存在著Na+選擇性．而從 d=1．00 nm開始，發現K+和Na+的平均配體數分別為6．63和5．44，可以說都比較接近宏觀水相的配體數．因此該系統沒有出現離子選擇性．

圖4 Na+和K+沿著x方向的第1殼層平均配體數分布圖

為了更清楚地說明這幾種條形納米通道的選擇性，筆者同時探究了電場強度對孔道離子選擇性的影響．將選擇性最強的系統(d=0．88 nm)通過增大電場來觀察其鈉選擇性行為的變化，具體結果如圖5所示．

從圖5中容易發現，隨著電場強度的增大，條形孔道中的鈉選擇性行為在逐漸減弱．同時通透比率的變化并不是隨著電場增大而線性減小．引起通透比率減小的主要原因是由于電場強度增大，相應離子的驅動力就會增大，當驅動力增大到一定程度后，K+也變得很容易通過，因此，通透比率會逐漸減弱．

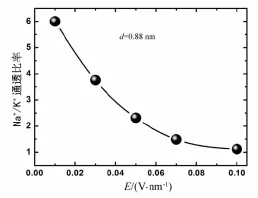
圖5 系統在不同電場條件下的通透比率分布

3 結論

通過分子動力學模擬，發現了條形納米通道中存在離子選擇性．而這種選擇機制主要是由于2種離子在通道內配體數與它們在宏觀水相中第1殼層的配體數分布不一樣引起的．另外，通過模擬發現，孔道的鈉選擇性會隨著外加電場的逐漸增大而減小．結果分析認為，這種條形納米通道具備一定的優勢:1)這種孔道相對來說更加簡單，也更容易讓人們修飾相應的殘基;2)d=0．88 nm系統只要施加E=0．01 V/nm的驅動就能驅動離子通過孔道，而且K+和Na+通過比率可以達到6．但是對于柱形無修飾的管道，要達到這個選擇比率非常困難，因為柱形納米通道中要存在這種選擇比率的孔道，其管徑非常小，需要極大的驅動力才可以讓離子通過孔道．因此，有理由相信條形納米通道的選擇性研究對未來離子分離的實驗和理論研究都會有幫助．

［1］Benèche S，Roux B．Energetics of ion conduction through the K+channel［J］．Nature，2001，414:73-77．

［2］Benèche S，Roux B．A microscopic view of ion conduction through the K+channel［J］．Proc Natl Acad Sci USA，2003，100:8644-8648．

［3］Noskov S Y，Roux B．Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels［J］．J Gen Physiol，2007，129:135-143．

［4］Noskov S Y，Berneche S，Roux B．Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands［J］．Nature，2004，431:830-834．

［5］Dudev T，Lim C．Determinants of K+vs Na+selectivity in potassium channels［J］．J Am Chem Soc，2009，131，8092-8101．

［6］Dudev T，Lim C．Effect of carboxylate-binding mode on metal binding/selectivity and function in proteins［J］．Acc Chem Res，2007，40:85-93．

［7］Thomas M，Jayatilaka D，Corry B．The predominant role of coordination number in potassium channel selectivity［J］．Biophys J，2007，93:2635-2643．

［8］Hille B，Armstrong C，MacKinnon R．Ion channels:From idea to reality［J］．Nat Med，1999，5:1105-1109．

［9］Gong X J，Li J C，Xu K，et al．A controllable molecular sieve for Na+and K+ions［J］．J Am Chem Soc，2010，132:1873-1877．

［10］Beckstein O，Tai K，Sansom M S P．Not ions alone:barriers to ion permeation in nanopores and channels［J］．J Am Chem Soc，2004，126，14694-14695．

［11］Bostick D L，Brooks Ⅲ C L．Selectivity in K+channels is due to topological control of the permeant ion's coordinated state［J］．Proc Natl Acad Sci USA，2007，104:9260-9265．

［12］Bostick D L，Arora K，Brooks Ⅲ C L．K+/Na+selectivity in toy cation binding site models is determined by the‘Host’［J］．Biophys J，2009，96:3887-3896．

［13］Song C，Corry B．Intrinsic ion selectivity of narrow hydrophobic pores［J］．J Phys Chem B，2009，113:7642-7649．

［14］Shao Q，Zhou J，Lu L H，et al．Anomalous hydration shell order of Na+and K+inside carbon nanotubes［J］．Nano Lett，2009，9:989-994．

［15］Joseph S，Mashl R J，Jakobsson E，et al．Electrolytic transport in modified carbon nanotubes［J］．Nano Lett，2003，3:1399-1403．

［16］Peter C，Hummer G．Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations［J］．Biophys J，2005，89:2222-2234．

［17］Sint K，Wang B Y，Kral P．Selective ion passage through functionalized graphene nanopores［J］．J Am Chem Soc，2008，130:16448-16449．

［18］Jorgensen W L，Chandrasekhar J，Madura J D，et al．Comparison of simple potential functions for simulating liquid water［J］．J Chem Phys，1983，79:926-935．

［19］Spoel D van der，Lindahl E，Hess B，et al．GROMACS:Fast，flexible，and free［J］．J Comp Chem，2005，26:1701-1718．

［20］Darden T，York D，Pedersen L．Particle mesh Ewald:An N．log(N)method for Ewald sums in large systems［J］．J Chem Phys，1993，98:10089-10092．