最大度為6且不含5-圈和相鄰4-圈的平面圖是7-全可染的*

張靜雯

(浙江師范大學(xué)數(shù)理與信息工程學(xué)院，浙江金華 321004)

0 引言

本文所研究的圖是有限簡(jiǎn)單無(wú)向圖，文中未加定義的術(shù)語(yǔ)和記號(hào)參閱文獻(xiàn)［1］．

如果圖G可嵌入到平面上，使得邊僅在端點(diǎn)處相交，則稱(chēng)圖G是可平面圖;可平面圖在平面內(nèi)的一個(gè)嵌入叫平面圖．對(duì)于平面圖G，分別用V，E，F(xiàn)，Δ和δ表示平面圖G的頂點(diǎn)集、邊集、面集、最大度和最小度．k-圈是指長(zhǎng)度為k的圈;兩個(gè)圈相鄰是指該兩個(gè)圈至少有1條公共邊．

設(shè)平面圖G=(V，E)，若映射 φ:V∪E→{1，2，…，k}，使得對(duì)任意相鄰或相關(guān)聯(lián)的元素 x，y∈V∪E都有φ(x)≠φ(y)，則稱(chēng)G是k-全可染的．顯然，給每一個(gè)圖進(jìn)行全染色至少要用Δ+1種顏色．文獻(xiàn)［2-3］猜想:任何簡(jiǎn)單圖G都是(Δ+2)-全可染的．這一猜想就是著名的全染色猜想(Total Coloring Conjecture)，簡(jiǎn)記為 TCC．

即使對(duì)于平面圖，TCC也未得到完整的證明．唯一未解決的困難情形是Δ=6．這方面的一些研究結(jié)果可參見(jiàn)文獻(xiàn)［4-8］．人們期望得到關(guān)于簡(jiǎn)單平面圖全染色的最好結(jié)果，即證明平面圖是(Δ+1)-全可染的．到目前為止，已經(jīng)證明了在大多數(shù)情況下，簡(jiǎn)單平面圖是(Δ+1)-全可染的．文獻(xiàn)［9-11］分別證明了Δ≥11，Δ=10和Δ=9的平面圖是(Δ+1)-全可染的;文獻(xiàn)［12］證明了Δ≥7且不含4-圈的簡(jiǎn)單平面圖是(Δ+1)-全可染的．本文研究的是關(guān)于Δ=6的平面圖的全染色問(wèn)題，得到如下結(jié)果:

定理1 設(shè)G是Δ=6且不含5-圈和相鄰4-圈的平面圖，則圖G是7-全可染的．

1 定理1的證明

假設(shè)定理1不成立，并設(shè)圖G是定理1的一個(gè)使σ(G)=|V|+|E|最小的反例，即Δ(G)=6且不含5-圈和相鄰4-圈，它本身不是7-全可染的，但它的每一個(gè)真子圖都是7-全可染的，則圖G有以下幾個(gè)性質(zhì):

斷言1［9］圖G是2-連通的．

δ≥2，且因?yàn)閳DG是2-連通的，所以G的每個(gè)面的邊界都是圈．

把度數(shù)為k的點(diǎn)叫做k-點(diǎn);類(lèi)似地，把度數(shù)至少為k的點(diǎn)叫做k+-點(diǎn);把度數(shù)至多為k的點(diǎn)叫做k--點(diǎn)．(i，j)-邊是指此邊的2個(gè)端點(diǎn)的度數(shù)分別為 i和 j;(i，j，k)-面是指此 3-面上的點(diǎn)的度數(shù)分別為 i，j，k．

斷言 2［13］設(shè) xy∈E．若 d(x)≤3，則d(x)+d(y)≥Δ +2=8．

特別地，G中2-點(diǎn)只與6-點(diǎn)相鄰，3-點(diǎn)只與5+-點(diǎn)相鄰．

斷言3［13］圖G中所有(2，6)-邊的導(dǎo)出子圖是一個(gè)森林．

斷言4 G不含圖1所示的結(jié)構(gòu)．其中標(biāo)記為·的點(diǎn)在G中沒(méi)有其他鄰點(diǎn)．

證明 假設(shè)G有如圖1(a)所示的子結(jié)構(gòu)．由G的極小性可知，G'=G-u1u3是7-全可染的．假設(shè)φ是G'的一個(gè)7-全染色，抹去u1和u4的色，則得到圖G的一個(gè)部分全染色，其中未染的元素是u1u3，u1和u4．易見(jiàn)，當(dāng)u1u3染好后，u1和u4的色可重染好．所以，以下只需看u1u3是否可染好．S(u)表示在φ

圖1 可約構(gòu)型

若7∈{φ(u4u5)，φ(u5u6)}，則當(dāng) φ(u4u5)=7時(shí)，如果 φ(u5u6)≠φ(u3u4)，那么交換 u3u4與 u4u5的色，再將φ(u3u4)染給u2u3;如果φ(u5u6)=φ(u3u4)，那么交換u1u2與u1u3的色，再將φ(u1u3)染給u3u5，φ(u3u5)染給 u2u3;當(dāng) φ(u5u6)=7 時(shí)，則交換 u1u2與 u1u3的色，如果 φ(u4u5)≠φ(u1u3)，那么再將 φ(u1u3)染給 u3u5，φ(u3u5)染給 u2u3;如果 φ(u4u5)=φ(u1u3)，那么交換 u3u4與 u4u5的色，再將φ(u3u4)染給u2u3;最后，重染u2和u5，又得G是7-全可染的，矛盾．

假設(shè)G有如圖1(c)所示的子結(jié)構(gòu)．由G的極小性可知，G'=G-u2u3是7-全可染的．假設(shè)φ是G'的一個(gè)7-全染色，抹去u2和u5的色，則得到圖G的一個(gè)部分全染色，其中未染的元素是u2u3，u2和u5．

若|S(u2)∪S(u3)|≤6，則u2u3可染;再重染u2和u5，則G是7-全可染的，矛盾．

若|S(u2)∪S(u3)|=7，不妨設(shè)S(u3)={1，2，…，5}，S(u2)={6，7}，則可斷言{φ(u4u5)，φ(u5u6)}={6，7}．否則，若 6?{φ(u4u5)，φ(u5u6)}，則可將 φ(u3u5)染為 6，φ(u3u5)染給 u2u3;同理可證，7∈{φ(u4u5)，φ(u5u6)}．此時(shí)交換u3u4與u4u5的色，再將 φ(u3u4)染給 u2u3;最后，重染 u2和 u5，又得 G是7-全可染的，矛盾．?dāng)嘌?證畢．

2 權(quán)轉(zhuǎn)移

以下將運(yùn)用Discharging方法導(dǎo)出矛盾，完成定理1的證明．首先，給圖G的每個(gè)頂點(diǎn)v分配初始權(quán)

以下將定義一個(gè)權(quán)轉(zhuǎn)移規(guī)則，重新分配點(diǎn)和面的權(quán)，設(shè)ch'(x)是重新分配點(diǎn)和面的權(quán)后元素x∈只是在同一個(gè)圖的點(diǎn)和面之間進(jìn)行權(quán)轉(zhuǎn)移，則權(quán)的總和應(yīng)保持不變，所以得出 -12≥0的矛盾，完成定理1的證明．

權(quán)轉(zhuǎn)移規(guī)則如圖2所示．

圖2 權(quán)轉(zhuǎn)移規(guī)則

R1:轉(zhuǎn)向2-點(diǎn)的權(quán)

與2-點(diǎn)相鄰的2個(gè)6-點(diǎn)都向2-點(diǎn)轉(zhuǎn)移權(quán)1．

R2:轉(zhuǎn)向3-面的權(quán)

R2．1:若3-面與3--點(diǎn)相關(guān)聯(lián)，則3-面上的2個(gè)5+-點(diǎn)都向3-面轉(zhuǎn)移

R2．2:若3-面不與3--點(diǎn)相關(guān)聯(lián)，則3-面上的3個(gè)4+-點(diǎn)都向3-面轉(zhuǎn)移權(quán)1．

R3:轉(zhuǎn)向4-面的權(quán)

R3．1:若4-面與2個(gè)3--點(diǎn)相關(guān)聯(lián)，則4-面上的2個(gè)5+-點(diǎn)都向4-面轉(zhuǎn)移權(quán)1;

R3．2:若4-面與1個(gè)3--點(diǎn)相關(guān)聯(lián)，則與3--點(diǎn)相鄰的2個(gè)5+-點(diǎn)都向4-面轉(zhuǎn)移的4+-點(diǎn)向4-面轉(zhuǎn)

R3．3:若4-面不與3--點(diǎn)相關(guān)聯(lián)，則4-面上的4個(gè)4+-點(diǎn)都向4-面轉(zhuǎn)

首先考察面的新權(quán)．

設(shè) f為 3-面．若 f與 3--點(diǎn)相關(guān)聯(lián)，則根據(jù) R則根據(jù) R2．2，ch'(f)≥ch(f)+1 ×3=0．

設(shè) f為4-面．若 f與2 個(gè)3--點(diǎn)相關(guān)聯(lián)，則根據(jù) R3．1，ch'(f)≥ch(f)+1 ×2=0;若 f與1 個(gè)3--點(diǎn)相

由圖G不含5-圈知圖G不含5-面，故無(wú)需驗(yàn)證5-面的新權(quán)．

設(shè)f為6+-面．由權(quán)轉(zhuǎn)移規(guī)則知f既不轉(zhuǎn)出權(quán)也不接受權(quán)，因此ch'(f)=ch(f)=d(f)-6≥0．

綜上所述，對(duì)任意的面f∈F，ch'(f)≥0．

其次考察頂點(diǎn)的新權(quán)．

設(shè)v為2-點(diǎn)．由斷言2和R1知，ch'(v)=ch(v)+1×2=-2+2=0．

設(shè)v為3-點(diǎn)．由權(quán)轉(zhuǎn)移規(guī)則知v既不轉(zhuǎn)出權(quán)也不接受權(quán)，即ch'(v)=ch(v)=0．

下面用t表示與v相關(guān)聯(lián)的3-面的個(gè)數(shù)．

的4-面，轉(zhuǎn)移權(quán)1給與它相鄰的2-點(diǎn)．

用n表示與v相鄰的2-點(diǎn)個(gè)數(shù)，顯然，n≤6．與6-點(diǎn)相鄰的2-點(diǎn)分布情況如圖3所示．以下分2種情形討論:

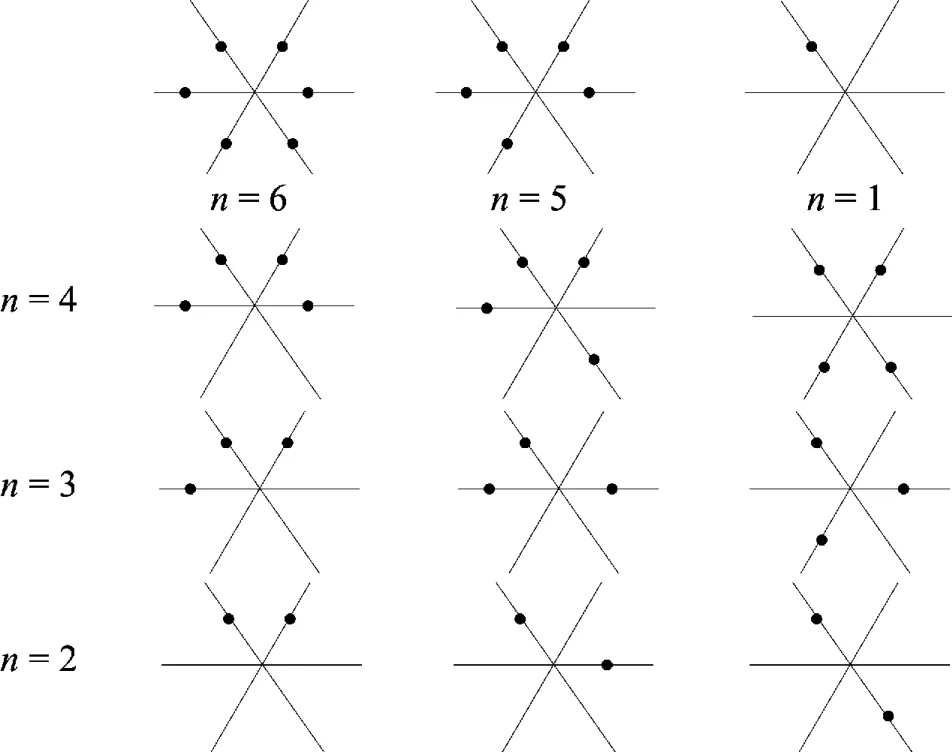
圖3 與6-點(diǎn)相鄰的2-點(diǎn)分布情況(1≤n≤6)

最復(fù)雜的為t=0．用m表示與v相關(guān)聯(lián)的4-面?zhèn)€數(shù)，由圖G不含5-圈和相鄰4-圈知m≤3．

注2 由斷言3和圖G不含5-圈知，與v關(guān)聯(lián)且關(guān)聯(lián)的2個(gè)與v相鄰的2-點(diǎn)的面是6+-面．

n=6．由注1和注2知，ch'(v)≥ch(v)-1×6=0．

n=5．由注2和圖 G不含相鄰4-圈知 v至少關(guān)聯(lián)5個(gè)6+-面，且 m≤1，從而根據(jù)注1，ch'(v)≥ch(v)-1×5-1=0．

n=4．由注2和圖G不含相鄰4-圈知m≤2，從而根據(jù)注1，ch'(v)≥ch(v)-1×4-1×2=0．

n=3．由注2和圖G不含相鄰4-圈知m≤3，從而根據(jù)注1，ch'(v)≥ch(v)-1×3-1×3=0．

n=2．由注2和圖G不含相鄰4-圈知m≤3，從而根據(jù)注1，ch'(v)≥ch(v)-1×2-1×3≥0．

n=1．由圖G不含相鄰4-圈知m≤3，從而根據(jù)注1，ch'(v)≥ch(v)-1-1×3≥0．

至此，對(duì)任意的x∈V∪F，ch'(x)≥0已得到驗(yàn)證．定理1得證．

［1］Bondy J A，Murty U S R．Graph theory with applications［M］．London:Macmillan Press，1976．

［2］Vizing V G．Some unsolved problems in graph theory［J］．Uspekhi Mat Nauk，1968，23(6):117-134．

［3］Behzad M．Graphs and their chromatic numbers［D］．East Lansing:Michigan State University，1965．

［4］Kostochka A V．The total coloring of a multigraph with maximal degree 4［J］．Discrete Math，1977，17(2):161-163．

［5］Kostochka A V．The total chromatic number of any multigraph with maximal degree five is at most seven［J］．Discrete Math，1996，162(1/2/3):199-214．

［6］Rosenfeld M．On the total coloring of certain graphs［J］．Israel J Math，1971，9(3):396-402．

［7］Vijayaditya N．On total chromatic number of a graph［J］．London Math Soc，1971，3(2):405-408．

［8］Yap H P．Total coloring of graphs［M］．Belin:Spring-Verlag，1996．

［9］Borodin O V，Kostochka A V，Woodall D R．Total coloring of planar graphs with large maximum degree［J］．Graph Theory，1997，26(1):53-59．

［10］Wang Weifan．Total chromatic number of planar graphs with maximum degree ten［J］．Graph Theory，2007，54(1):91-102．

［11］Kowalik L，Sereni J S，?krekovski R．Total coloring of plane graphs with maximum degree nine［J］．SIAM Discrete Math，2008，22(4):1462-1479．

［12］Hou Jianfeng，Liu Guizhen，Cai Jiansheng．List edge and list total coloring of planar graphs without 4-cycles［J］．Theoret Comput Sci，2006，369:250-255．

［13］Borodin O V．On the total coloring of planar graphs［J］．Reine Angew Math，1989，394(1):180-185．