基于斷裂力學及隨機有限元的隧道巖爆風險分析

趙延喜，李 浩

基于斷裂力學及隨機有限元的隧道巖爆風險分析

趙延喜，李 浩

（江蘇省交通規劃設計院有限公司，南京 210005）

國內外大多數的巖爆預測方法中，都是利用應力強度比進行巖爆預測，該理論未考慮工程中存在的大量不確定性。基于此，提出了巖爆發生的斷裂力學模型，即認為巖爆是由平行于自由表面的裂紋擴展造成的，在外荷載作用下，這些微小張性裂紋發生斷裂，逐漸擴展、相互連接，當達到一定程度后，形成一定形狀的肉眼可見的宏觀裂紋，最終導致巖石破壞。以巖爆的層裂板模型為基礎，運用可靠度原理及隨機有限元方法，建立了巖爆發生的概率風險模型。工程實例計算表明，基于斷裂力學及隨機有限元的巖爆分析模型，可以較好地反映工程實際，為類似工程提供參考。

巖爆；深埋隧道；斷裂力學；隨機有限元

在隧道開挖過程中，巖爆是常見的一種圍巖破壞形式。一般認為圍巖切向應力σθ達到或接近巖石單軸抗壓強度σc時發生巖爆，但巖爆的工程實錄表明，大多數巖爆發生時σθ小于σc。從國內外的巖爆預測方法［1－7］來看，所采用的巖爆分級指標也都是σθ遠小于σc，因此需重新對巖爆機理進行分析，基于此提出了巖爆機理的斷裂力學模型。由于工程中存在大量不確定性，現有巖爆預測模型并未考慮參數的隨機性，由此結合可靠度及隨機有限元方法，建立了巖爆預測的概率風險模型。

1 巖爆發生的斷裂力學分析

實際上圍巖中存在許多微小張性裂紋，在外荷載作用下，這些微小張性裂紋發生斷裂，并且逐漸擴展、相互連接。當達到一定程度后，會形成一定形狀的肉眼可見的宏觀裂紋，最終導致巖石破壞。如果積聚的能量較大，則會以彈射的方式出現，就是巖爆。巖爆典型的力學模型為層裂板模型，該模型由Dyskin等［8］提出，層裂板模型認為巖爆是由平行于自由表面的微裂紋擴展造成的，圖1為巖爆破壞發生過程。基于斷裂力學原理，提出了巖爆發生的斷裂力學模型，從巖爆實錄及現有巖爆判據來看是比較合理的。

圖1 巖爆破壞過程示意圖［8］Fig.1 The process of rockburst

實際上巖體內存在初始裂紋，如圖1（a）；隨著荷載增加，洞壁圍巖處各裂紋開始擴展；當裂紋滿足開裂條件，應力強度因子大于斷裂韌度時，即KI≥KIC時，翼裂紋將沿最大壓應力方向比較穩定地開始擴展，如圖1（b）；隨著荷載的繼續增大，由于裂紋間的相互作用，翼裂紋的擴展將不再穩定，裂紋發生相互連接而形成更長的裂紋，如圖1（c）；當裂紋繼續失穩擴展并且相互連接，最后會形成一個比較長的薄片狀巖層，在高地應力下，會出現較劇烈的巖爆現象，如圖1（d）。這一過程即為基于層裂板模型的巖爆發生機理。根據巖爆發生的層裂板模型，可以看出，最后形成的薄片狀巖層符合薄板的受力特點，因此采用彈性力學中的薄板壓曲原理分析，層裂板受壓模型見圖2。設圖2中的板為四邊簡支，在x＝0，x＝l的兩邊上，作用有均布壓力Px。本研究允許板各邊在平面內自由移動，則x方向上變形時不產生其它方向上的內力，即 Nx＝－Px，Ny＝Pxy＝0。

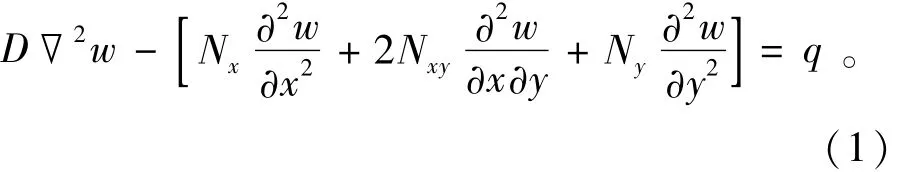
圖2 層裂板受壓模型［9］Fig.2 Lamination spallation buckling model

推導得出發生巖爆的臨界應力為

對于寬板，b?l，化簡后可得

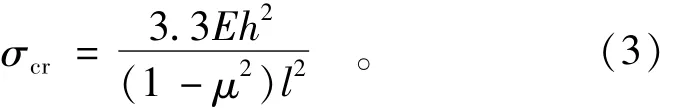
式中：E為彈性模量；h為薄板厚度；l為板長；b為板寬度；μ為泊松比。

對于深埋隧洞，當圍巖臨界應力≥σcr，隧洞圍巖就會由于宏觀斷裂，發生巖爆破壞。

2 巖爆風險功能函數模型

巖爆判別模型較多，但Russenes［10］根據洞室周邊最大切向應力與單軸抗壓強度比值提出的巖爆判別法最具實用價值，見表1。

將σθmax，σc視為隨機變量，則可以建立各等級巖爆的發生概率。

無巖爆：

表1 Russenes巖爆判別準則Table 1 Russenes criterion of identifying rockburst

弱巖爆：

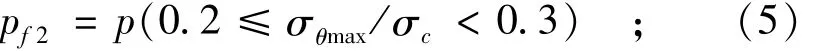
中巖爆：

強巖爆：

以上4式中，σθmax由隨機有限元方法求出，σc依據公式（3）求得。

3 工程實例

以某深埋隧洞為對象，建立數值模型。由于理論解往往難以準確計算洞室周邊最大水平應力，目前大部分用的都是確定性方法，基于隨機有限元方法比較少。因此采用概率設計技術進行基于有限元的概率分析，將輸入參數設為隨機變量，則可得到隧洞周邊最大切向應力σθmax，利用蒙特卡洛方法進行模擬，可得到各等級巖爆發生概率。

3.1 數值模擬參數

本計算以圍巖中存在最多的砂巖為研究對象，采用的隨機參數見表2。

3.2 數值模型的建立

由于本次模擬隧洞埋深不等，最大埋深達1 100 m。為了充分考慮開挖對隧洞圍巖的影響，取以隧洞軸線為中心的5倍開挖直徑范圍內的圍巖體作為模擬對象。同時，為了便于計算分析，將該問題按平面應變問題處理，在隧洞軸線方向上取單位長度，模型尺寸為60 m×60 m，隧洞半徑為5 m，如圖3所示。初始應力場只考慮垂直應力和水平應力，以水平應力為主。邊界條件假定模型左側邊界不發生側向位移，可沿豎直方向發生移動，下側底面邊界設計為不發生豎向位移，但可產生側向移動。破壞準則采用Drucker-Prager準則。

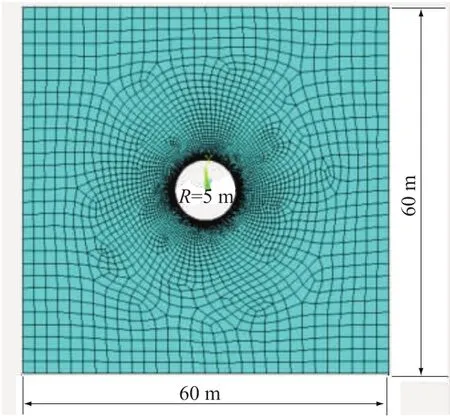
圖3 計算模型Fig.3 Computation model

3.3 計算結果分析

利用二維隨機有限元概率設計技術模擬3 000次，得圍巖最大切向應力，其均值和方差見圖4、圖5。

圖4 最大切向應力均值趨勢圖Fig.4 Tendency of the mean value of maximum tangential stress

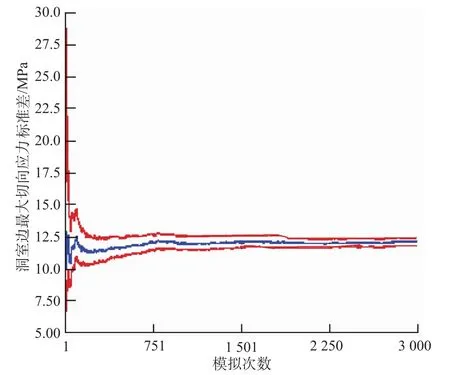
圖5 最大切向應力標準差趨勢圖Fig.5 Tendency of the standard deviation of maximum tangential stress

隧洞周邊最大切向應力近似服從正態分布，其均值為－55 MPa，為壓應力，標準差為12 MPa。根據前面建立的概率模型，依據隨機有限元程序計算得到的洞室周邊最大切向應力均值、最大切向應力標準差，采用monte-carlo方法模擬各等級巖爆的發生概率。參考挪威Russenes判別準則，設σθ服從正態分布，均值和標準差取二維隨機有限元PDS模擬結果分別為55 MPa和12 MPa；服從正態分布，均值和標準差分布為80 MPa和10 MPa。

采用蒙特卡羅法模擬10 000次，則可得應力強度比σθmax／σc的分布直方圖、超越概率分布曲線見圖6、圖7所示。

圖6 應力強度比分布直方圖Fig.6 Histogram of stress strength ratio

圖7 應力強度比超越概率曲線Fig.7 Exceedance probability versus stress strength ratio

由直方圖6可以看出，應力強度比均值為σθmax／σc＝0.554，則根據Russenes判別準則，發生強巖爆。根據圖7可以計算應力強度比大于任何值的概率，如Russenes準則，應力強度比大于0.2時發生巖爆，計算出發生巖爆的概率為99%。則各等級巖爆的發生概率分別如下。

無巖爆概率：pf1＝0.1%；

弱巖爆概率：pf2＝2.2%；

中巖爆概率：pf3＝48.04；

強巖爆概率：pf4＝49.66%。

由超越概率及累積概率分布，可見隧洞強度應力比小于0.2的概率為0.1%，幾乎為零，說明模擬位置肯定會發生巖爆。弱巖爆發生概率為2.2%，中等巖爆發生概率為48.04%，強巖爆發生概率為49.66%，則巖爆傾向于中－強巖爆，中等巖爆與強巖爆發生概率基本相等，由于本工程砂巖強度不是太高，加之巖體內部存在微裂隙，彈性應變能儲存不會太高，不太可能發生彈射型巖爆，而會發生類似于剝落的巖爆。

4 結 論

（1）由于巖爆發生并非都符合 Mohr-Coulomb準則，本文中采用斷裂力學分析巖爆發生機理，提出了巖爆發生斷裂力學模型。

（2）結合風險分析理論及隨機有限元技術，建立了巖爆風險概率模型，該模型能夠計算各等級巖爆發生概率，比確定性巖爆判別模型更加精確。

（3）工程實例計算表明，基于斷裂力學及隨機有限元的巖爆分析模型可以較好地反映工程實際，為類似工程提供了參考。

［1］ 徐林生，王蘭生.二郎山公路隧道巖爆發生規律與巖爆預測研究［J］.巖土工程學報，1999，21（5）：569－572.（XU Lin-sheng，WANG Lan-sheng.Study on the Laws of Rockburst and Its Forecasting in the Tunnel of Erlang Mountain Road［J］.Chinese Journal of Geotechnical Engineering，1999，21（5）：569－572.（in Chinese））

［2］ 劉章軍，袁秋平，李建林.模糊概率模型在巖爆烈度分級預測中的應用［J］.巖石力學與工程學報，2008，27（增 1）：3095－3103.（LIU Zhang-jun，YUAN Qiu-ping，LI Jian-lin.Application of Fuzzy Probability Model to Prediction of Classification of Rockburst Intensity［J］.Chinese Journal of Rock Mechanics and Engineering，2008，27（S1）：3095－3103.（in Chinese））

［3］ 呂 慶，孫紅月，尚岳全，等.深埋特長公路隧道巖爆預測綜合研究［J］.巖石力學與工程學報，2005，24（16）：2982－2988.（LV Qing，SUN Hong-yue，SHANG Yue-quan，et al.Comprehensive Study on Prediction of Rockburst in Deep and Over-Length Highway Tunnel［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（16）：2982－2988.（in Chinese））

［4］ 趙延喜，徐衛亞.基于模糊概率的深埋隧洞巖爆風險分析［J］.長江科學院院報，2008，25（6）：82－85.（ZHAO Yan-xi，XU Wei-ya.Risk Analysis of Rockburst in Deep-Buried Tunnels Based on Fuzzy Probability［J］.Journal of Yangtze River Scientific Research Institute，2008，25（6）：82－85.（in Chinese））

［5］ SHARAN SK.A Finite Element Perturbation Method for the Prediction of Rockburst［J］.Computers and Structures，2007，85（5）：1304－1309.

［6］ JIA P，TANG C A.Numerical Study on Failure Mechanism of Tunnel in Jointed Rock Mass［J］.Tunnelling and Underground Space Technology，2008，23（5）：500－507.

［7］ 宮鳳強，李夕兵.巖爆發生和烈度分級預測的距離判別方法及應用［J］.巖石力學與工程學報，2007，26（5）：1012－1018.（GONG Feng-qiang，LI Xi-bing.A Distance Discriminant Analysis Method for Prediction of Possibility and Classification of Rockburst and Its Application［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（5）：1012－1018.（in Chinese））

［8］ DYSKIN A V，ADHIKARY D P.A Cosserat Continuum Model for Layered Materials［J］.Computers and Geomechanics，1997，20（1）：15－45.

［9］ 馮 濤，潘長良.洞室巖爆機理的層裂屈曲模型［J］.中國有色金屬學報，2000，10（2）：287－290.（FENG Tao，PAN Chang-liang.Lamination Spallation Buckling Model for Formation Mechanism of Rockburst［J］.The Chinese Journal of Non-ferrous Metals，2000，10（2）：287－290.（in Chinese））

［10］陶振宇.高地應力區的巖爆及其判別［J］.人民長江，1987，20（5）：25－32.（TAO Zhen-yu.Rockburst at Insitu Stress Zone in Highland and Its Discrimination［J］.Yangtze River，1987，20（5）：25－32.（in Chinese） ）

Risk Analysis for Tunnel Rockburst Based on Fracture Mechanics and Stochastic FEM

ZHAO Yan-xi，LI Hao
（Jiangsu Provincial Communication Planning and Designing Institute Co.，Ltd.，Nanjing 210005，China）

Stress-strength ratio model is usually applied to rockburst prediction in China and abroad，but uncertainties in engineering are not taken into account in this method.A fracture mechanics model of rockburst mechanism is proposed in this paper.This model is based on the assumption that rockburst is caused by microcracks which parallel to the free surface.These microcracks will fracture，extend，and mutually connect under external load.Then visible macroscopic crack is formed and finally rockburst happens.Furthermore，a rockburst risk probability model is proposed using reliability theory and stochastic FEM method based on Lamination spallation buckling model.The model was applied to engineering project calculation and the result manifested its rationality.

rockburst；deep-buried tunnel；fracture mechanics；stochastic finite element method

U458.3

A

1001－5485（2011）06－0059－04

2010-08-14；

2011-01-04

國家自然科學基金項目（50909038）；國家科技支撐計劃項目（2006BAB04A06）

趙延喜（1980-），男，河南南陽人，博士，工程師，主要從事隧道設計與分析方面的研究工作，（電話）13739195910（電子信箱）yanxi009＠163.com。

（編輯：羅玉蘭）