含有微孔的超彈性球體的徑向增長問題

高 洋，韋 濤

(大連民族學院理學院學生遼寧大連 116605)

含有微孔的超彈性球體的徑向增長問題

高 洋，韋 濤

(大連民族學院理學院學生遼寧大連 116605)

橡膠和類橡膠材料及其制品在現實生活中的應用非常廣泛，在使用過程中都會遇到變形、失穩、使用壽命有限以及破壞等問題，使得相關問題的研究一直是人們關注的焦點。從力學性能上講，這些材料屬于典型的非線性彈性材料范疇。關于這些材料和結構的有限變形問題的數學模型可歸結為非線性微分方程的初邊值問題。專著［1］和文獻［2］對非線性彈性材料和結構的有限變形問題和空穴問題的研究進展進行了詳實的綜述。相關的文獻還可參見文獻［3－6］。本文研究了由不可壓縮非線性彈性材料組成的含有微孔的球體在外表面受拉狀態下的有限變形問題，利用最小勢能原理求得了描述拉伸載荷與微孔增長之間關系的表達式，同時給出了相應的數值算例，并討論了材料參數和結構參數對微孔增長的影響。

1 數學模型的建立及其解

考察一個由不可壓的非線性彈性材料組成的含有微孔的球體在外表面均布的徑向拉伸載荷p0作用下的球對稱變形問題。在球坐標系下，取球殼變形前后的球坐標分別為(R，Θ，Φ)和(r，θ，φ)，球殼所占區域為其中:a和b分別為球體變形前的微孔半徑和外半徑;r(R)是待定的徑向變形函數。在球對稱變形的假設下，變形梯度張量F的主伸長λi(i=1，2，3)分別為其中c≥a是一個積分常數，它描述了含有微孔的球體變形后的徑向增長量。

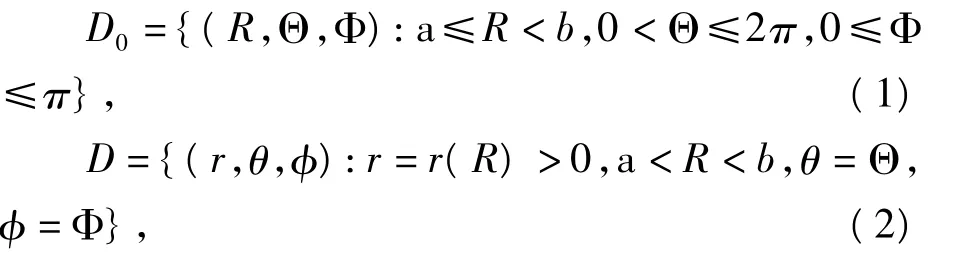
對應于球體內部空穴半徑為a的任意構形的總能量為

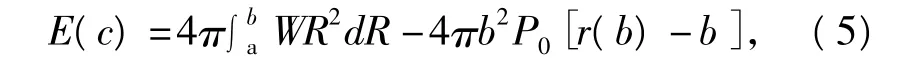
由于球體受到拉伸載荷的作用，根據最小勢能原理，球體可能的平衡位置可由Λ'(x)=0得到。經化簡可得其中:W=W(λ1，λ2，λ3)是不可壓縮非線性彈性材料的應變能函數。式(4)中的第一項是總的應變能，第二項表示外表面拉伸載荷所做的功。將式(3)和(4)代入到式(5)，并將其無量綱化，得到

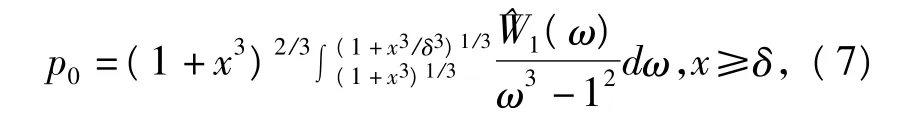
式(7)描述了不可壓縮非線性彈性材料組成的含有微孔的球體在外表面拉伸載荷p0作用下，微孔增長p0與之間的精確關系。然而對于不同的不可壓縮非線性彈性材料，微孔的增長的情況也不盡相同。

2 數值算例

本文考慮不可壓縮Gent－Thomas材料，對應的應變能函數為其中μ1，μ2是材料的無窮小變形的剪切模量。此

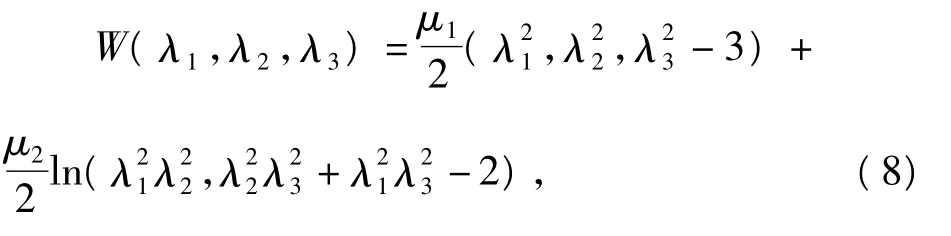
圖1 材料參數α取相對較小值時微孔半徑與拉伸載荷之間的增長關系，α=1。

由圖1可見，對于給定的材料參數和結構參數，當初始微孔半徑較小時，隨著拉伸載荷的增加，微孔增長得很慢，當載荷達到一定值時，微孔會突然增長;當初始微孔半徑相對較大時，隨著拉伸載荷的增加，微孔的增長會趨于平緩。

由圖2可見，對于給定的材料參數和結構參數，參數存在一個臨界值，當時，隨著拉伸載荷的增加，微孔的增長會趨于平緩;然而，當時，隨著拉伸載荷的增加，微孔半徑會出現跳躍性增長(這種現象可以用最小勢能原理來進行解釋)。

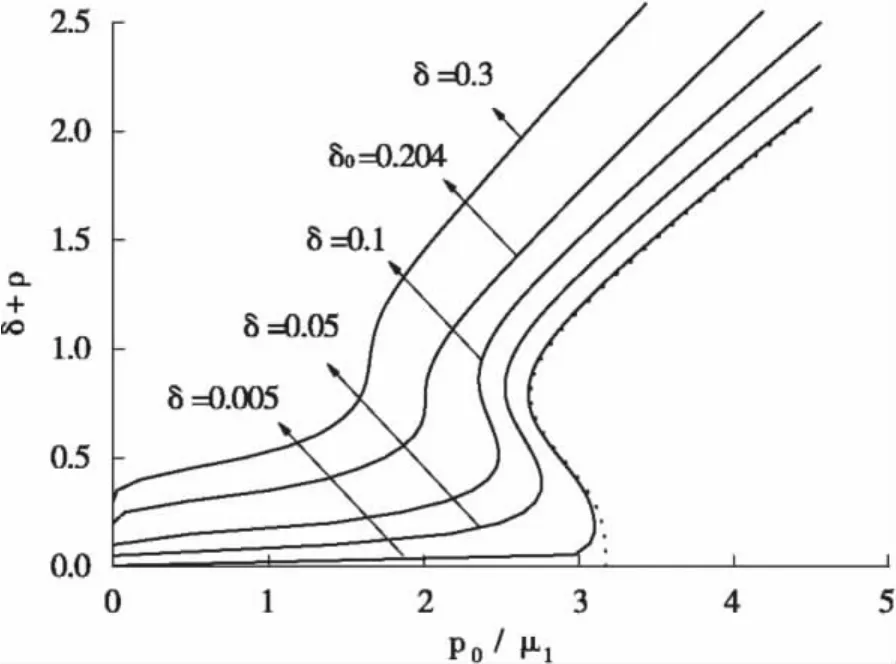
圖2 材料參數α取相對較大值時微孔半徑與拉伸載荷之間的增長關系，α=3。

［1］FU Y B，OGDEN R W.Nonlinear Elasticity:Theory and Applications［M］.London Math.Society Lecture Note Series 2001.

［2］POLIGNONE D A，HORGAN C O.Cavitation for incompressible anisotropic nonlinearly elastic spheres［J］.外應變能函數(8)也可記為對于不同的材料參數，載荷與微孔半徑的增長關系如下圖所示:Journal of Elasticity，1993，33(1):27–65.

［3］ YUAN Xuegang，ZHU Zhengyou，CHENG Changjun.Study on cavitated bifurcation problem for spheres composed of hyper－elastic materials［J］.Journal of Engineering Mathematics，2005，51(1):15－34.

［4］袁學剛.關于超彈性材料球體中空穴分岔問題的研究(Ⅰ)［J］.煙臺大學學報(自然科學版)，2005，18(2):79－90.

［5］REN Jiusheng，YUAN Xuegang.Mechanics of formation and rupture of human aneurysm ［J］.Applied Mathematics and Mechanics(English Edition)，2010，31(5):593－604.

［6］NIU Datian，ZHANG You，YUAN Xuegang，et al.Analytic Solutions of Parametric Type and Numerical Simulations of a Class of Nonlinear Ordinary Differential Equations［J］.Applied Mathematical Sciences，2010，4(30):1451－1455.

0343

A

1009－315X(2011)05－0530－02

2010－12－07;最后

2011－07－26

國家自然科學基金(10872045)。

指導教師:袁學剛(1971－)，男，吉林樺甸人，教授，博士，學校優秀學術帶頭人，主要從事數值逼近和非線性微分方程的解法等研究。

(責任編輯 劉敏)