MODIS影像的幾何處理算法研究

梁志華

MODIS影像的幾何處理算法研究

梁志華

(博羅縣國土資源局，博羅 516100)

MODIS影像的幾何處理是一項基礎性的研究工作，是數據投入使用之前的一個十分重要的環節。該文對MODIS影像邊緣區域數據重疊問題的幾何精糾正方法進行了研究。由于MODIS的大掃描角和地球曲率的影響導致了數據重疊錯位現象，通過比較已有的重疊效應去除算法的優缺點，研究了在幾何糾正過程中消除影像邊緣重疊的直接法和直接－間接法兩種重采樣方法。實驗表明，這兩種方法使重疊現象都得到了有效的去除，并且幾何精糾正精度基本符合要求，重建了真實的影像幾何特征。

MODIS數據;數據重疊;幾何精糾正

0 引言

MODIS(中分辨率成像光譜儀)是EOS AM－1(TERRA衛星)和PM－1(AQUA衛星)上搭載的主要傳感器，也是海岸帶水色掃描儀(CZCS)、甚高分辨率掃描輻射計(AVHRR)、高分辨率紅外分光計(HIRS)和專題制圖儀(TM)等傳感器的繼續，是美國對地觀測系統EOS系列衛星中最為重要的傳感器之一，在環境監測、氣象預報等方面有著重要的應用與研究價值。研制MODIS的目標是建立全球大氣、海洋和陸地的動力學模型，并能在地球發生變化之前做出準確的預測。

幾何精糾正是利用直接定位計算出來的地理坐標，對由于各種誤差導致幾何畸變的影像進行糾正的過程。MODIS 1B影像的幾何畸變包括像素的幾何形變和相鄰掃描帶的重疊。糾正像素幾何形變的過程主要包括對地理定位信息進行投影變換生成投影底圖和影像重采樣兩個步驟。對重疊效應的去除也可以在重采樣中進行處理。MODIS與其他傳感器相比，不同之處在于MODIS帶有大量的經緯度地理定位信息，可以直接用于地圖投影、生成地理格網。

在MODIS成像過程中，由于地球曲率影響和大掃描角導致掃描帶之間出現重疊錯位現象，對該現象的處理目前還沒有統一且處理得非常徹底的方法。Wolfe等［1］從宏觀上闡述了MODIS成像規律、幾何畸變和糾正處理的基本方法，但沒有提出具體有效的幾何糾正措施。郭廣猛［2］提出了非星歷表法，即利用逐行移動模板計算相關系數的方法求得重疊度，并討論了傳統的幾何糾正方法——Built GLT和Export GCP方法。這是ENVI中所采用的幾何糾正方法，但用該方法糾正MODIS影像的誤差較大。蔣耿明［3］使用了三次樣條曲線對坐標進行插值，采用前向和后向映射相結合的方式確定糾正后某一像素點在原始影像中的位置，同時使用歸一化反距離加權插值法計算糾正后像素點的屬性值，提高了糾正的精度，但沒有明確指出確定像素點位置的方法。而重疊現象的去除是用戶進一步使用1B產品的前提，因此，消除MODIS影像中重疊現象的研究工作顯得非常迫切。

本文在對比、研究前人已有的重疊效應去除算法優缺點的基礎上，提出了在幾何糾正過程中消除影像邊緣重疊的直接法和直接－間接法兩種重采樣方法。通過實驗表明，這兩種方法使重疊現象都得到了有效去除，重建了真實的影像幾何特征。

1 MODIS幾何畸變現象

MODIS是一種被動式擺動掃描探測器，其擺動掃描角為±55°。沿掃描方向，1 km空間分辨率的采樣點有1 354個，按平面距離計算，掃描帶寬應為1 354 km。由于地球曲率以及探測方式的影響，像素的大小隨掃描角的增大而增大，掃描帶寬實際達到了2 330 km。每完成一次掃描，MODIS探測器就沿軌道中心前進10 km;而在軌道兩端，掃描距離達到了20 km。因此，兩個相鄰的掃描帶在邊緣處有10 km(即50%)的數據是重復掃描了地面同一區域，這種現象被稱為數據重疊現象，也稱為“雙眼皮現象”或者“Bowtie效應”［4］(圖1，2)。

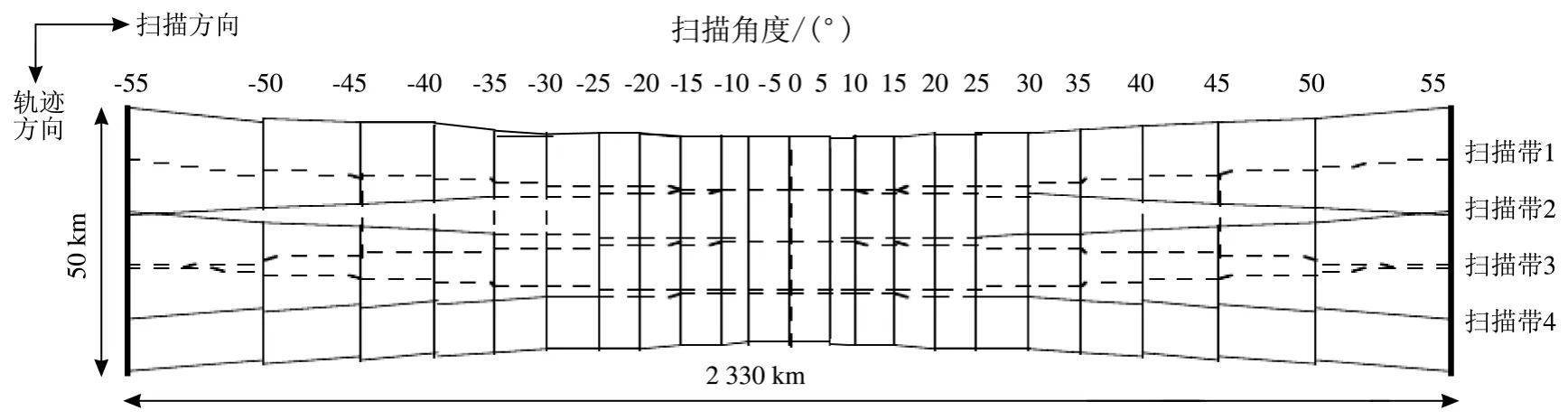
圖1 弓形扭曲效應圖Fig.1 Sketch map of bowtie distortions

圖2 MODIS數據重疊現象(空間分辨率250 m，波段2)Fig.2 Overlap graph of MODIS data

2 幾何精糾正算法

本文的幾何精糾正是指對直接定位后的MODIS數據，通過經緯度坐標插值、地圖投影和重采樣過程去除重疊現象，同時消除幾何形變的過程。

在幾何精糾正過程中，通過地圖投影將投影范圍內全部經緯度數據進行重新排列，在原始影像上相鄰掃描帶之間有重疊錯位的數據在投影過程中和其他非重疊區數據一起按照經緯度重新排列，經重采樣獲取底圖上每個格網點的屬性值。通過上述處理即可消除重疊現象。幾何精糾正算法的流程如圖3所示。

圖3 幾何精糾正流程Fig.3 Flow chart of geometric correction

圖3 中，1KM表示1 000 m空間分辨率的影像，HKM表示500 m空間分辨率的影像，QKM表示250 m空間分辨率的影像。幾何精糾正的步驟［5－8］包括:

1)讀入 HDF格式的 MODIS影像和相應的1 000 m空間分辨率的坐標數據;

2)如果影像的空間分辨率為250 m或500 m，需采用雙線性插值方法對經緯度坐標進行插值，使影像的每一個像素點都有一個坐標值與其對應;

3)投影轉換，根據我國所處的地形特點，為了保證投影后面積變形最小，采用亞爾勃斯(Albers)等積圓錐投影;

4)得到投影底圖后，給每個網格點賦予影像數值，即重采樣。

確定空間位置的方法一般分為兩種:直接法和間接法。直接法是把糾正前影像的像素逐一對應到糾正后的影像中去，通過這樣的處理會出現空缺現象，造成糾正后影像的不連續。間接法是把糾正后影像的像素逐一映射到糾正前的影像中去，糾正后影像的每一個像素都能在糾正前的影像中找到對應像素，可以避免直接法所造成的不連續性。但是由于MODIS影像在空間分布上的特殊性，像素在空間上分布是不均勻的，并且彼此重疊，傳統的間接法在尋找映射點方面產生了無法克服的困難——在星下點影像區域，MODIS相鄰掃描條帶彼此不存在重疊，在原始影像上得到的映射點是唯一的;而隨著觀測角度的增大，相鄰掃描條帶之間出現重疊，在原始影像上得到的映射點有兩個，并且這兩個映射點的位置不能直接被獲取，即使找到了映射點，要找到參與插值計算的像素點也存在困難(這主要是因為參與插值的原始像素點可能與映射點同條帶，也可能位于相鄰條帶上)。為了解決這一難題，本文研究了直接法和直接－間接法這兩種方法，從而確定像素的空間位置，進行幾何精糾正。

2.1 直接法

經過投影之后，影像上的點陣有些會顯得相對稀疏，有些則相對密集。密集的區域代表相鄰兩條掃描帶上重疊區域的投影。有些特別稀疏的地方會出現無值的空點，該空點表示經緯度坐標投影不到的地方。對這些密集和稀疏的地方需要分開進行屬性處理。直接法流程見圖4。

圖4 直接法流程圖Fig.4 Flow chart of direct method

將原始影像上的每個原始點D(i，j)投影到底圖上得到對應點坐標值S(x，y)，接著計算投影點所在格網S(a，b)的屬性值。對每一格網，首先搜索在該格網內的投影點個數，并計算投影點距格網中心的距離，對該格網內搜索到的所有投影點通過距離倒數加權法插值，插值得到的屬性值即為該格網的屬性值;其次若該格網內搜索不到投影點，則搜索該格網周圍3像素×3像素窗口范圍內的投影點個數，并計算搜索到的投影點距格網中心的距離，對搜索到的多個投影點通過距離倒數加權的方法插值，插值得到的屬性值即為格網的屬性值;然后對于邊緣部分區域，投影之后的空白無值點范圍比較大，若采用3像素×3像素窗口搜索不到投影點，則采用5像素×5像素窗口進行搜索，然后對搜索到的投影點插值;最后若采用5像素×5像素窗口也搜索不到投影點，則設定一個閾值，尋找距離該格網在閾值范圍內最近的點，將最近點的屬性值賦予該格網，以保證圖像輸出結果的最大準確性。因為投影前的經緯度坐標與投影后的不規則點坐標之間是一一對應的，所以通過上述插值處理，投影后底圖上將不再出現重疊現象。

通過以上步驟可以去除重疊現象的原因是，通過投影過程將投影范圍內全部經緯度數據重新進行排列，在原始圖像上相鄰掃描帶之間有重疊錯位現象的數據在投影過程中相應地和其他非重疊區數據一起按照經緯度重新排列，投影后每一格網對應唯一的平面坐標，因此在投影之后的圖像上基本不會再看到bowtie效應。

2.2 直接－間接法

直接－間接算法的流程見圖5。

圖5 直接－間接法流程圖Fig.5 Flow chart of direct－ indirect method

首先將原始影像上的每一像素D(i，j)投影到底圖上得到對應的坐標值S(x，y)，根據投影后坐標值和底圖上行列間距值，判斷該投影點所在格網的行列號S(a，b);其次對格網周圍3像素×3像素范圍內的像素進行反投影，得到原始圖像上的經緯度坐標值D(lon，lat)，一般情況該經緯度坐標值分布在像素D(i，j)附近;再次以像素D(i，j)為中心構建2像素×2像素窗口M，判斷坐標值D(lon，lat)是否落在該范圍內，若搜索到的結果為“是”，則對窗口M內的4個像素進行插值，若搜索到的結果為“否”，則以像素D(i，j)為中心構建4像素×4像素窗口M，繼續搜索;然后利用搜索到的像素進行插值，采用距離反比插值方法計算搜索到的像素在投影底圖上距離格網點的距離，通過插值得到格網點的屬性值;最后將得到屬性值的格網點標記為1，以免下次重復參與插值。接著對原始影像的下一個像素按照上述流程進行處理，依次類推。

該算法充分利用了原始影像上相鄰像素間的相關性，使影像上的重疊錯位現象去除得比較徹底，與直接法相比影像信息更為豐富。

3 算法實現與分析

對250 m空間分辨率的MODIS數據利用直接法和直接－間接法兩種重采樣方式進行幾何精糾正后，全景影像見圖6。

圖6 MODIS數據糾正前后的全景影像圖(空間分辨率250 m，波段2)Fig.6 Comparison of MODIS data before and after correction

在圖6中，(a)為糾正前MODIS原始影像圖，(b)為采用直接法進行幾何精糾正后的影像圖，(c)為采用直接－間接法進行幾何精糾正后的影像圖，投影方式為Albers等面積圓錐投影(第一標準緯線圈:25°;第二標準緯線圈:47°;中央經線:105°)。顯示重疊現象更加清楚的局部放大影像見圖7。

圖7 MODIS數據(局部)糾正前后對比(空間分辨率250 m，波段2)Fig.7 Comparison of MODIS data(local)before and after local correction

從圖7中可以看出，利用本文提出的直接法和直接－間接法進行幾何精糾正，糾正后的影像完全消除了幾何畸變，重疊現象明顯得到了改善，清晰地重建了真實的影像幾何特征。

由于兩種算法投影方式相同，并且投影之后在底圖上的空間定位方法也相同，故幾何精糾正的精度是一樣的。

在用直接－間接法對250 m空間分辨率的MODIS影像進行幾何精糾正的基礎上，對其結果影像進行了精度分析(表1)。

表1 幾何校正精度Tab.1 Accuracy of geometric correction

1 000 m空間分辨率影像的幾何精糾正精度主要取決于 MODIS探測器對空間定位的精度，而250 m和500 m空間分辨率影像的幾何精糾正精度不僅取決于探測器的空間定位精度，而且還取決于坐標插值的精度。本文所述的處理流程中，影響幾何精糾正精度的過程主要有經緯度插值和數據重采樣插值。雙線性插值和距離倒數加權插值法在理論上是比較準確的方法，而且符合經緯度和地物光譜的分布規律;由于是內插，所以處理后誤差不會超過原誤差值。定位之后沒有通過地面控制點改正，對250 m空間分辨率影像的定位誤差大約為1個像素，通過表1可以看到幾何精糾正誤差基本達到要求。

4 結論

本文對MODIS影像中存在的問題——數據重疊現象形成的原因進行了分析，并在總結前人研究的基礎上提出了在幾何精糾正過程中消除重疊現象的解決方案，設計了實驗流程，并對實驗處理的結果進行了分析，取得如下主要成果:

1)通過分析MODIS影像產生邊緣重疊現象的原因，提出了在幾何精糾正過程中消除重疊現象的兩種重采樣方法——直接法和直接－間接法，采用這兩種方法都可以有效地去除重疊現象，幾何糾正的精度也基本達到要求。

2)幾何精糾正過程中，像素重采樣時的插值方法采用距離反比加權插值方法，證明了該方法對地理空間這種互相之間存在相關現象的空間插值而言是比較精確的。

進行幾何精糾正時，重采樣過程中采用直接法和直接—間接法得到的影像與原影像相比，整體被平滑，損失了細節部分，這是由插值引起的，故對插值算法還需進一步改進。MODIS數據的處理是一項復雜的系統工作，本文僅僅涉及其中很小的一部分，對于條帶噪聲的處理、太陽高度角的訂正等研究還有待進一步開展。

［1］ Wolfe R E，Nishihama M，Fleig A J，et al.Achieving Sub － pixel Geolocation Accuracy in Support of MODIS Land Science［J］.Remote Sensing of Environment，2002，83(1/2):31 －49.

［2］ 郭廣猛.非星歷表法去除MODIS圖像邊緣重疊影響的研究［J］.遙感技術與應用，2003，18(3):172 －175.

［3］ 蔣耿明.MODIS數據基礎處理方法研究和軟件實現［D］.北京:中國科學院研究生院，2003.

［4］ Günther K P，Maier S W，Gesell G.MODIS－ receiving and Processing at DFD［M］.DFD － Nutzerseminar，2002:83 －93.

［5］ 衛 東.MODIS數據的高精度定位方法研究［D］.北京:清華大學，2003.

［6］ 徐 萌，郁 凡.去除EOS/MODIS 1B數據中“彎弓”效應的方法［J］.氣象科學，2005，25(3):257 －264.

［7］ 郭廣猛.關于MODIS衛星數據的幾何校正方法［J］.遙感信息，2002(3):26－28.

［8］ 李柳霞.MODIS影像數據預處理技術研究［D］.北京:中國農業大學，2004.

A Study of Algorithm of Geometric Processing for MODIS Image

LIANG Zhi－hua
(Land and Resources Bureau，Boluo 516100，China)

The geometric process of MODIS image is a kind of basic research work and is a key step before the utilization of data.In view of the fact that the large scanning angle of MODIS and the earth’s curvature lead to the overlapping and dislocation，this paper deals in detail with high precision location and geometric correction for MODIS data.Based on a comparative study of the advantages and disadvantages in some overlapping removing algorithms，the author presents the direct method and direct－ indirect method which can remove overlap in geometric correction.It is proved that the two kinds of resampling methods are feasible，and the precision of geometric correction can basically meet the requirement.Thus，the real image geometric character is rebuilt.

MODIS data;data overlay;geometric correction

TP 751.1;P 237

A

1001－070X(2012)01－0008－05

10.6046/gtzyyg.2012.01.02

2011－04－27;

2011－06－09

梁志華(1987－)，女，碩士，研究方向為“3S”技術與數字國土。E－mail:cathylzh@126.com。

(責任編輯:邢 宇)