穿越公路輸氣管道力學性狀影響因素研究

蘭國冠,趙向前,孫安勇

(1.三明學院建筑工程學院,福建三明 365004;2.中節能建設工程設計院有限公司,四川成都 610052; 3.成都博銳建筑工程咨詢有限公司,四川成都 610001)

0 引 言

通常,車輛荷載作用下埋地輸氣管道的動力響應涉及多個學科,如道路工程、管道工程、車輛工程、巖土工程以及彈塑性力學、土力學、結構力學、隨機振動理論等,是一個跨學科的交叉研究課題,用純理論方法研究難度很大,而試驗研究需要花費大量的人力、財力,且解析計算不能很好地解決復雜問題[1-5],數值模擬技術的出現恰好彌補了上述不足,有限元、邊界元等數值方法逐漸流行,并成為工程計算領域中的最重要手段之一[6-10].本研究利用理論分析結合ANSYS模擬軟件對穿越公路輸氣管道在車輛荷載作用下的力學性狀進行數值模擬與分析.

1 車輛移動方向與管道垂直時的管土受力模型

車輛移動方向與管道垂直時的管土受力模型描述的是當移動荷載方向與管道垂直交叉時的受力情形.由于地基土體是一個無限空間體,在計算中本研究截取一定的范圍,確定地基的三維固體有限元計算模型尺寸為,長×寬×高=10 m×5 m×5 m,軟土地基的密度為1 790 Kg/m3,彈性模量為9 MPa,泊松比0.40.管道為三維固體模型,長度10 m,壁厚25 mm,埋深2 m,管道材質為鋼材,密度為7 850 Kg/ m3,彈性模量為210 GPa,泊松比0.30.管道邊界條件為兩端設為固支.荷載大小為四分之一車重,為點荷載作用在車輪軌跡上,這里把車輪軌跡視為兩條直線.

1.1 車輛模擬參數

本研究中,車輛具體模擬參數如表1所示.

表1 車輛模擬參數

1.2 土體材料參數

土體模型選用與實際土體彈塑性狀態較接近的Drucker-Prager模型.該模型服從廣義的Von-Mises屈服準則,其表達式[8]為:

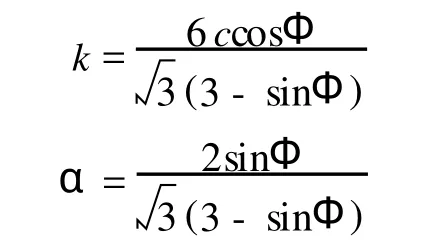
土體具體參數如表2所示.

表2 土體具體參數表

1.3 管道材料參數

本研究采用的管道為X70級管材,利用雙線形硬化彈塑模型,該模型遵從Von-Mises屈服準則,其表達式[8]為,

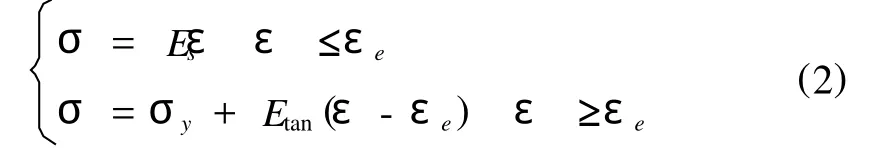
式中,σ為應力;σy為屈服應力;Es、Etan為彈性模量和切線模量;ε、εe為應變和彈性極限應變.

埋地輸氣管道具體參數如表3所示.

表3 埋地輸氣管道參數

1.4 選取單元類型及網格劃分

本研究采用Solid 45及Solid 65單元來模擬土體和埋地管道.Solid 45單元由8個節點結合而成,每個節點有xyz 3個方向自由度,該單元具有塑性、蠕變、膨脹、應力強化、大變形、大應變等特征.Solid 65單元為8節點6面體單元,是和普通的8節點空間實體單元Solid 45相同的實體單元模型,但加入了Willam-Warnke 5參數破壞準則.

對建立的幾何模型,需要對其劃分網格生成包含節點和單元的有限元模型.有限元網格的劃分過程包括3個步驟[9-10]:①定義單元屬性,包括指定單元類型、分配實常數、分配材料屬性等;②設置網格控制(可選擇的);③生成網格.

選用有限元計算時,單元網格劃分越密,計算誤差越小,越接近于真實值,不過網格劃分越密計算時間就越長,計算量越大.地基及管道網格劃分如圖1、2所示.

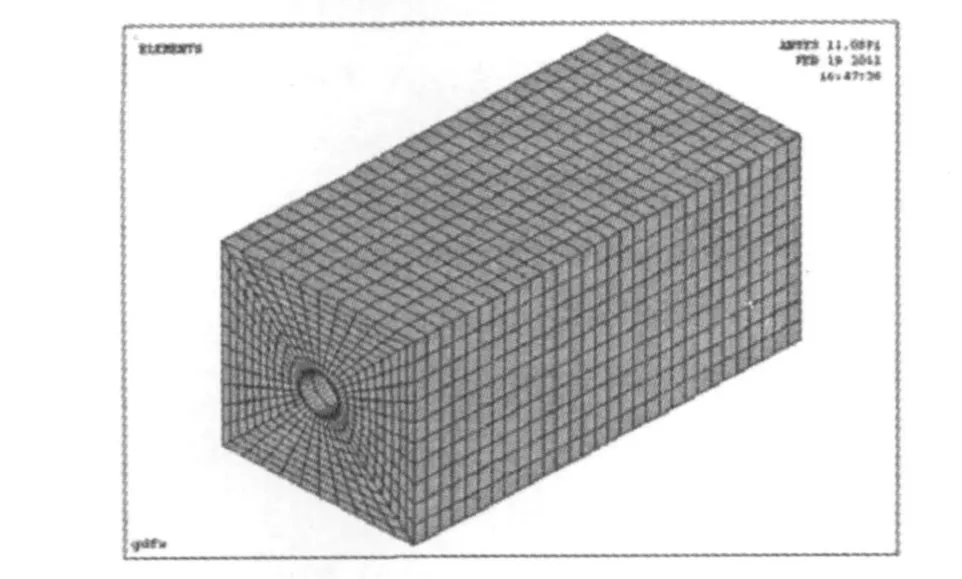
圖1 管土模型及土體模型單元網格劃分圖

2 不同因素對管道應力的影響分析

2.1 車速對管道應力的影響

2.1.1 把管道中點作為研究對象,研究車速對管道應力的影響.

為了分析車輛速度對管道中點應力的影響,假設路面近似平整,在保證其他因素不變的情況下分別選取20 km/h、30 km/h、40 km/h、50 km/h、60 km/h 5個不同的車速進行模擬.取得不同車速下管道中點的應力峰值,即得管道中點Mises應力隨車速變化趨勢圖如圖3所示.

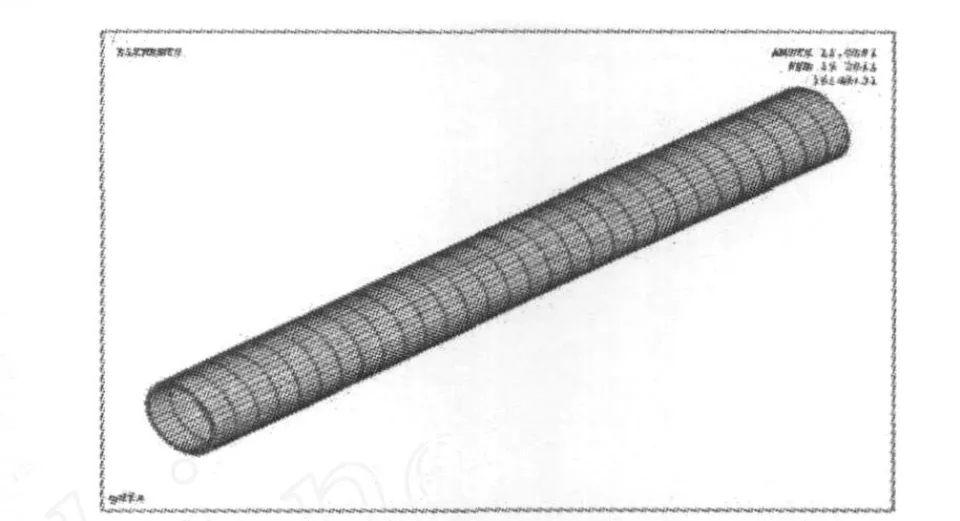
圖2 橫穿公路管道模型邊界及單元網格劃分圖

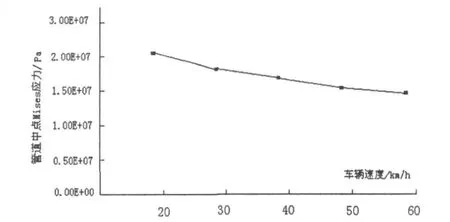
圖3 管道中點Mises應力峰值隨車速變化趨勢圖

由圖3可以看出:在路面近似平整的情況下,隨著車速的增大,管道受到的應力呈減小趨勢,不過當車速超過45 km/h后,管道中點Mises應力變化不大,其原因是地基中的應力傳遞需要依靠相鄰的顆粒來完成,車輛速度大,應力出現的時間就短,從而來不及向土體周邊傳遞,應力響應特征就不那么顯著.

2.1.2 把管道中點作為研究對象,研究車速對管道變形的影響.

與研究應力隨車速變化一樣,在保證其他因素不變的情況下分別選取20 km/h、30 km/h、40km/h、50 km/h、60 km/h 5個不同的車速進行模擬.取得不同車速下管道中點的變形峰值,即得管道中點變形隨車速變化趨勢圖如圖4所示.

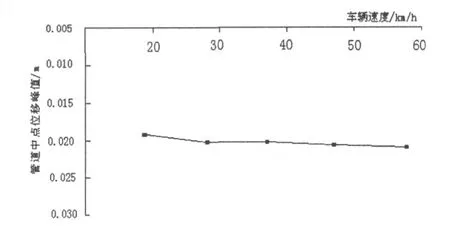
圖4 管道中點位移峰值隨車速變化趨勢圖

由圖4可以看出,不同車速下,管道中點的位移響應相差不大,基本呈一條水平直線,此表明,車輛速度變化對管道變形的影響不是很大.

2.2 車輛載重的影響

為了研究車輛載重對管道應力及變形的影響,假定其他參數不變,選用一組不同載重的車輛模型,由于本研究假設車輛加載為點荷載,車輛以4個車輪計算,因此把四分之一車載重作為點荷載值.分別選用8 t、9 t、10 t、13 t、16 t 5種不同載重的車輛進行模擬,折算成四分之一點荷載分別為,F1=20 000 N、F2=22 500 N、F3=25 000 N、F4=32 500 N、F5= 40 000 N.對此,管道中點應力與位移隨車載重變化趨勢圖如圖5、6所示.

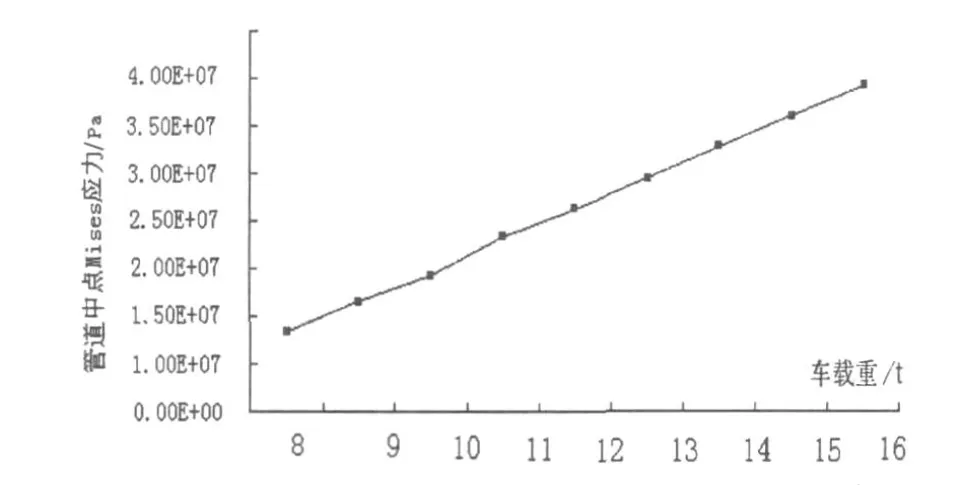
圖5 管道中點Mises應力峰值隨車輛載重變化趨勢圖

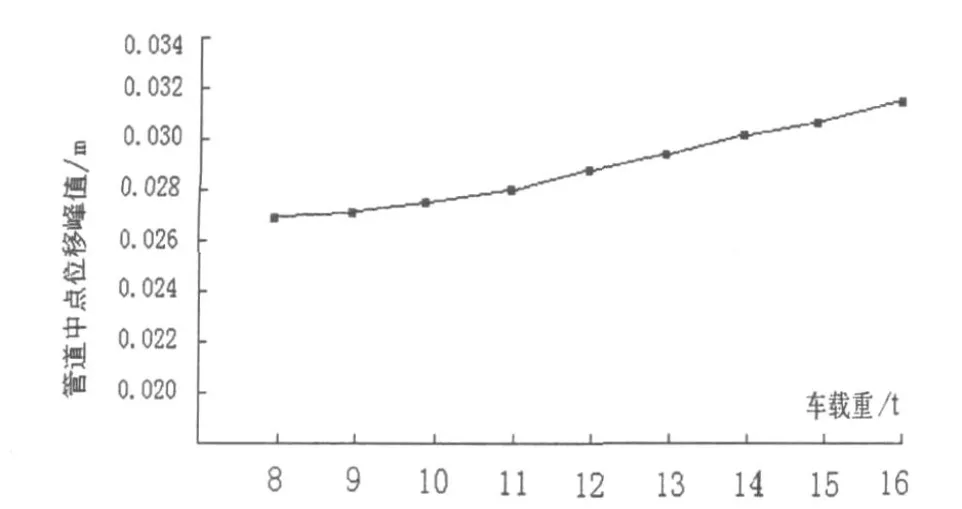
圖6 管道中點位移峰值隨車輛載重變化趨勢圖

由圖5可以看出,管道中點Mises應力隨車輛載重的增大而大致線性增大.由圖6可以看出,當車輛載重從8 t逐漸增加到16 t的過程中,管道中點位移峰值變化幅度不大,僅變化0.003 m左右.同時,研究中還發現,隨著車輛載重的增加,位移的波動減小,其原因是管道所受壓力增加時,其所受的約束也相應增加,從而使位移的波動減小.

2.3 管道直徑的影響

在研究管徑對管道位移的影響時,保持車速及其他參數不變,分別選用3種不同管徑(D=0.9 m, D=1.1 m,D=1.3 m)的管道進行模擬,最后取各管徑對應的管道中點位移響應量峰值,即得位移響應峰值隨管徑變化趨勢繪成圖表如圖7所示.

圖7 管道中點位移響應峰值隨管徑變化圖

由圖7可以看出,隨著管徑的增大管道位移響應量減小,不過從0.9 m變化至1.1 m時,管道位移值變化量比從1.1 m變化至1.3 m時小得多.

2.4 管道埋深的影響

管道中點應力峰值隨深度變化趨勢如圖8所示.

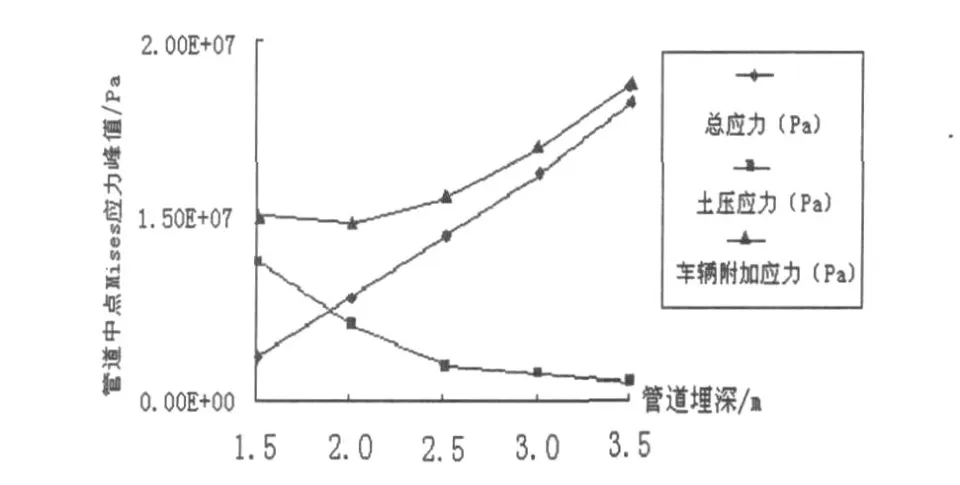
圖8 管道中點應力峰值隨深度變化趨勢圖

由圖8可以看出,土體壓力隨著埋深的增加而線性增大,而車輛產生的附加應力則隨著埋深的增加而快速減小,其原因在于土體的阻尼特性及擴散作用使車輛產生的附加應力在深處漸漸消散,所以管道所受總應力就呈現先減小后增大的趨勢.根據總應力最小的原則,我們可以確定一個最佳管道埋深,如圖8所示,最佳埋深為2 m左右.當然,在實際工程中確定最佳埋深時,還要考慮不同規格管道對其埋深的專業要求及經濟指標等因素,綜合評定.而且剛性管道與柔性管道的埋深要求是不同的,實際工程應用時應注意二者的區別.

2.5 地基彈性模量的影響

在保持其他參數不變的情況下,分別選用地基彈性模量為,E=8 Mpa、E=10 Mpa、E=12 Mpa、E= 14 Mpa、E=16 Mpa,進行模擬,管道中點Mises應力峰值與位移峰值隨地基彈性模量變化如圖9、10所示.

由圖9可知,應力峰值隨著地基彈性模量的增大而呈減小趨勢,大致成反比例關系.

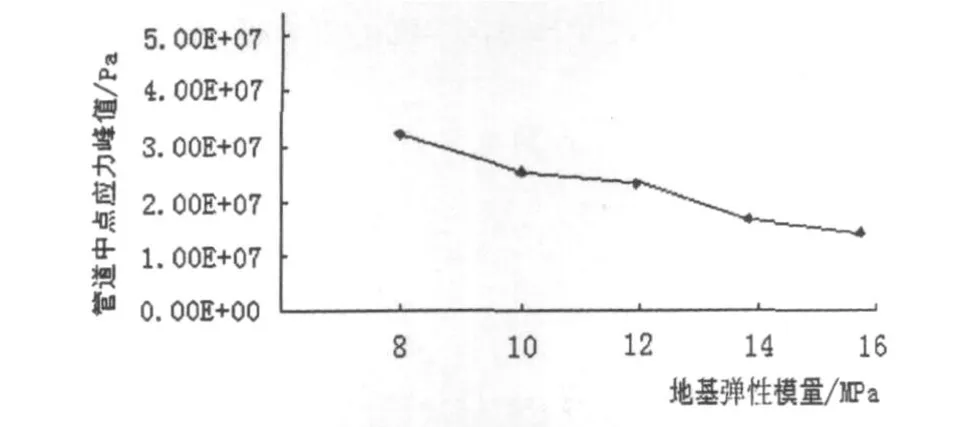
圖9 管道中點Mises應力峰值隨地基模量變化趨勢圖

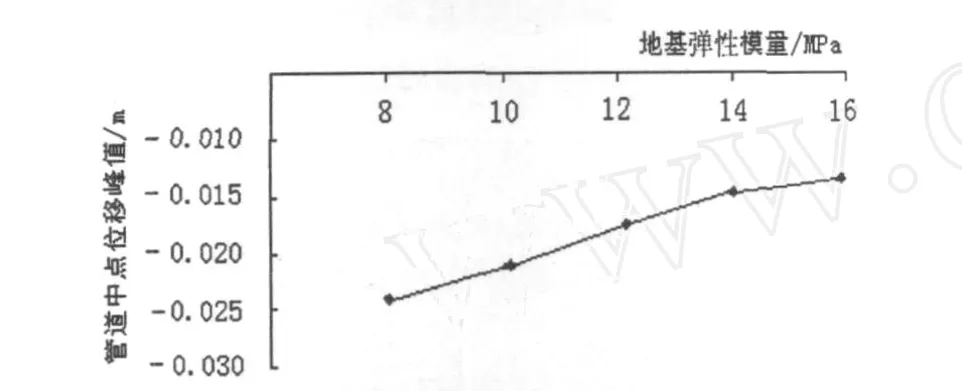
圖10 管道中點位移峰值隨地基變形模量變化趨勢

由圖10可知,位移隨地基模量變化趨勢與應力圖類似,都是大致成反比例的關系,地基彈性模量越大,管道位移量越小.

2.6 地基泊松比的影響

管道中點Mises應力峰值及位移隨地基泊松比變化趨勢如圖11、12所示.

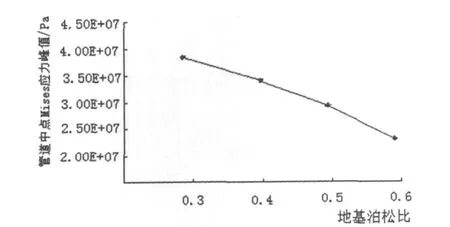
圖11 管道中點Mises應力峰值隨地基泊松比變化趨勢

由圖11可知,隨著泊松比的增大,管道應力峰值減小,且影響幅度較大,說明泊松比是影響車輛荷載作用下管道應力值的重要因素.

圖12 管道中點位移峰值隨地基泊松比變化趨勢

由圖12看出,管道中點位移峰值隨泊松比的變化與應力變化類似,隨著地基泊松比的增大,位移峰值逐漸減小.管道中點位移值與地基泊松比大致成反比例關系.

3 結 語

本文通過軟件數值模擬,得到了橫穿道路管道受車輛荷載作用時管道中點應力及豎向位移隨時間變化的時程圖等,并對影響管道力學性狀的各種因素進行了分析和總結,各因素的影響概述如下:

(1)隨著車速的增大,管道受到的應力呈減小趨勢,不過當車速超過45 km/h后,管道中點Mises應力變化不大,其原因是地基中的應力傳遞需要依靠相鄰的顆粒來完成,車速大,應力出現的時間就短,從而來不及往土體周邊傳遞,應力響應特征就不那么顯著.

(2)管道中點Mises應力隨車輛載重的增大而大致線性增大,隨著車輛質量的增加,位移的波動減小.

(3)隨著管徑的增大管道位移響應量減小,且在相同管徑級差時,較大管徑之間的位移響應量更小.

(4)土體壓力隨著埋深的增加而線性增大,而車輛荷載產生的附加應力則隨著埋深的增加而快速減小,所以管道所受總應力就呈現先減小后增大的趨勢,根據總應力最小的原則,可以確定一個最佳管道埋深,在本例中所示,最佳埋深為2 m左右.

(5)管道應力峰值隨著地基模量的增大而呈減小趨勢,大致成反比例關系.

(6)管道中點位移值與地基泊松比大致成反比例關系.

[1]候忠良.地下管線抗震[M].北京:學術書刊出版社,1990.

[2]鄧學鈞,孫璐.車輛—地面結構系統動力學[M].北京:人民交通出版社,2000.

[3]吳為義.垂直荷載作用下軟粘土地基中管道的縱向力學性狀研究[D].杭州:浙江大學,2000.

[4]李詢.交通荷載作用下埋地管道的力學性狀分析[D].浙江大學,2004.

[5]周華飛,蔣建群,毛根海.路面不平整引起的車輛動荷載分析[J].中國市政工程,2002,99(3):10-13.

[6]徐建平,尚剛,梁乃興.路面不平整引起的汽車動荷載計算分析[J].重慶交通學院學報,2001,20(1):26-28.

[7]吳小剛.交通荷載作用下軟土地基中管道的受力分析模型研究[D].杭州:浙江大學,2004.

[8]趙師平,曾祥國.第三方荷載作用下埋地輸氣管道動力響應的數值模擬[J].四川建筑科學研究,2009,35(1):134-139.

[9]劉全林,楊敏.地埋管與土相互作用分析模型及其參數確定[J].巖土力學,2004,25(5):728-731.

[10]張土喬,陳觀勝.垂直荷載作用下管道的受力模式研究[R].杭州:浙江大學土木系、杭州市市政工程總公司, 1999.

[11]張方銳.ANSYS 8.0應用基礎與實例教程[M].北京:電子工業出版社,2006.