基于Matlab的共軛平行分度凸輪的分析計(jì)算

高 英，王蕊照，鈔紅曉，王開政

（西北機(jī)電工程研究所 陜西 咸陽 712000）

平行分度凸輪是用于兩平行軸間的一種間歇傳動(dòng)機(jī)構(gòu)，具有傳動(dòng)平穩(wěn)、承載能力大等優(yōu)點(diǎn)。某機(jī)構(gòu)分度凸輪為3分度，傳動(dòng)、結(jié)構(gòu)設(shè)計(jì)決定了該凸輪驅(qū)動(dòng)角范圍為49°～52°，這與以往工程應(yīng)用中至少90°驅(qū)動(dòng)角的情況有很大不同。驅(qū)動(dòng)角過小帶來的問題首先是曲線輪廓難以設(shè)計(jì)，部分參數(shù)選擇在傳統(tǒng)設(shè)計(jì)手冊(cè)上無法查到；其次是壓力角過大，工況惡劣，在高速運(yùn)轉(zhuǎn)的情況下很容易造成沖擊變形。該機(jī)構(gòu)每一個(gè)運(yùn)動(dòng)循環(huán)凸輪分度機(jī)構(gòu)作一次分度運(yùn)動(dòng)，凸輪旋轉(zhuǎn)一周，凸輪轉(zhuǎn)速很高，而平行分度凸輪機(jī)構(gòu)一般是在中低速情況下工作[1-2]。這些都決定了該凸輪機(jī)構(gòu)設(shè)計(jì)的難度。

1 平行分度機(jī)構(gòu)的基本設(shè)計(jì)方法

1.1 滾子盤與分度凸輪運(yùn)動(dòng)關(guān)系

平行分度凸輪機(jī)構(gòu)工作原理圖如圖1所示。平行分度凸輪設(shè)計(jì)的初始條件一般包括表所示的運(yùn)動(dòng)參數(shù)和幾何參數(shù)如表1所示。

θ與φ關(guān)系是θ對(duì)φ二階導(dǎo)數(shù)連續(xù)，該自動(dòng)機(jī)射速較高，故選用適合高速運(yùn)動(dòng)的改進(jìn)正弦曲線規(guī)律[3]，方程如下：

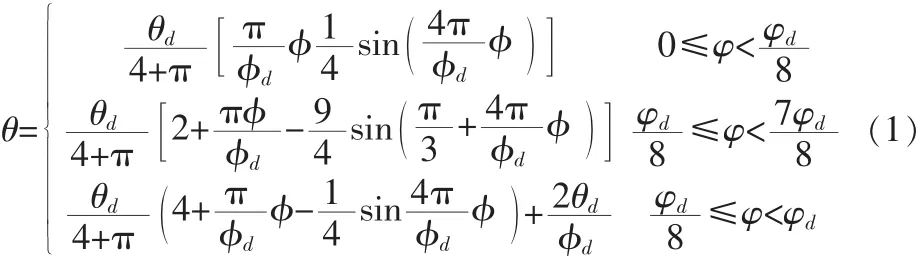
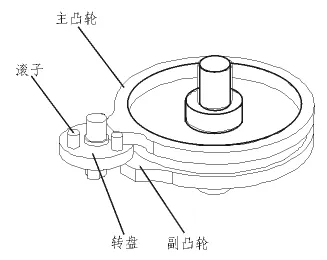
圖1 平行分度凸輪結(jié)構(gòu)圖Fig.1 Parallel indexing mechanism structure diagram

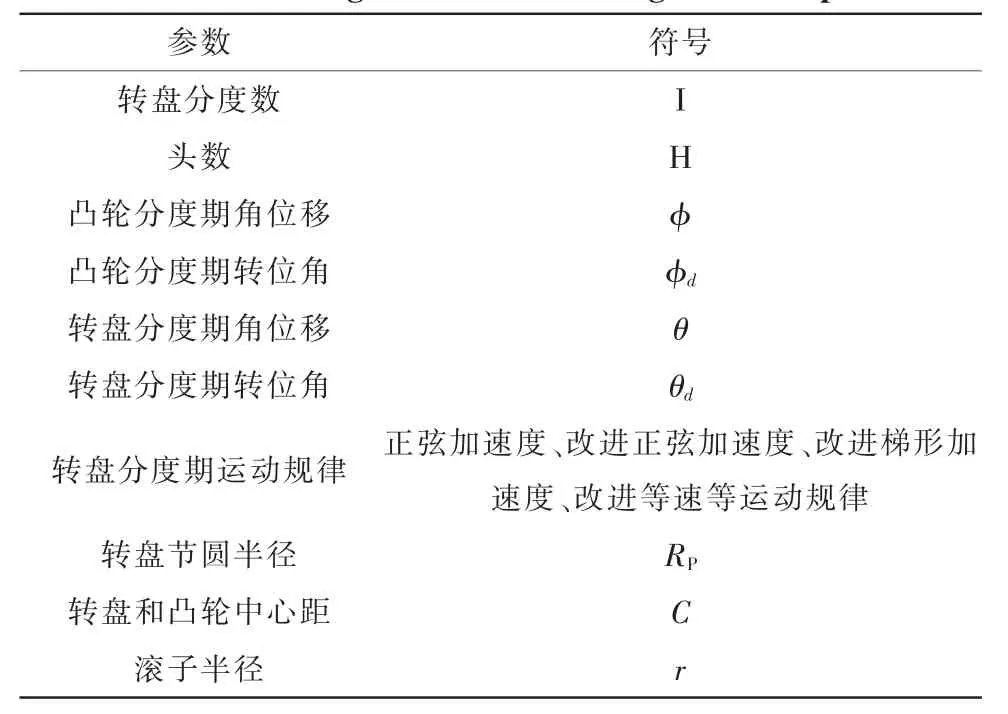
表1 平行分度凸輪運(yùn)動(dòng)參數(shù)和幾何參數(shù)Tab.1 Parallel indexing cam movement and geometrical parameters

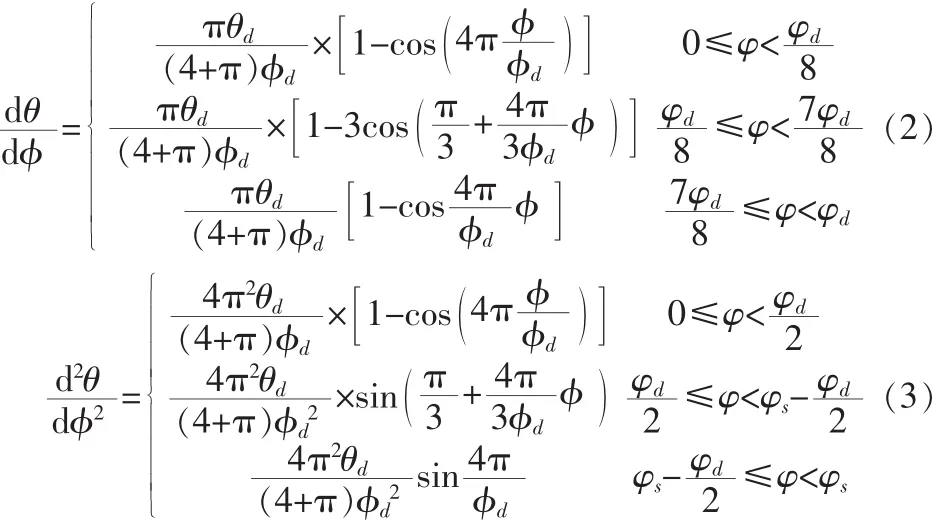
1.2 分度凸輪輪廓計(jì)算

1.2.1 凸輪理論輪廓計(jì)算

建立兩坐標(biāo)系XOY和 X1OY1，XOY為固定坐標(biāo)系，X1OY1為順時(shí)針旋轉(zhuǎn)坐標(biāo)系，即它固定在凸輪上，隨凸輪旋轉(zhuǎn)與XOY夾角為φ，如圖2所示。

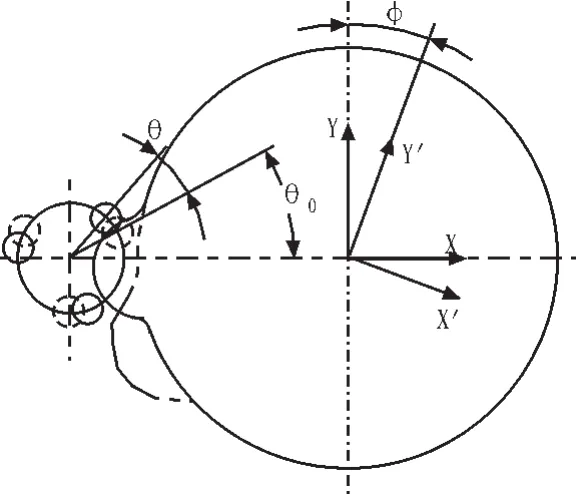
圖2 平行分度凸輪機(jī)構(gòu)解析法計(jì)算示意圖Fig.2 Diagram of parallel indexing cam mechanism analytic calculation

當(dāng)從動(dòng)輪旋轉(zhuǎn)，在XOY坐標(biāo)下從動(dòng)輪滾柱中心移動(dòng)軌跡如下式：

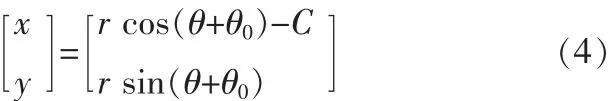
θ0為滾柱的初始角度。

在X1OY1坐標(biāo)下從動(dòng)輪滾柱中心移動(dòng)軌跡如下式

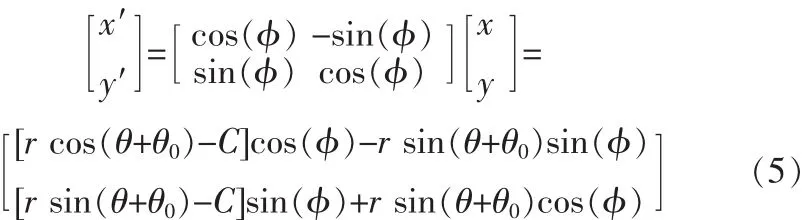
上式就是凸輪的理論輪廓曲線，φ和θ的關(guān)系確定后，上式就是關(guān)于的參數(shù)方程。

1.2.2 凸輪實(shí)際輪廓計(jì)算

凸輪的理論輪廓曲線是沿實(shí)際輪廓曲線的法線方向偏移滾柱半徑r距離[4]。由于理論輪廓曲線和實(shí)際輪廓曲線對(duì)應(yīng)點(diǎn)上法線方向是相同的，故可用理論輪廓曲線沿其法線方向偏移滾柱半徑r得到實(shí)際輪廓曲線。

由下式計(jì)算實(shí)際輪廓曲線，也是關(guān)于φ的參數(shù)方程

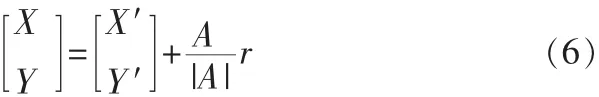
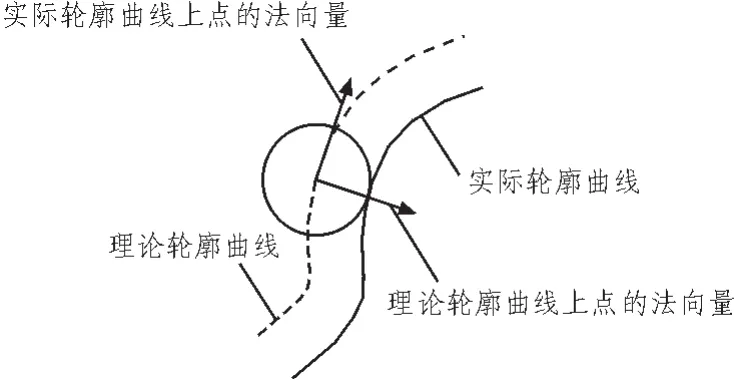
圖3 實(shí)際輪廓線和理論輪廓線的關(guān)系Fig.3 Relationship between the actual contour and the theoretical contour

2 示例與仿真

依據(jù)以上的設(shè)計(jì)方法，利用MATLAB編寫了仿真程序，并采用GUI Builder編寫了仿真界面，便于參數(shù)化設(shè)計(jì)[5]。機(jī)構(gòu)的基本參數(shù)以及選擇的運(yùn)動(dòng)規(guī)律是：中心距C=65 mm，RP=11 mm，滾子半徑 r=5 mm，φd=52°，選取改進(jìn)正弦運(yùn)動(dòng)規(guī)律，計(jì)算仿真結(jié)果如圖4所示。

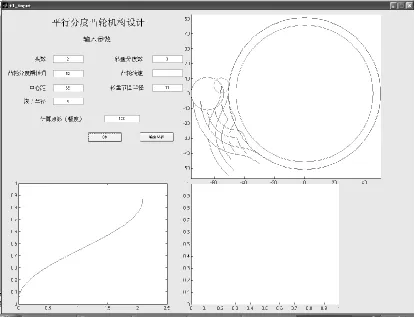
圖4 仿真計(jì)算結(jié)果Fig.4 Simulation results

3 結(jié) 論

文中提出了一種利用Matlab變成實(shí)現(xiàn)平行分度凸輪設(shè)計(jì)，利用GUI Builder編寫了仿真界面，解決了工程實(shí)際中的難題[6]。采用該方法有以下幾個(gè)突出優(yōu)點(diǎn)：1）該方法通用性強(qiáng)，可以計(jì)算多種形式的平行分度凸輪；2）采用圖形顯示，設(shè)計(jì)結(jié)果一目了然，具有良好的人機(jī)界面；3）計(jì)算得到的數(shù)據(jù)直接輸出為文本文件，導(dǎo)入三維設(shè)計(jì)軟件即可完成建模；4）完整的參數(shù)化設(shè)計(jì)，便于調(diào)整參數(shù)進(jìn)行對(duì)比分析。

[1]王中發(fā).機(jī)械設(shè)計(jì)[M].北京：北京理工大學(xué)出版社，1998.

[2]張志涌.精通MATLAB（5.3）版[M].北京：航空航天大學(xué)出版社，2000.

[3]彭國勛，肖正揚(yáng).自動(dòng)機(jī)械的凸輪設(shè)計(jì)[M].北京：北京理工大學(xué)出版社，1990.

[4]付瑩瑩.平行分度凸輪輪廓解析設(shè)計(jì)新方法及其應(yīng)用[J].機(jī)床與液壓，2009，37（5）：152-154 FU Ying-ying.A new analytical design method of parallel indexing cam contour and its application[J].Machinetool&Hydraulics，2009，37（5）:152-154

[5]鄒慧君，殷鴻梁.間歇運(yùn)動(dòng)機(jī)構(gòu)設(shè)計(jì)與應(yīng)用創(chuàng)新[M].北京：機(jī)械工業(yè)出版社，2008.

[6]張賢明.MATLAB語言及應(yīng)用案例[M].江蘇：東南大學(xué)出版社，2010.