基于兩棱鏡模型的盾構引導系統開發與研究

王 智

（青島市勘察測繪研究院，266032，青島∥工程師）

目前國內地鐵施工中獲取盾構機的實時姿態主要采用人工測量手段，耗時且費力，且使用的自動引導系統均是從國外引進，如德國VMT公司的SLS系統及日本的小松系統等。國內一些單位研究的自動引導系統基本都處于試驗階段，且普遍是三棱鏡模型。它是基于空間直角坐標轉換或根據空間相應特征點距離不變的特性解算方程組來求取盾首盾尾的坐標。當曲率半徑比較小時，吊籃上的全站儀會出現不能同時觀測到3個棱鏡的情形。針對這種情況，提出在盾構機上適當的位置安置2個棱鏡和1個雙軸傾斜儀來獲取盾構機姿態的方法。

開發的兩棱鏡引導系統的運行流程如下：

（1）在始發井中在盾構機上適當位置焊接2個棱鏡，嚴格測定2個棱鏡和盾首盾尾的位置關系，并在盾構機上安置一個電子雙軸傾斜儀；

（2）在系統中輸入導線點、設計路線等信息，設站后依次測量盾構機上2個棱鏡的坐標，同時從雙軸傾斜儀中讀取盾構機的俯仰角和扭轉角；

（3）計算偏差時，首先根據標定數據計算2個棱鏡在水平面投影的坐標，并與設計路線比較計算投影點的偏差；

（4）根據讀取的俯仰角和扭轉角對之前算出的投影點偏差進行改正，得到2個棱鏡在軸線上投影點的實際偏差；

（5）根據盾首盾尾和2個棱鏡在軸線上投影點的距離關系，由三角形相似原理計算出盾首盾尾的偏差；

（6）由2個棱鏡的實測坐標及標定時與首尾的位置關系計算出切口的里程，根據2個棱鏡在軸線上投影點的偏差計算方位角偏差。

1 數學模型

如圖1所示，O為切口中心，C為盾尾中心，P1P2為盾構機上的測量特征點，其在盾構機軸線OC上的投影點為P01和P02；P1與盾構機軸線OC組成的平面π1與通過OC的豎直平面πv之間的夾角為α1，P2與盾構機軸線OC組成的平面π2與通過OC的豎直平面πv之間的夾角為α2。α1和α2可在初始標定時求得。規定從測站看向盾構，當測量點在盾構機右側時，夾角為正值；在左側時，夾角為負值。

首先將測量特征點P1、P2投影到水平面上，得到投影點P′1、P′2的平面坐標。根據此坐標與設計軸線比較，可得到投影點P′1、P′2的相對于設計軸線的偏差I1、I2。

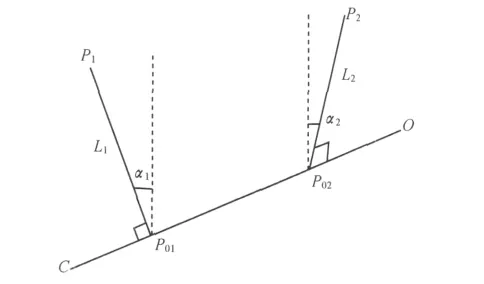
圖1 盾構機上測量特征點與盾構機軸線關系圖

如圖2，此時盾構機的轉角為α，則P01、P02的盾構轉角平面改正分別為：

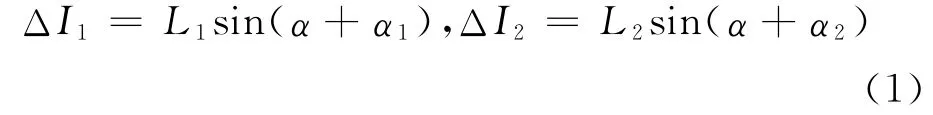
將偏差I1、I2分別加上平面改正 ΔI1、ΔI2后即得到P01、P02平面偏差 M1、M2。

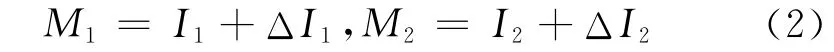
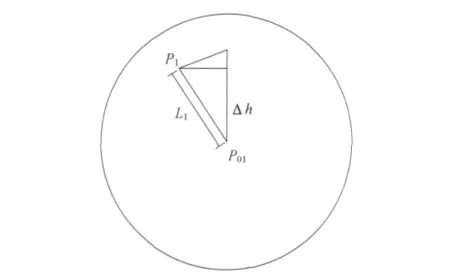
圖2 盾構機轉角改正

再根據CP01、P01P02、P02O之間距離的比例關系，利用相似三角形的原理求出盾構機切口中心、盾尾中心的平面偏差，即得到盾構實際的平面姿態。

如圖3所示，根據ΔAEF與ΔAKD相似及圖形關系可得：

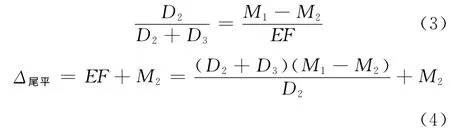
式中Δ尾平表示盾尾水平偏差。

同理根據ΔAEF與ΔGHF相似可得：

圖3 盾首盾尾水平偏差示意圖

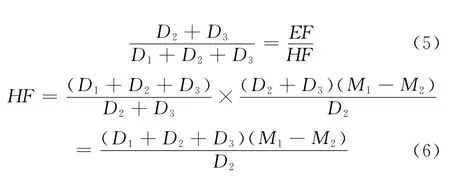
即可求得盾首水平偏差

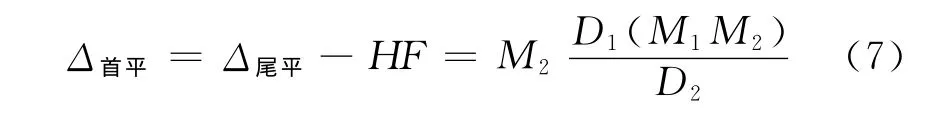
P1點的盾構轉角高程改正為：

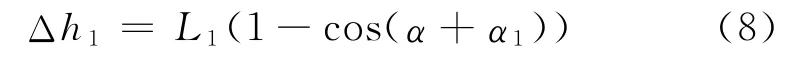
式中α為盾構扭轉角，無論左轉右轉，改正值均為正。

根據P1點的高程加上轉角引起的高程改正Δh1并歸算到盾構軸線上，得到P01點的高程，然后根據雙軸傾斜儀讀出的盾構機的當前坡度值歸算切口中心高程和盾尾中心高程，再與設計的相應里程處切口高程和盾尾高程進行比較，得到切口中心和盾尾中心的高程偏差。

2 系統開發及應用

根據上述數學模型用VC 6.0開發一套盾構自動引導系統。其程序主界面如圖4所示：界面左上方顯示盾構機的方位角、俯仰角、扭轉角偏差，以及盾首盾尾的當前里程、水平偏差、豎直偏差；右上方和右下方界面分別顯示的是盾首水平偏差和豎直偏差的歷史軌跡。左下方界面4個按鈕可以方便對全站儀和傾斜儀進行操作。該界面還可以顯示盾構機和設計路線偏差的俯視圖。

首先在始發井中盾構機上適當位置焊2個棱鏡，在工程坐標系測定2個棱鏡及盾首盾尾的三維坐標并把它們錄入“配置”下的“TBM－points”中。如圖5所示，在 “平曲線”和“豎曲線”中輸入設計曲線相關參數，以1m的間隔放樣出設計路線的三維坐標；全站儀測站坐標和后視點坐標在“導線點”中錄入。

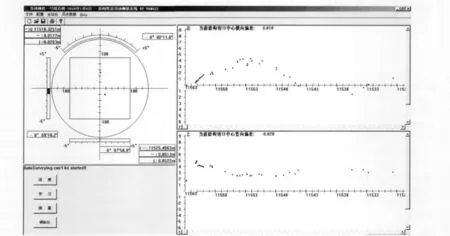
圖4 盾構自動引導系統主界面

圖5 引導系統相關配置

系統運行時，全站儀自動測量盾構機上的2個棱鏡的三維坐標并采集雙軸傾斜儀的俯仰角和扭轉角，按照上述數學模型計算出盾首和盾尾的水平和豎直偏差并實時顯示在系統界面上。

該套系統在蘇州地鐵1號線廣濟路至養育巷區間段、上海軌道交通12號線金京路至申江路區間段取得了成功的應用。所需設備主要是1臺自動全站儀、1個電子雙軸傾斜儀以及盾構機上安置的2個棱鏡，操作簡單便捷，只需盾構司機在測量時刻點擊鼠標即可。在工程應用中與人工測量方法檢核的結果說明，該方法具有較好的精度。與三棱鏡模型相比，學習測量時只需瞄準2個棱鏡，自動測量時也節省了一定的時間，也避免了由于視野夾角過小而造成三棱鏡相互混淆的情況。

3 結語

針對目前普遍使用三棱鏡模型的盾構自動引導系統，提出基于兩棱鏡模型的自動引導系統。該系統的數學模型解算過程簡單，易于程序實現。采用VC 6.0開發了相應的自動引導系統，使用過程中操作便捷，在工程中取得了成功的應用，避免了三棱鏡模型的不足，對實際施工有一定的參考價值。

［1］ 金劍鋒，王智.羅德里格矩陣在盾構引導系統中的應用研究［J］.城市軌道交通研究，2011（3）：37.

［2］ 李青岳，陳永奇.工程測量學［M］.北京：測繪出版社，1995.

［3］ 徐然.地鐵盾構智能導向系統研究［D］.上海：同濟大學測量與國土信息工程系，2008.

［4］ 陳龍飛，金其坤.工程測量［M］.上海：同濟大學出版社，1990.

［5］ 潘國榮，王穗輝.地鐵盾構施工中的若干測量手段及方法［J］.測繪通報，2001（1）：23.