淺談平面振子的阻尼運動
肖 筱 陶寅瑩 李 慶
(電子科技大學英才實驗學院 四川 成都 611731)
滕保華
(電子科技大學物理電子學院 四川 成都 610054)
大學物理中對通常的阻尼振動和平面振子已經有了很多研究[1~4],但阻尼振動的研究主要是基于一維運動,而平面振子的研究則是基于無阻尼的運動.本文將研究阻尼情況下的平面振子運動,并討論阻尼系數對其運動軌跡的影響.
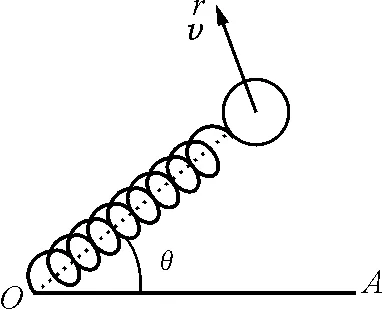
圖1 平面振子示意圖
設振子系統的一端固定在水平面上O點,另一端系一質量為m的質點, 彈簧的勁度系數和原長分別為κ和l.若質點受一阻力f=-αv(α為阻尼系數),則在極坐標下,振子的運動方程可以寫成
(1)
和
(2)
由(2)式直接得到振子系統的角動量為
(3)
這里J0是振子的初始角動量.顯然,在有阻尼情況下振子系統的角動量是隨時間t指數衰減的.于是任意時刻振子的位置可由下述微分方程和積分方程確定
(4)
(5)
利用Mathcad[5]數值計算可以得到在一定參數和初始條件下平面振子阻尼運動的軌跡,如圖2所示.圖中初始條件設置為:振子初始伸長量為1 m,初速度大小為2.45 m/s,其方向與極軸OA夾角為42.8°.可以看出,阻尼系數α為零時振子運動軌跡呈規則的花瓣狀,并且位于一個內切圓和一個外接圓之間[4].而阻尼系數α不為零時,振子的運動軌跡與上明顯不同,即阻尼系數α的大小敏感地影響振子運動軌跡的長短和形狀.隨著阻尼系數α的增大,一方面阻尼因素將導致平面振子的運動軌跡快速變短;另一方面阻尼還將使其運動軌跡的形狀明顯偏離花瓣狀,并在一定情況下有阻尼的平面振子運動軌跡會部分落入到無阻尼振子運動軌跡的內切圓中.

圖2 無阻尼和有阻尼時的平面振子軌跡,這里參數分別為:m=1,α=0.2,κ=2,l=2,J0=5(均為國際單位)
為了說明阻尼系數α不為零時平面振子運動軌跡部分落入內切圓中的軌跡特點,可以分析平面振子的徑向速度和橫向速度.在極坐標下振子的徑向速度和橫向速度分別由下式決定
利用Mathcad數值計算,可以得到與圖2相同的參數下有阻尼和無阻尼時振子徑向速度vi(t)和橫向速度vj(t),分別如圖3(a)和3(b)所示.

圖3
可以看出,無阻尼時振子的徑向速度隨時間簡諧變化,但橫向速度是平移到坐標軸上方某正數附近非簡諧的周期變化.阻尼系數α不為零時,振子的徑向速度和橫向速度都是隨時間衰減的,并且徑向速度與一維阻尼振子的速度衰減趨勢完全相似,但是此時橫向速度卻是從坐標軸上方某正數附近一直振蕩衰減到零.也就是說,此時振子橫向速度的衰減變化趨勢與無阻尼時振子橫向速度的變化趨勢大相徑庭.由此可以發現,阻尼系數α不為零時平面振子軌跡之所以部分落入無阻尼時的內切圓內,是因為其橫向速度相比無阻尼時不協調地衰減,導致平面振子所需的向心力相比無阻尼時相應減小,在彈力的作用下,最終使得平面振子在運動過程中部分落入無阻尼時的內切圓內.
綜上所述,本文通過建立平面振子在有阻尼情況下的動力學方程,利用Mathcad數值求解了一定條件下平面振子的運動軌跡,并分析了阻尼因素對其運動軌跡的影響.同時指出,有阻尼時平面振子橫向速度的迅速衰減特征是導致有阻尼時運動軌跡部分落入無阻尼時軌跡內切圓的主要原因.
參考文獻
1 周衍柏.理論力學教程.北京:高等教育出版社,1979.69
2 (美)H·戈德斯坦著.湯家鏞,陳為恂譯.經典力學.北京:科學出版社,1981.71~87
3 趙凱華.新概念物理教程·力學.北京:高等教育出版社,2004.329
4 Scheck F. Mechanics: From Newton′s Laws to Deterministic Chaos (Berlin: Springer) 2004.47~49
5 鄭桂水.Mathcad2000實用教程.北京:國防工業出版社,2000.172~176

