重復控制在衛星轉動部件動量補償中的應用

王磊，甘克力，葛升民，何平，李爽

(1.哈爾濱工業大學 控制科學與工程系，黑龍江 哈爾濱150001;2.中國空間技術研究院，北京100094)

0 引言

某些衛星的有效載荷具有轉動部件，例如光學掃描相機或掃描鏡等，這些部件的轉動引入了角動量干擾。如果干擾未經補償直接作用于衛星平臺，將會降低姿態控制系統的穩定度和指向精確度[1]。尤其對于具有撓性附件的衛星，如果轉動部件的運動為周期性往復運動，則有可能激發撓性附件的振動，使衛星姿態出現振蕩。

為減少轉動部件對衛星姿態造成的不利影響，引入一個獨立的角動量補償系統，用以直接抵消轉動部件的運動影響。選擇補償飛輪作為動量補償執行部件，為補償飛輪配置專門控制器，并在有效載荷轉動部件上安裝角度編碼器以測量轉動部件的轉動角度。控制器根據轉動部件的轉動角度計算所需要補償的角動量值，由補償飛輪輸出補償角動量，保證轉動部件與補償飛輪角動量之和接近于零，這樣就可以抵消運動部件的動量干擾。

很多控制系統都要處理周期性參考輸入或擾動信號，例如轉臺伺服系統要以一定的周期重復地操作運行[2]。重復控制基于內模原理將周期信號的動態模型植入系統的控制器內，從而實現對周期性參考輸入信號進行高精確度跟蹤或對周期性干擾信號進行有效抑制，并且這種機制在跟蹤和抑制周期信號方面都取得了一定的成就[3－4]。

在角動量補償系統工程設計中發現，跟蹤轉動部件周期運動時傳統PID控制器在高頻段有一定的相位滯后，并且轉動部件在轉速過零時存在的摩擦力矩會降低補償系統的補償精確度[5]。為保證補償效果和系統工程實用性，需要采取措施降低這些方面的影響。本文設計方案中選擇重復控制方法，在原有PID控制器中插入重復控制環節，不必調整原有控制系統參數即可大幅提高系統精確度。由于引入重復控制器使得補償系統可以最大限度抵消運動部件的力矩干擾，從而保證衛星實現高姿態穩定度、高指向精確度。本文的主要研究內容有補償系統方案設計和仿真驗證等。

1 補償系統方案設計

本節簡要介紹與角動量補償系統設計有關的基本信息，包含有效載荷運動特性與摩擦力矩特性等。

1.1 角動量補償系統

圖1為角動量補償系統示意圖，其基座安裝于衛星平臺之上，轉動部件通過轉軸和軸承與基座相連做余弦往復式掃描運動，將驅動電機的轉子固聯于轉軸之上，定子與基座相固聯。在轉軸底部安裝角度編碼器用于測量轉動部件的轉動角度位置，為補償控制器提供測量信號。

利用專門的補償飛輪在載荷運動的同時做相反方向的轉動可以抵消轉動部件的角動量干擾。補償飛輪與有效載荷具有相似的結構，同樣具有轉動部件(飛輪體)、軸系驅動電機、基座和角度測量裝置。驅動電機的轉子與飛輪體聯接，其定子則安裝在外殼基座之上。如圖1所示，將補償飛輪安裝于有效載荷基座之內，與有效載荷轉動角度測量裝置共同構成補償系統的機械結構部分。

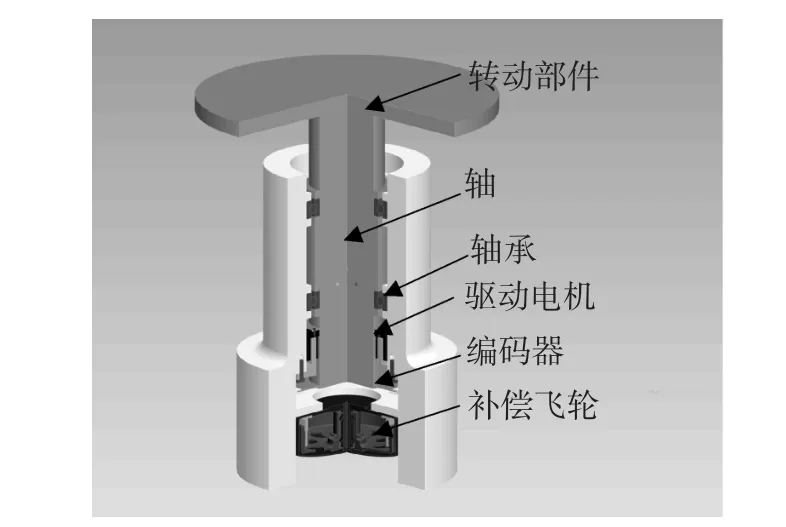
圖1 角動量補償系統Fig.1 Angular momentum compensation system

1.2 有效載荷運動規律

假設有效載荷轉動部件的運動規律為余弦掃描運動，其掃描曲線如圖2所示。轉動部件在5 s內完成12°×24°的對角線掃描，其掃描范圍為東/西12°、南/北 24°，掃描機構僅在南北方向運動，單向掃描時間為2.5 s，機械軸轉動12°。由圖2可知，余弦運動的周期 TL為5 s，將幅值換算為弧度，AL為12° × π/180°=0.209 rad。

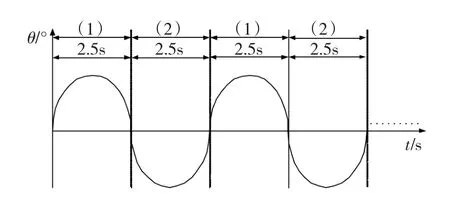
圖2 轉動部件運動規律Fig.2 Motion characteristic of rotating part

假設轉動部件南北軸角度位置測量值為θL，角加速度為 αL，則

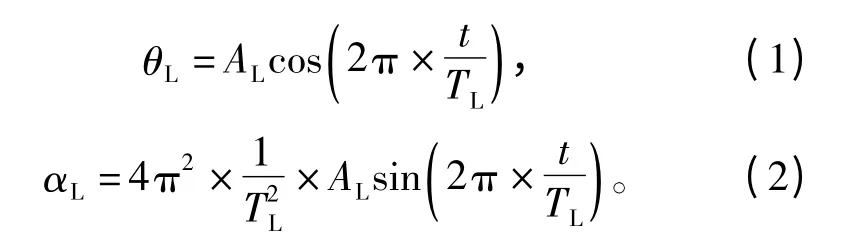
將相關參數代入式(1)和式(2)可得，最大干擾力矩為

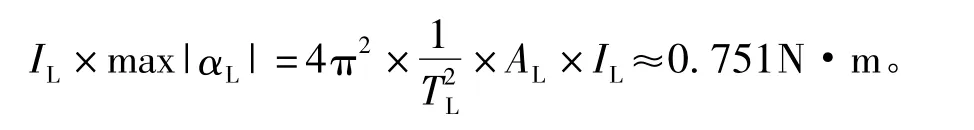
式中，IL為轉動部件的轉動慣量 2.27 kg·m2，max|·|為對變量取最大值運算。

1.3 摩擦力矩特性

有效載荷轉動部件執行機構的摩擦力矩特性如圖3所示。圖中實線部分所示為實驗可以測得的數值，由于轉速過零處的摩擦力矩信息難于測量，圖中用虛線表示。摩擦力矩在邊界潤滑和全潤滑分界處的最小值約為5 mN·m。由1.2節計算可知，該干擾為轉動部件最大干擾力矩的0.6%，轉速過零處最大靜摩擦力約為20 mN·m。

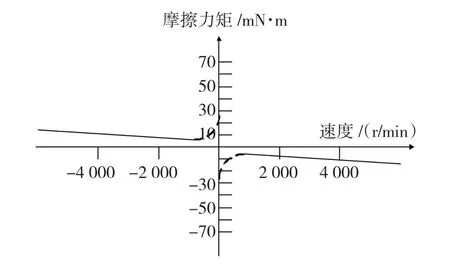
圖3 摩擦力矩特性Fig.3 Characteristic of friction torque

考慮到設計仿真過程中的數值計算問題，摩擦力矩采用 Karnopp摩擦模型[6]，并利用實驗數據進行模型參數確定。靜摩擦力矩為

式中:Tε表示外加力矩;Ts表示最大靜摩擦力矩，此處為20 mN·m，為轉動部件轉動速度。

表示Stribeck效應的非線性函數為

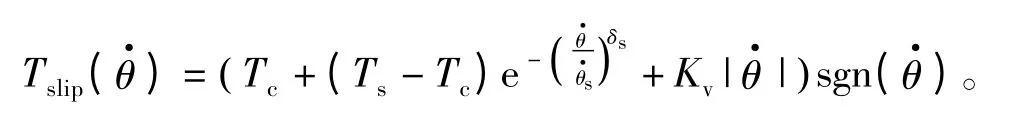
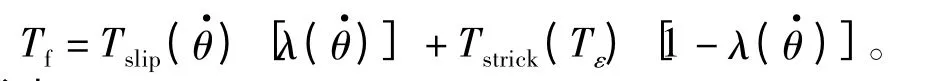
式中，

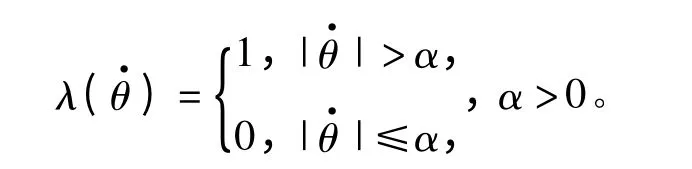
2 控制器設計

完整的角動量補償系統由有效載荷、補償飛輪、PID控制器和重復控制部分構成，其組成框圖如圖4所示。

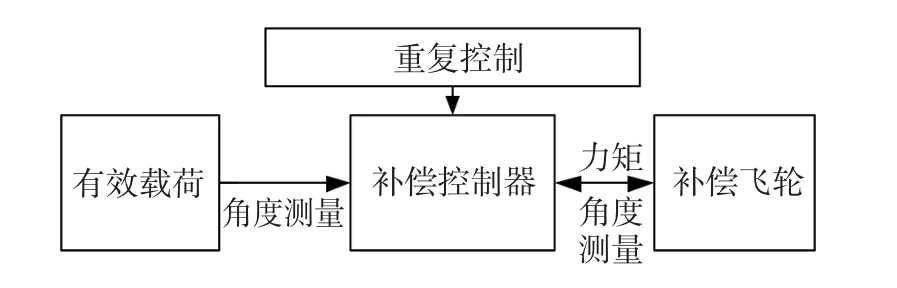
圖4 角動量補償系統Fig.4 Angular momentum compensation system

角動量補償的最終任務是要使衛星姿態穩定度和指向精確度不受有效載荷轉動部件運動的影響，所以角動量補償的本質是要求同時對轉動部件的轉動角度和轉動角速率進行補償。實際應用中對于做周期性掃描運動的有效載荷，角動量偏差中應包含兩類不同性質的成分:第一類是每個周期內角度位置的最大偏差項，該偏差在每個周期內將重復出現，出現該偏差項的主要原因為控制系統中存在的回滯與失調等因素引起的速率跟蹤誤差;另一類是角速度偏差的長期累積，該項的大小將隨時間的增加而增大，出現該偏差項是由軸承摩擦力矩的不平衡、控制電路中電位指令的不對稱性等因素引起的。由于第二類偏差的存在，僅僅跟蹤有效載荷的角速率將使殘余角動量逐漸累積，最終影響到衛星平臺的姿態指向精確度。綜上所述按如下方法構造一種雙閉環PID控制器，分別引入補償飛輪的角度位置測量信號和角速度估計信號，角速度為內環控制變量，角度位置為外環控制變量。同時，在外環角度控制器中引入重復控制算法，以有效載荷運動周期為學習周期。角動量補償系統框圖如圖5所示，其中有效載荷的干擾力矩由式(2)給出，且包含依據式(1)和Karnopp摩擦模型計算的摩擦力矩信息。

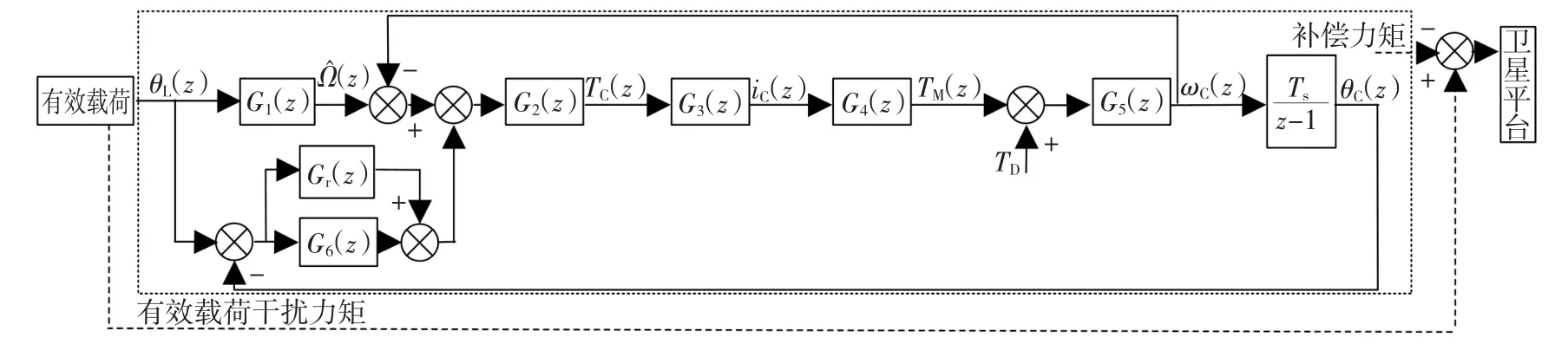
圖5 角動量補償系統框圖Fig.5 Block diagram of angular momentum compensation system

圖5 中均為變量的z變換形式，其中θL(z)是載荷轉動角度位置信號，L(z)是載荷角速度估計，TC(z)是補償飛輪力矩指令，iC(z)是補償飛輪的電機電樞電流，TM(z)是補償飛輪的電機輸出力矩，TD(z)是補償飛輪的摩擦力矩，ωC(z)是補償飛輪的轉速，θC(z)是補償飛輪的角度位置信號。

圖5中的傳遞函數及其參數均按工程整定法進行設計[7]，具體意義如下:G1(z)是為有限帶寬微分，比例系數與微分帶寬均選為40 rad/s;G2(z)是具有PID形式的補償控制傳遞函數，D項是為了提高閉環響應速度，三項系數分別為0.08、0.7、7，帶寬為90 rad/s;G3(z)是補償飛輪電樞電流閉環傳遞函數，由電路部分決定;G4(z)是補償飛輪電機的力矩系數0.25 N·m/A;G5(z)是補償飛輪控制力矩到角速度傳遞函數，IC是補償飛輪轉動慣量，為0.006 kg·m2，Ts是系統采樣時間0.01 s;G6(z)具有PI形式，主要用于清除補償飛輪長期角度偏差，比例系數選為1，積分系數為15;Gr(z)為一種插入式重復控制系統。采用這種結構的優點是，原系統控制器和重復控制器的設計相互獨立，不必對原有控制器進行任何修改而僅需要增加一個相加環節，重復控制器便可以大幅度地提高系統的穩態精確度，其數學表達式采用最常用的形式，即

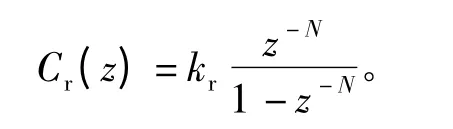
式中:N為學習周期;kr＞0用于提高系統響應快速性。

3 仿真計算

仿真用衛星本體的轉動慣量為Iy=3 000 kg·m2，在無擾動情況下，衛星平臺自身穩定度為2×10－4(°)/s，衛星姿態控制的穩定度要求優于5×10－4(°)/s(3σ)，因此允許的最大補償剩余力矩對衛星造成的穩定度擾動為3×10－4(°)/s。該衛星的姿態指向精確度要求≤0.03°(3σ)，姿態測量精確度為 3″(3σ)。補償飛輪轉動慣量為0.006 kg·m2，轉速為1 000～3 000 r/min。

為了說明加入補償系統對衛星姿態干擾的補償效果，本文對加入補償系統前后衛星的俯仰通道分別進行姿態控制仿真，同時假設衛星沒有撓性附件，仿真中衛星俯仰通道采用經典PD控制器，其中比例系數選為66，微分系數選為350。將式(1)中 θL放大倍之后，作為角動量補償系統輸入信號。

圖6所示為轉動部件以0.2 Hz的頻率做掃描運動時對衛星姿態干擾的情況。圖中沒有加入角動量補償系統，從圖中估算干擾最大值與最小值之差約為3×10－4rad，以1/2周期的變化時間來計算姿態穩定度，有

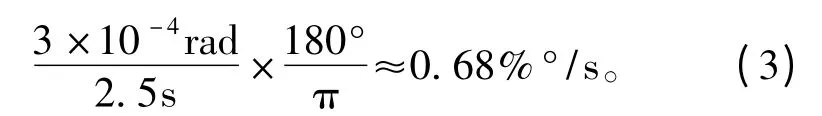
已經遠超過系統的穩定度要求。

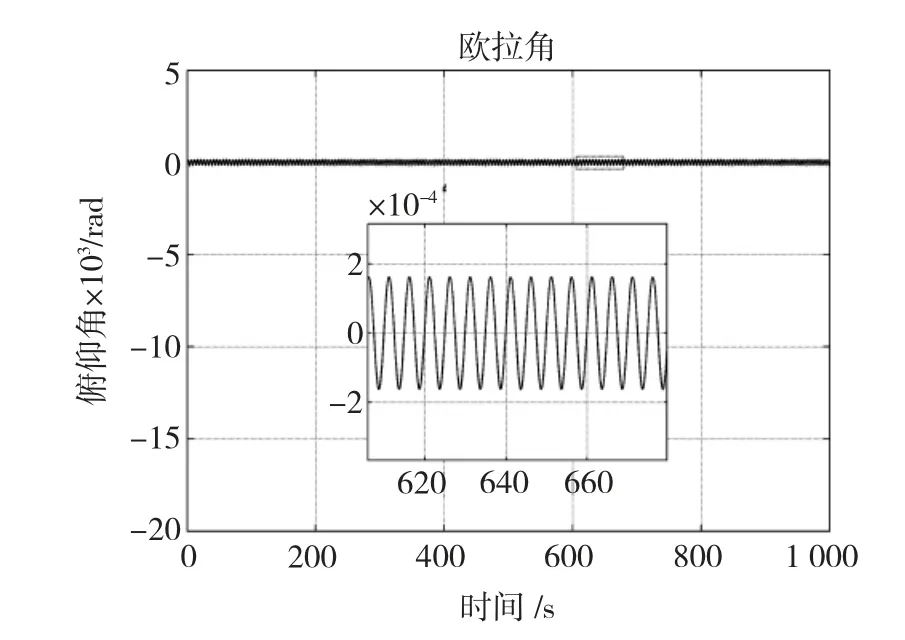
圖6 無補償時衛星姿態仿真Fig.6 Attitude simulation with no compensation

圖7 所示為加入角動量補償系統后，轉動部件仍以0.2 Hz的頻率做掃描運動，此時對衛星姿態干擾的情況。

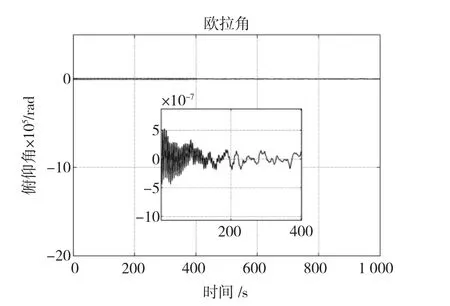
圖7 角動量補償結果Fig.7 Angular compensation result with compensation

同樣以式(3)的方法計算干擾，約為1×10－5(°)/s，達到了系統的補償要求，抵消掉角動量干擾的99%以上。

圖8所示為補償系統跟蹤有效載荷運動的角位置誤差。由圖7和圖8可以看出，重復控制器的引入有效提高了跟蹤精確度。初始角度跟蹤誤差為0.3 rad左右，在仿真時間200 s內已經基本消除了有效載荷對衛星姿態的干擾，補償系統跟蹤誤差在400 s內已經收斂，并且具有良好的穩定性。尤其指出，摩擦力矩引入的干擾在引入重復控制器后，已經被抵消掉大部分，從仿真圖中很難分辨出來。

實際工程應用中有效載荷驅動機構在速度方向改變處存在較大畸變。重復控制器在抑制該周期性擾動中，也起到關鍵作用。如果轉動部件的掃描頻率改變，可以通過有效載荷控制器在軌運行時改變學習周期參數，向補償系統發送一個頻率改變信號即可。甚至當運動為未知隨機運動時，可以關閉重復控制器，僅保留PID控制器工作。此外要說明的是，重復控制器中的kr不能選取過大，否則會使補償系統發散，本文中kr選為20。

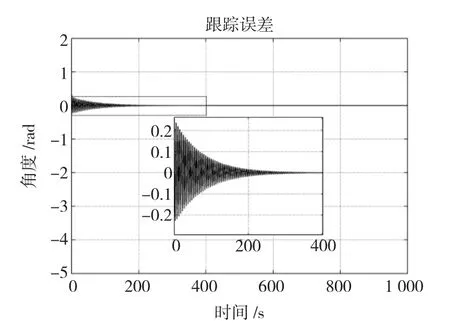
圖8 補償系統的跟蹤誤差Fig.8 Tracking error of compensation system

4 結論

本文通過一種基于插入式重復控制與經典PID控制相結合的角動量補償系統，抑制了衛星有效載荷運動所帶來的角動量干擾。仿真結果表明，相對于經典PID控制器，插入重復控制方法降低了周期跟蹤信號的跟蹤誤差，加快了收斂速度，同時對周期干擾的抑制也起到了關鍵作用，而且獨立于原有控制器的設計方法，降低了插入重復控制對原系統的影響，同時增加了系統的靈活性。

[1]CHEN Maoliang，LIU Yingying，LEI Jing，et al.On-orbit identification of disturbance torques acting on satellite with rotating payloads[C]//Proceedings of the 2009 IEEE International Conference on Mechatronics and Automation，August 9 － 12，2009，Changchun，China.2009:1342－1346.

[2]楊松，曾鳴，蘇寶庫.重復控制算法在轉臺伺服系統中的應用[J].電機與控制學報，2007，11(5):508－511.YANG Song，ZENG Ming，SU Baoku.Repetitive control algorithm in turntable servo system[J].Electric Machines and Control，2007，11(5):508 －511.

[3]Tomizuka M.Dealing with periodic disturbances in controls of mechanical systems[J].Annual Reviews in Control，2008，32:193－199.

[4]YUAN Songgui，WU Min，HE Yong，et al.Non-fragile discrete repetitive control based on two-dimension model[C]//Proceedings of the 29th Chinese Control Conference，July 29－31，2010，Beijing，China.2010:243 －247.

[5]CHEN Silu，TAN Kok Kiong，HUANG Sunan.Friction modeling and compensation of servomechanical systems with dual-relay feedback approach[J].IEEE Transactions on Control Systems Technology，2009，17(6):1295－1305.

[6]Karnopp D.Computer simulation of slip-stick friction in mechanical dynamic systems[J].Journal of Dynamic Systems，Measurement，and Control，1985，107(1):100 －103.

[7]Goodwin G C，Graebe S F，Salgado M E.Control System Design[M].New Jersey:Prentice-Hall，2001.