基于譜峭度的滾動軸承故障包絡階比跟蹤分析

劉亭偉，郭 瑜，李 斌，高 艷

（昆明理工大學 機電工程學院，昆明 650093）

旋轉機械設備的變速運行工況是一種普遍現象，機械變速運行過程中的振動信號往往包含有更為豐富的振動特征信息［1］，但該工況下的振動信號是非平穩的，一般具有幅值、頻率時變性，其振動特征通常也是時變的，因此建立在穩速運行工況下的傳統分析方法一般不易在變速運行過程中實現對故障的有效診斷，這已成為目前旋轉機械故障診斷的瓶頸［2］。同時軸承故障初始階段引起的振動通常為微弱振動信號，機械系統中大量干擾源的存在常使故障信號被湮沒在強干擾等背景噪聲中。如何在變速運行工況下對干擾進行有效抑制和在噪聲環境中對微弱故障信號進行提取是目前機械故障診斷學科中的重要研究內容之一。

包絡分析（又稱為共振解調分析）目前已被廣泛應用于滾動軸承的故障診斷，它可以有效地提取出滾動軸承故障初期的微弱沖擊信號。包絡分析中的關鍵在于濾波頻率和帶寬（共振區）的確定。傳統包絡分析方法一般是根據經驗選擇，降低了包絡分析的靈活性和準確性。近年來，基于譜峭度的包絡分析方法［3-5］被提出，它可以根據譜峭度值自適應地確定共振中心頻率和濾波頻帶，進而通過共振解調算法把微弱的沖擊振動從低頻干擾和強背景噪聲中提取出來。在近來的研究中，該方法通常是對旋轉機械穩速運行工況的振動信號，該方法是否適用于變速運行工況下的振動信號分析是一值得進一步探討的問題。在研究中發現，雖然旋轉機械軸承故障引起的微弱沖擊序列在變速運行過程中喪失了其在平穩運行下的周期性，但該沖擊序列的沖擊性本質并無改變，即持續續時間短，具有很寬的頻帶，其帶寬涵蓋了軸承及相關結構的共振頻帶并可引起相關的固有振動，因此包絡提取應同樣適合變速運行工況。但應注意的是直接對變速工況下的振動信號進行頻譜分析會造成頻率模糊現象［6］，以至于得不到故障特征，解決該問題的途徑是使用針對旋轉機械變速運行工況振動分析的階比跟蹤分析（Order Tracking Analysis）法［7］，其利用旋轉機械振動信號與轉速的階比關系，通過等角度重采樣方法將變速工況下的頻變信號轉化為階比恒定的角度域信號，對等角度信號進行頻譜分析，即可得到清晰的階比譜，進而實現對故障特征的準確提取。

本文將譜峭度分析方法和階比分析方法相結合，提出了基于譜峭度的包絡階比分析方法，用該方法成功實現了對旋轉機械變速運行工況下的滾動軸承故障特征提取。

1 基于譜峭度的包絡提取

峭度（Kurtosis）是描述波形尖峰度的一個量綱，對沖擊信號敏感，可用于評價振動信號中沖擊成分的強弱，但易受噪聲干擾而無法表征沖擊成分。近年來提出了譜峭度［4］（Spectral Kurtosis，SK）用其來反映原始信號在某個頻率成分上峭度值大小。其計算公式表示為［3-5］：

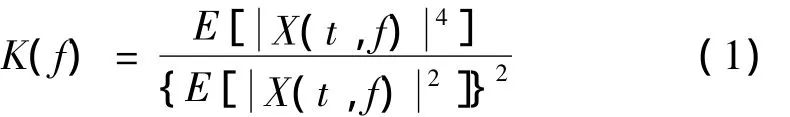
譜峭度快速計算方法采用1/3-二叉樹結構構建一系列帶通濾波器組實現譜峭度的快速計算［5］。其主要計算步驟為：

（1）獲取各級復包絡。采用與小波包分解算法相似的處理方法。首先構建兩個具有線性相位的準解析低通濾波器h0（n）和高通濾波器h1（n）：

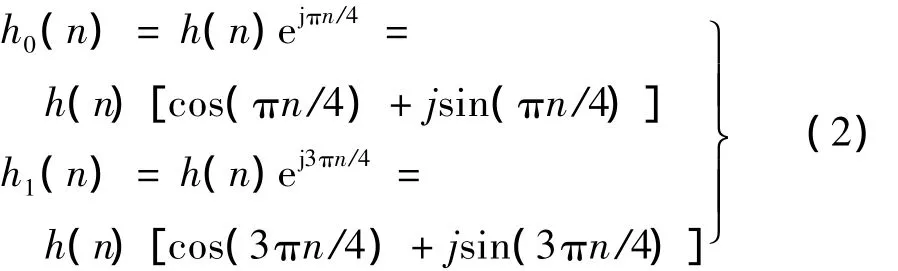
式中：h（n）為截止頻率fc=1/8+ε，ε≥0的標準低通FIR濾波器（此處為歸一化的頻率，即1代表采樣頻率fs，一般fc取 0.3［5］）；h0（n）為由h（n）頻移 1/8 后的準解析低通濾波器，其帶寬為［0，1/4］；h1（n）為由h（n）頻移3/8后的準解析高通濾波器，其帶寬為［1/4，1/2］。然后利用以上兩個濾波器h0（n）和h1（n）對原信號進行濾波，2倍降采樣，以此方式迭代，將原信號進行K級分解，把原信號分解成不同的子帶信號（n），其中系數k=0，…，K-1為分解級數，系數i=0，…，2k-1為子代信號位置索引。分解算法可用以下遞歸形式實現：

式中：當k=0時，c0（n）≡x（n）。對于子代信號（n），可以認為它是原始信號x（t）經中心頻率fi=（i+2-1）·2-k-1和帶寬Δfk=2-k-1的窄帶濾波器濾波后降采樣得到的信號［5］。由式（2）不難看出濾波器的實部相當于一個零相移濾波器，虛部相當于一個90°相移濾波器，因此分解后得到的子代信號（n）的實部和虛部相位差為90°，根據包絡檢波原理，子代信號的模即為信號的包絡（n）稱為在中心頻率fi=（i+2-1）2-k-1和帶寬Δfk=2-k-1處的復包絡信號。

為了提高分析的精度，該方法對頻帶做進一步細分，在k+1和k+2級之間插入3（2k個濾波器，和以上方法類似，通過構建三個準解析的帶通濾波器gj（n），j=0，1，2，它們的頻帶分別為［0，1/6］、［1/6，1/3］和［1/3，1/2］，對每個復包絡信號（n）進行分解，得到三個子代信號

（2）計算各復包絡信號（n）的譜峭度。根據式（1）計算復包絡信號（n）在中心頻率fi和帶寬Δfk處的譜峭度值。因此式（1）可改寫為：

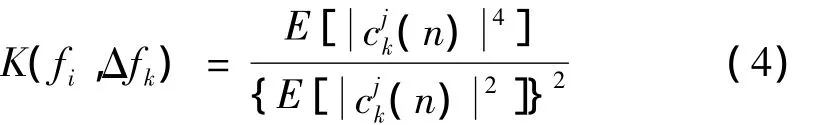
（3）獲得最佳包絡參數和最佳復包絡信號。當式（4）譜峭度達到最大時，其對應的中心頻率和帶寬即為優化包絡中心頻率fo和帶寬Δfo，其對應的復包絡即為優化復包絡信號co（n）。即：

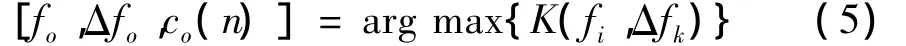
式中；argmax表示取最大值的參數，即獲得譜峭度值為最大時對應的優化中心頻率fo和帶寬Δfo，以及對應的優化復包絡信號co（n）。

2 階比分析簡介

如上所述旋轉機械變速運行工況下的振動信號為頻率時變信號，直接對其進行頻譜分析會產生所謂的頻率模糊現象［6］，為解決該問題產生了階比分析方法。階比定義為每轉的循環次數，即振動信號頻率與對應轉軸轉頻的倍數［8］，可用以下公式表示：

式中：f為振動信號的頻率；n為對應轉軸的轉速，單位為r/min，則n/60為轉頻；l為階次。

滾動軸承由內圈、外圈、滾動體和保持架四部分組成。滾動軸承故障特征頻率可由文獻［9］給出，將滾動軸承故障頻率代入公式（6）可得滾動軸承的故障特征階比，分別表示如下，

內圈故障特征階比：

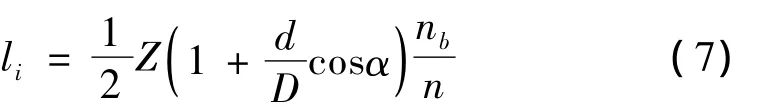
外圈故障特征階比：

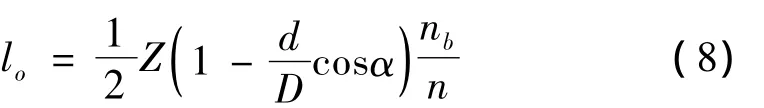
滾動體故障特征階比：

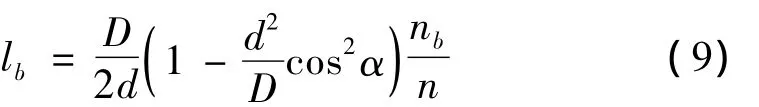
保持架故障特征階比：

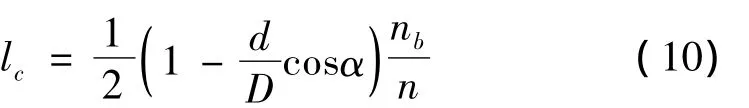
式中：Z為滾動體的個數；d為滾動體直徑；D為軸承節徑；α為接觸角；nb為軸承所在軸的轉速；n為所選取的參考軸的轉速。

階比分析根據升降速階段轉速與故障頻率的階比對應關系，把時域等時間間隔（非平穩）采樣信號通過等角度重采樣變為角度域準平穩信號。階比分析的關鍵在于如何實現等角度采樣，即階比跟蹤采樣。

研究中采用了基于轉速計脈沖的計算階比跟蹤［10-11］技術實現等角度采樣，其原理可簡述為：① 計算階比跟蹤首先對原始振動信號和鍵相信號進行常規等時間間隔同步采樣；② 利用鍵相脈沖信號進行轉速估計，并作為振動相位的參考基準，并由轉速估計得到等角度采樣的鍵相時標；③ 由得到的等角度采樣時標對原振動信號進行插值重采樣，得到振動信號的等角度采樣信號；④ 最后以等角度采樣信號為數據通過FFT實現階比譜分析，見文獻［10-11］。

3 基于譜峭度的滾動軸承包絡階比分析

基于譜峭度的滾動軸承包絡階比分析原理框圖如圖1所示，其基本分析步驟為：

（1）基于譜峭度的包絡提取：首先按式（3）對原始變速振動信號x（n）進行分解，得到不同中心頻率和帶寬下的復包絡信號（n），然后根據式（4）計算各復包絡信號的譜峭度值，最后根據式（5）得到優化的包絡中心頻率fo和帶寬Δfo，及優化的復包絡信號co（n），實現對信號包絡的自適應提取，把湮沒于強背景干擾中的微弱軸承故障振動信號提取出來。

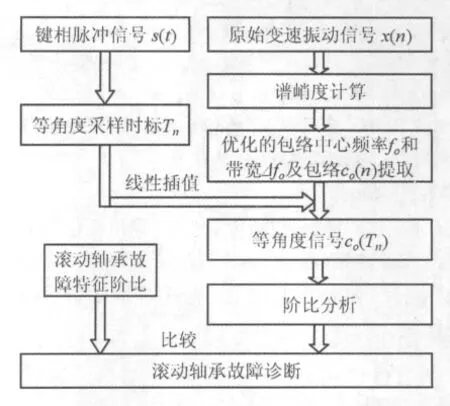
圖1 基于譜峭度的滾動軸承包絡階比分析流程圖Fig.1 The envelope order analysis flowsheet of rolling element bearing based on SK

（2）等角度采樣時標的獲取：為了實現等角度采樣必須獲得等角度采樣時標，計算階比跟蹤技術采用以下方式實現。一般情況下，在一段很小的時間間隔內可以認為轉軸角加速度恒定［11］，可用一元二次方程來描述轉角與時間的關系，即：

式中：a0、a1、a2為待定系數。把同步采集的鍵相脈沖信號s（t）連續的三個脈沖發生時刻t1、t2、t3和對應的轉角0、ΔΦ、2ΔΦ（每圈一個脈沖時取 ΔΦ=2π）代入式（11），求解a0、a1、a2，用矩陣形式可表示為：

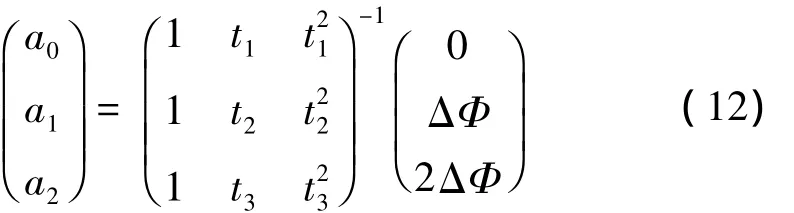
將求得的系數a0、a1、a2代入式（13）得到任意角度所對應的時刻t為：

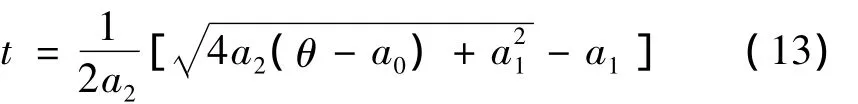
對轉角按等角度采樣間隔離散化，上式可寫為：

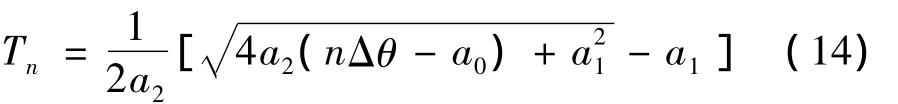
式中：Tn為第n點等角度采樣時標；Δθ為等角度采樣間隔。

（3）包絡信號等角度重采樣：等角度重采樣是根據已知的離散時域振動信號，本研究中為第1步得到的優化包絡信號co（n），在離散的等角度采樣時標Tn上插值，得到各等角度時刻的振動幅值大小，最終得到等角度信號co（Tn）。插值重采樣方法有多種，在高采樣率條件下，最簡單的線性插值即可取得較好的效果，在仿真和試驗中運用拉格朗日線性插值［12］，其公式為：

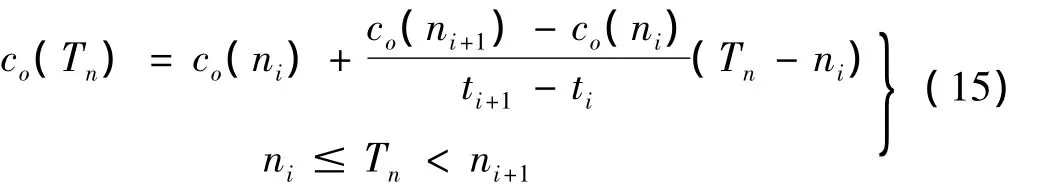
式中：ni和ni+1為離Tn最近的兩個相鄰的等時間間隔采樣時刻，co（n）為優化的包絡信號。co（Tn）即為所求的等角度采樣包絡信號。

（4）故障特征分析：對得到的等角度信號co（Tn）進行FFT得到階比譜，將其與理論計算獲得的滾動軸承故障特征階比進行對比，實現對滾動軸承故障的辯識。

4 仿真試驗分析

為了驗證本方法的有效性，進行了仿真試驗，仿真過程如下：

仿真一個固有頻率（系統固有頻率）fr=7 000 Hz幅值為0.25的單一微弱沖擊衰減振動用于仿真軸承故障的每轉內的一次沖擊：

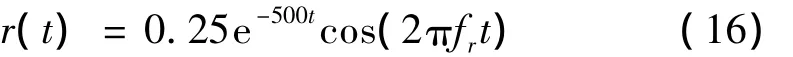
仿真一階數分別為1×、2×和3×的降速強低頻干擾：

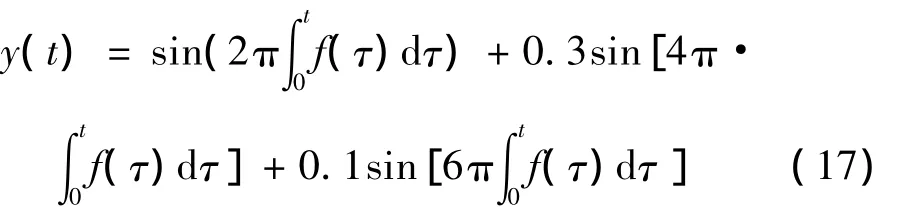
式中：f（τ）為降速過程的瞬時頻率，其起始頻率f0=25 Hz（對應起始轉速為1 500 r/min），終止頻率f1=5 Hz（對應終止轉速為300 r/min），持續時間T為4 s，并有：

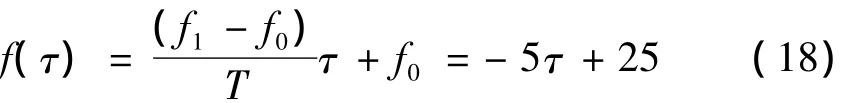
最后仿真一幅值為0.1的高斯白噪聲干擾n（t）。則仿真的軸承振動信號為：

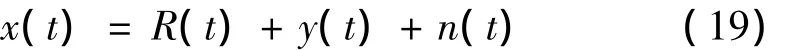
式中：R（t）為每轉重復5次r（t）的變頻（按照瞬時頻率曲線變化）仿真故障振動信號，即仿真一滾動軸承沖擊故障特征階比為5×及其諧波的沖擊信號。仿真中取采樣頻率fs=20 kHz，仿真的滾動軸承振動信號如圖2所示（圖中顯示時間從3.1～3.3 s）不難發現沖擊振動成分在整個信號中并不明顯。

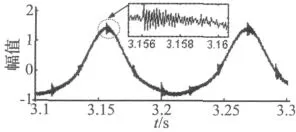
圖2 滾動軸承振動仿真信號Fig.2 Simulated vibration signal of rolling elements bearing

在沒經過基于譜峭度包絡分析，直接對原始仿真信號進行階比跟蹤得到的階比功率譜如圖3（橫坐標為階次l）所示，在圖3中只見到了仿真的強低頻干擾信號y（t）的階比，而沒有見到仿真的故障振動信號R（t）的階比。這說明故障振動信號非常微弱，被強的低頻干擾信號所淹沒。

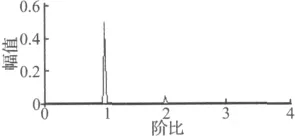
圖3 沒經過包絡分析處理的仿真信號階比譜Fig.3 Order spectrum of simulated signal without envelope analysis

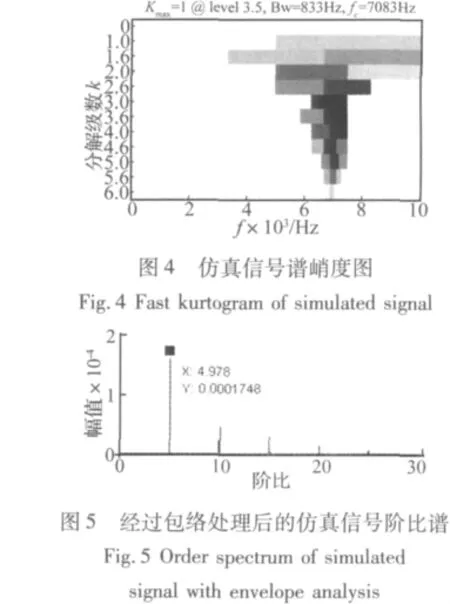
按論文介紹的方法對振動仿真信號進行分解（仿真中最大分解級數K=6），并計算在各中心頻率fi和帶寬Δfk處復包絡信號cj k（n）的譜峭度值（參見第3節步驟1），得到的譜峭度圖如圖4所示。圖4中橫坐標為頻率，縱坐標為尺度k，尺度不同帶通濾波器的中心頻率和帶寬不同，尺度越大，帶寬越窄，圖中方塊顏色深淺代表譜峭度值大小，灰度值越大譜峭度值越大。從圖中可看出在中心頻率fo為7 083 Hz，帶寬Δfo為833 Hz時譜峭度值最大，此參數即為優化的共振解調參數，這與仿真的共振頻率7 000 Hz相吻合。其對應的包絡信號即為優化包絡信號co（n），但由于其為變頻沖擊信號，故對co（n）進行計算階比跟蹤等角度重采樣（參見第3節步驟2和3）得到等角度包絡信號co（Tn），對co（Tn）進行FFT，得到的階比功率譜如圖5所示，對比圖3我們可以發現在經過譜峭度的包絡分析后，可清晰地得到仿真的5×故障特征階比及其諧波，這說明強的低頻干擾被抑制甚至被去除，微弱的故障信號被分離出來。仿真結果表明本方法的可行性。

5 測試試驗分析

研究中以ZJS50綜合設計型機械設計試驗臺為測試對象，如圖6所示。

在中間齒輪箱輸入軸位置處安裝有一故障滾動軸承，進行滾動軸承故障試驗，以外圈故障為例，試驗參數如下：故障軸承型號為N1007；安裝軸轉速從1 200 r/min（對應轉頻為20 Hz）開始降速，以降速工況的振動信號為分析對象，按式（7）計算得滾動軸承外圈故障的特征階比約為6.4×；數據采集設備為四通道NIUSB9215A采集卡；采樣頻率為20 kHz；加速度傳感器型號為4530，靈敏度為69.7 pC/g，安裝位置為軸承座；轉速脈沖測量傳感器為電渦流位移傳感器，型號為4842，靈敏度為-3.645 V/mm。圖7為采集的原始振動信號時間波形和轉速脈沖信號（注：圖中轉速脈沖信號幅值單位：V，由于要同時顯示兩個通道的信號，圖中只標出了振動信號的幅值單位）。

對測試振動信號不進行包絡分析，只進行階比跟蹤得到的階比功率譜如圖8所示，圖8中階比功率譜錯亂無章，找不到有用信息。

圖8 未經過包絡分析處理的測試數據階比功率譜Fig.8 Order pectrum of the test data without envelope analysis

對測試振動信號進行基于譜峭度的包絡提取（見第3節步驟1），得到的譜峭度圖如圖9所示，獲得的優化共振解調頻率為5 833 Hz，優化帶寬為1 666 Hz。

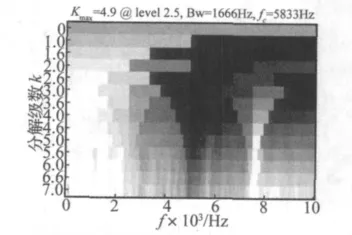
圖9 測試數據的譜峭度圖Fig.9 Fast kurtogram of the test data

按照第3節步驟2和3對提取的優化包絡時域信號進行計算階比等角度重采樣（取階比跟蹤觸發轉速為900 r/min，每轉重采樣點數為56，即最大分析階比為28×，數據長度為2 048），對應的階比功率譜如圖10所示。

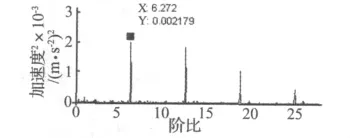
圖10 經包絡處理的測試數據階比功率譜Fig.10 Order spectrum of the test data with envelope analysis

對比圖8，從圖10中可以清晰地看到6.272×的滾動軸承外圈故障特征階比及其諧波，與滾動軸承外圈故障的理論特征階比6.4×及其諧波基本吻合（一般滾動體和內外圈之間存在1～2%轉頻的滑動［13］，以及階比譜分辨率等導致了實測故障頻率和理論故障頻率存在一定誤差）。分析結果表明本方法對實際測試有效。

6 結論

在變速工況下，由于滾動軸承故障對應的沖擊信號仍然可以激起軸承及其周圍結構的固有振動，因此共振解調方法在此同樣適用。運用基于譜峭度的包絡提取方法可以根據譜峭度值自適應的確定共振解調的優化濾波相關參數，進而把微弱的滾動軸承故障沖擊信號提取出來。階比分析可通過等角度采樣實現對旋轉機械變速運行工況的有效分析。本文將以上兩種方法相結合，實現了對變速運行工況下滾動軸承故障特征的提取。仿真和測試試驗驗證了本方法的有效性，對發展旋轉機械變速運行工況下的滾動軸承故障特征提取和診斷方法有較好的研究意義。

［1］褚福磊，彭志科，馮志鵬，等.機械故障診斷中的現代信號處理方法［M］.北京：科學出版社，2009.

［2］李志農，丁啟全，吳昭同，等.旋轉機械升降速過程的雙譜-FHMM識別方法［J］.振動工程學報，2003，16（2）：171-174.

［3］Sawalhi N，Randall R B，Endo H.The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis［J］.Mechanical Systems and Signal Processing，2007，21（6）：2616-2633.

［4］ Antoni J，Randall R B.The spectral kurtosis：application to the vibratory surveillance and diagnostics of rotating machines［J］.Mechanical Systems and Signal Processing，2006，20（2）：308-331.

［5］Antoni J.Fast computation of the kurtogram for the detection of transient faults［J］.Mechanical Systems and Signal Processing，2006，21（1）：108-124.

［6］郭 瑜，秦樹人.基于瞬時頻率估計及時頻濾波的階比分量提取［J］.中國機械工程，2003，14（17）：1506-1509.

［7］郭 瑜，秦樹人.旋轉機械非穩定信號的偽轉速跟蹤階比分析［J］.振動與沖擊，2004，23（1）：61-69.

［8］郭 瑜，秦樹人，梁玉前.時頻分析階比跟蹤技術［J］.重慶大學學報，2002，25（5）：17-21.

［9］陳 進.機械設備振動監測與故障診斷［M］.上海：上海交通大學出版社，1997.

［10］楊炯明，秦樹人，季 忠.旋轉機械階比分析技術中階比采樣實現方式的研究［J］.中國機械工程，2005，16（3）：249-253.

［11］ Fyfe K R，Munck E D S.Analysis of computed order tracking［J］.Mechanical Systems and Signal Processing，1997，13（4）：667-641.

［12］郭 瑜，秦樹人，湯寶平，等.基于瞬時頻率估計的旋轉機械階比跟蹤［J］.機械工程學報，2003，39（3）：32-36.

［13］ Sawalhi N，Randall R B.Simulating gear and bearing interactions in the presence of faults partⅠ.the combined gear bearing dynamic model and the simulation of localised bearing faults［J］. Mechanical Systems and Signal Processing，2008，22（8）：1924-1951.