兩自由度軋機(jī)非線性扭振系統(tǒng)的振動(dòng)特性及失穩(wěn)研究
侯東曉,劉 彬,時(shí)培明,劉 飛,劉云靜
(1.東北大學(xué) 秦皇島分樣自動(dòng)化工程系,秦皇島 066004;2.燕山大學(xué) 電氣工程學(xué)院,秦皇島 066004)
隨著軋制速度和軋制強(qiáng)度的不斷提高,軋機(jī)傳動(dòng)系統(tǒng)在軋制過程中時(shí)常出現(xiàn)扭振現(xiàn)象,導(dǎo)致軋制產(chǎn)品的表面質(zhì)量變差,劇烈的扭振還可能造成斷輥、斷帶等事故,嚴(yán)重威脅軋制生產(chǎn)的安全運(yùn)行。
軋機(jī)傳動(dòng)系統(tǒng)的扭振問題一直為科研人員所關(guān)注。文獻(xiàn)[1]研究了一類具有非線性摩擦阻尼的單自由度軋機(jī)扭振動(dòng)力學(xué)模型,分析了摩擦系數(shù)對系統(tǒng)自激振動(dòng)的影響。文獻(xiàn)[2]針對一類具有非線性剛度的扭振系統(tǒng)進(jìn)行了研究,采用多尺度法得到了系統(tǒng)振動(dòng)時(shí)的解析近似解。文獻(xiàn)[3]研究了具有間隙時(shí)軋機(jī)傳動(dòng)系統(tǒng)的動(dòng)力學(xué)特性,并針對間隙帶來的扭振問題提出了一些解決方法。軋機(jī)傳動(dòng)系統(tǒng)實(shí)際上是一個(gè)多非線性因素共同作用的動(dòng)力學(xué)系統(tǒng),多非線性因素的存在使得軋機(jī)的扭振行為變得更為復(fù)雜,因此研究多非線性因素的影響才能更真實(shí)反映出軋機(jī)傳動(dòng)系統(tǒng)的非線性扭振特性。
本文考慮軋機(jī)傳動(dòng)系統(tǒng)傳動(dòng)軸的非線性剛度以及軋輥受到的非線性摩擦阻尼作用,建立了軋機(jī)傳動(dòng)系統(tǒng)的兩自由度非線性扭振動(dòng)力學(xué)方程。通過坐標(biāo)變換得到電機(jī)加載力矩作用下系統(tǒng)的等效非線性扭振方程。分析了該非線性扭振系統(tǒng)在周期激勵(lì)下的主共振和分岔特性。最后以實(shí)際軋機(jī)為例,研究非線性參數(shù)對軋機(jī)主共振幅頻特性的影響以及導(dǎo)致軋機(jī)出現(xiàn)失穩(wěn)振動(dòng)的條件,為保證軋機(jī)傳動(dòng)系統(tǒng)的穩(wěn)定運(yùn)行提供了理論參考。
1 具有非線性剛度和非線性摩擦阻尼的兩自由軋機(jī)非線性扭振模型
在軋制狀態(tài)下,考慮軋機(jī)傳動(dòng)系統(tǒng)傳動(dòng)軸的非線性剛度[4]以及軋輥與軋件間非線性摩擦阻尼[1,5],可將軋機(jī)傳動(dòng)系統(tǒng)簡化為由電機(jī)和負(fù)載組成的兩自由度非線性扭振力學(xué)模型(如圖1所示)。
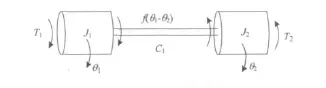
圖1 兩自由度軋機(jī)非線性扭振力學(xué)模型Fig.1 The 2 DOF nonlinear mechanical model of torsional vibration of rolling mill
圖中J1和J2分別為電機(jī)和負(fù)載的等效轉(zhuǎn)動(dòng)慣量,θ1與θ2分別為電機(jī)和負(fù)載運(yùn)轉(zhuǎn)時(shí)的扭轉(zhuǎn)角,f(θ1-θ2)=K1(θ1-θ2)+K2(θ1-θ2)3為軋機(jī)傳動(dòng)軸的非線性剛度,C為傳動(dòng)軸的結(jié)構(gòu)阻尼系數(shù),T1為電機(jī)輸入力矩,T2為負(fù)載端受到的非線性摩擦阻尼,T2=-aRPe-bRθ·2+c,其中P為軋制力,R為軋輥半徑。
由圖1中力學(xué)模型可得到如下兩自由度非線性扭振方程:
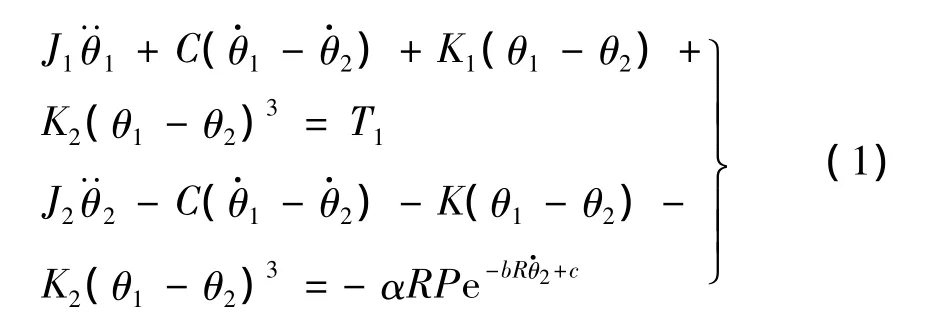
2 電機(jī)加載力矩下等效非線性扭振方程
軋機(jī)傳動(dòng)系統(tǒng)運(yùn)轉(zhuǎn)時(shí)的轉(zhuǎn)動(dòng)角是隨時(shí)間變化的,由于非線性因素的影響,軋機(jī)傳動(dòng)系統(tǒng)在零點(diǎn)附近的運(yùn)行和穩(wěn)定狀態(tài)[2,4]將與傳動(dòng)系統(tǒng)受電機(jī)加載力矩作用時(shí)實(shí)際運(yùn)行情況有較大差別[6],研究電機(jī)加載力矩作用下的軋機(jī)傳動(dòng)系統(tǒng)更接近于實(shí)際。
令電機(jī)加載力矩T1=T'1+T″1,其中T'1為電機(jī)加載力矩的恒定成分,為一常量,T″1為電機(jī)加載力矩的擾動(dòng)成分。此時(shí)電機(jī)和負(fù)載端的相對扭轉(zhuǎn)角可寫為θ1-θ2=Δθ+x1-x2,其中 Δθ為恒定加載力矩T'1造成的扭轉(zhuǎn)角,為一常量,x1和x2為擾動(dòng)力矩T″1造成的扭轉(zhuǎn)波動(dòng)角;電機(jī)和負(fù)載的轉(zhuǎn)動(dòng)速度可分別表示為,其中和分別為由力矩T'1形成的電機(jī)和負(fù)載的穩(wěn)定轉(zhuǎn)速,存在;電機(jī)和負(fù)載的轉(zhuǎn)動(dòng)加速度可分別表示為,在恒定力矩T'1下存在。將上述的代入式(1)中,并將負(fù)載端的非線性摩擦阻尼在穩(wěn)定轉(zhuǎn)速處泰勒公式展開,可得到軋機(jī)傳動(dòng)系統(tǒng)在穩(wěn)定點(diǎn)附近的等效非線性扭振方程:
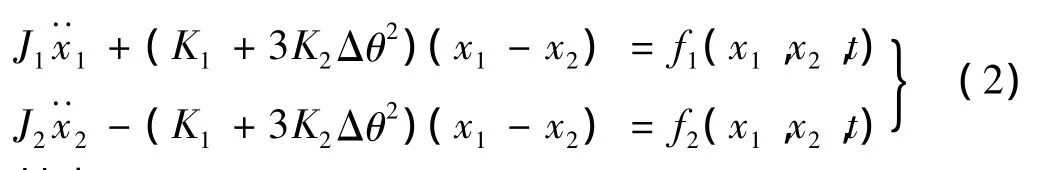
其中:
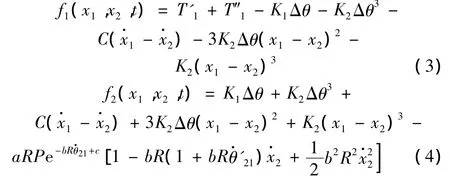
在上述非線性扭振方程中,當(dāng)系統(tǒng)的擾動(dòng)力矩趨于0時(shí),即T″1=0時(shí),存在如下的平衡力:
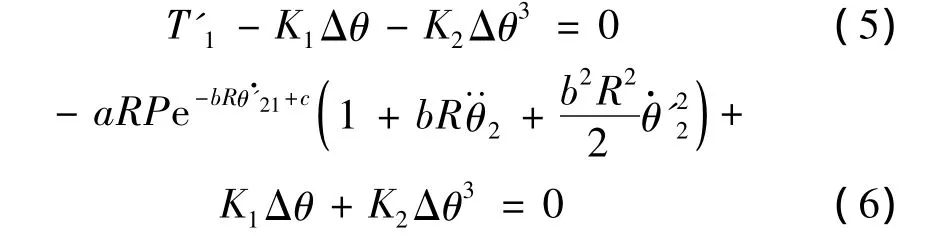
其中,Δθ和θ·21為恒定加載力矩形成的傳動(dòng)軸扭轉(zhuǎn)角和負(fù)載端轉(zhuǎn)速,為軋機(jī)傳動(dòng)系統(tǒng)運(yùn)行時(shí)的穩(wěn)定點(diǎn)。
將式(5)、式(6)代入式(2)中,考慮到式(2)中的非線性項(xiàng)為弱非線性,將其冠以小參數(shù)ε,可得到如下矩陣形式:
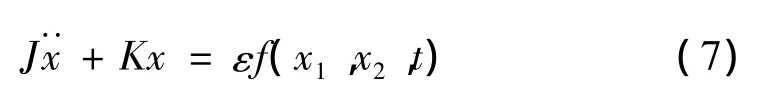
其中:
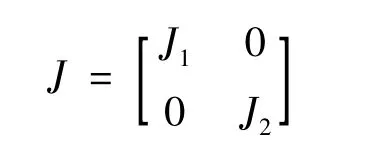
為系統(tǒng)的慣量矩陣;
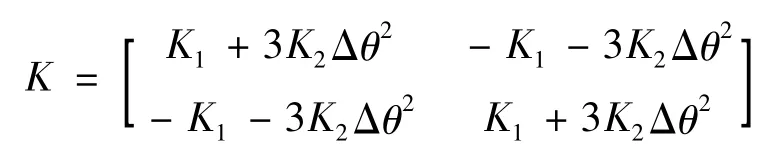
為系統(tǒng)的剛度矩陣;
f(x1,x2,t)=[f'1(x1,x2,t)f'2(x1,x2,t)]T為系統(tǒng)的非線性作用力矩陣,此時(shí):
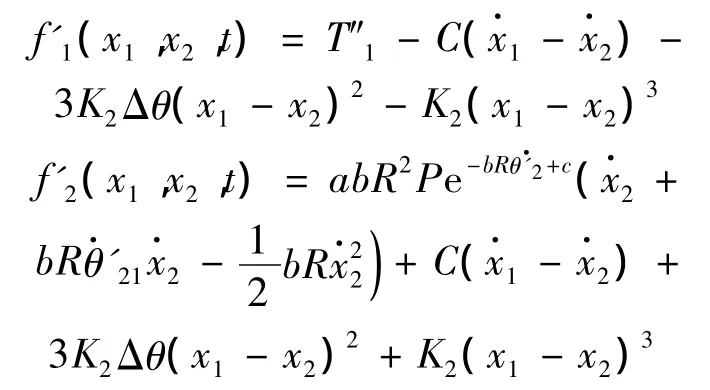
由上可見,在電機(jī)加載力矩作用下,軋機(jī)傳動(dòng)系統(tǒng)的非線性扭振方程轉(zhuǎn)換為一個(gè)同時(shí)包含二次及三次非線性項(xiàng)的方程。
3 非線性扭振系統(tǒng)的振動(dòng)特性分析
3.1 非線性扭振系統(tǒng)的主共振特性分析
由于式(7)中的兩自由度非線性扭振方程只存在一個(gè)固有頻率,因此可只考慮單頻振動(dòng)作用影響,即認(rèn)為該系統(tǒng)是以系統(tǒng)的固有頻率或某一種頻率為主的振動(dòng)[7]。
當(dāng)軋機(jī)傳動(dòng)系統(tǒng)受到外部周期激勵(lì)擾動(dòng)頻率ω接近于系統(tǒng)的固有頻率ω0時(shí),即T″1=F0sin(ωt),采用平均法設(shè)式(7)存在如下形式的周期解:
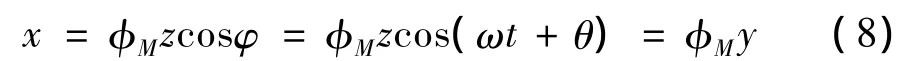
式(8)中的φM=[φM1φM2]T為振型函數(shù),可通過求解式(7)的奇次方程組得到,該奇次方程組如下:
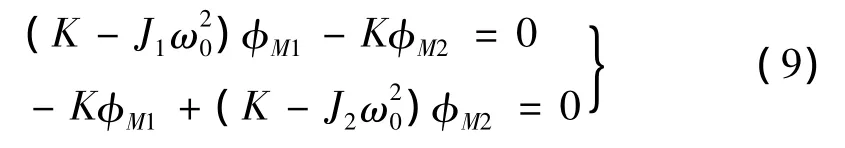
式(9)中ω0為系統(tǒng)的固有頻率,可通過求解如下特征行列式得到:

由式(10)可解得:
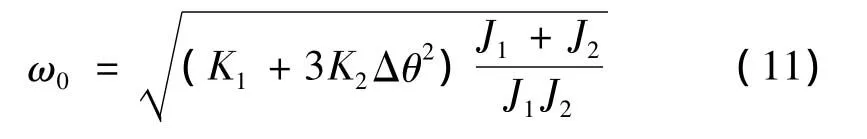
將式(11)代入式(9)可解得:

將式(7)的左邊和右邊都乘以φTM,可將式(7)化為第一主坐標(biāo)上的方程式:
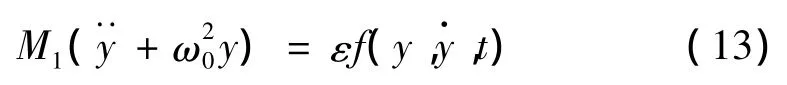
其中主質(zhì)量M1和主剛度M1ω20分別為:
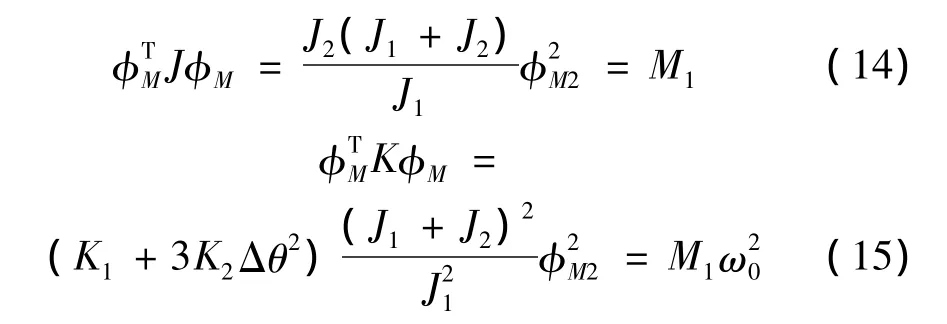
式(13)右邊的非線性項(xiàng)為:

其中:
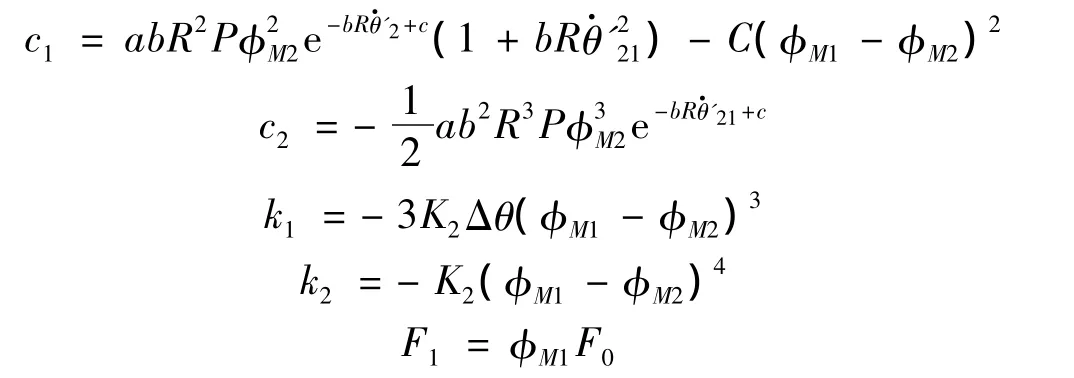
由于式(13)的方程在主坐標(biāo)上是獨(dú)立的,因此可采用單自由度系統(tǒng)的求解方法對系統(tǒng)進(jìn)行分析。
考慮到軋機(jī)傳動(dòng)系統(tǒng)受到的擾動(dòng)頻率ω接近系統(tǒng)固有頻率ω0,設(shè):

其中σ為調(diào)諧因子。
將式(17)代入式(13)可得:
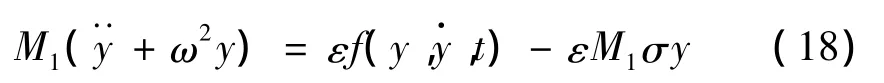
采用平均法可得到系統(tǒng)的幅值和頻率方程為:
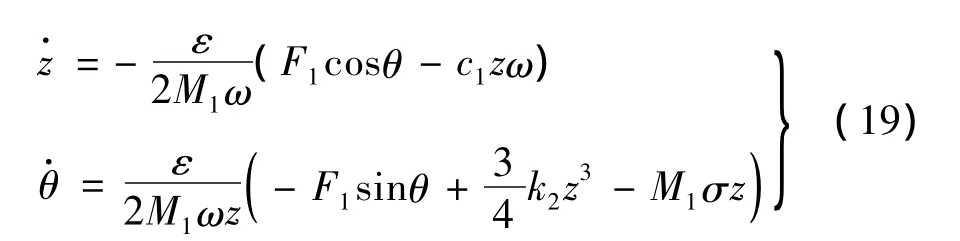
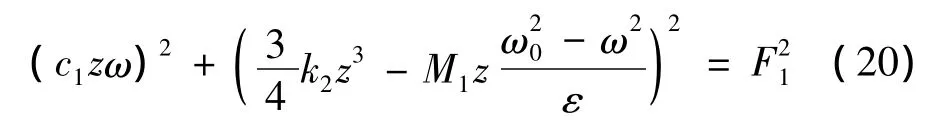
3.2 非線性扭振系統(tǒng)的分岔特性分析
為分析系統(tǒng)主共振時(shí)的分岔特性,可將式(20)考慮為奇異性理論中的一個(gè)開折問題,通過引進(jìn)附加參數(shù)來研究擾動(dòng)對方程分岔形態(tài)的影響。
將式(20)展開可得如下形式:
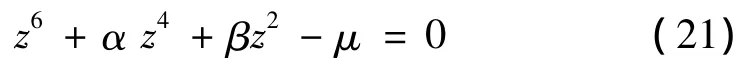
其中:
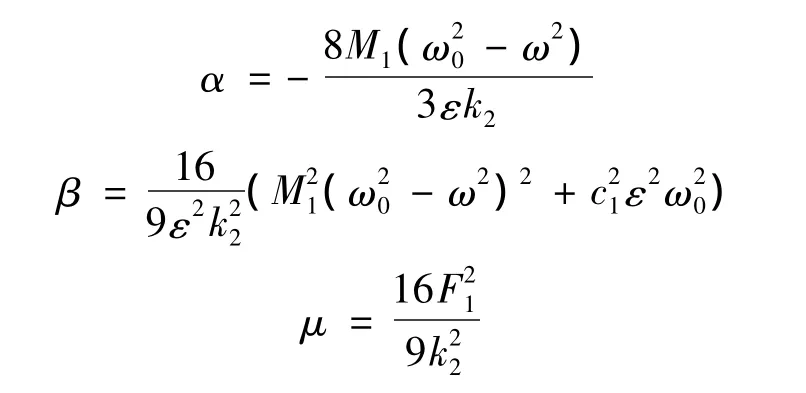
式(21)可寫為:
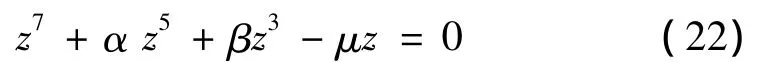
將式(22)寫成如下形式:
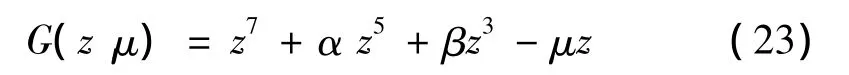
由奇異性理論可知,式(23)是范式z7-μz=0的普適開折,其余維數(shù)為2。其中,α、β為開折參數(shù),其不同的取值會(huì)導(dǎo)致系統(tǒng)出現(xiàn)不同的分岔形式;μ為分岔參數(shù),在確定的分岔形式下,振幅z將隨系統(tǒng)的參數(shù)μ的變化而發(fā)生變化。
分別將式(23)對z和μ求導(dǎo),可得到:
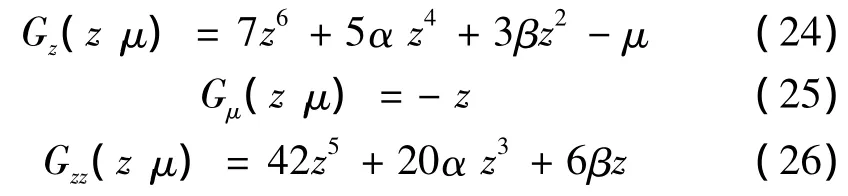
根據(jù)轉(zhuǎn)遷集的定義可得:
(1)當(dāng)G(z,μ)=Gz(z,μ)=Gμ(z,μ)=0 時(shí),存在分岔點(diǎn)集B0(Z2)=φ,B1(Z2)=φ;
(2)當(dāng)G(z,μ)=Gz(z,μ)=Gzz(z,μ)=0 時(shí),存在滯后點(diǎn)集H0(Z2)={β=0},H1(Z2)={β=α2/3,α≤0};
(3)存在雙極限點(diǎn)集D(Z2)={β=α2/4,α≤0};
(4)系統(tǒng)的轉(zhuǎn)遷集∑=B0∪B1∪H0∪H1∪D。
圖2為系統(tǒng)在不同開折參數(shù)α和β下的轉(zhuǎn)遷集。
圖3為系統(tǒng)在不同的轉(zhuǎn)遷集以及轉(zhuǎn)遷集劃分的區(qū)域中對應(yīng)的分岔曲線。

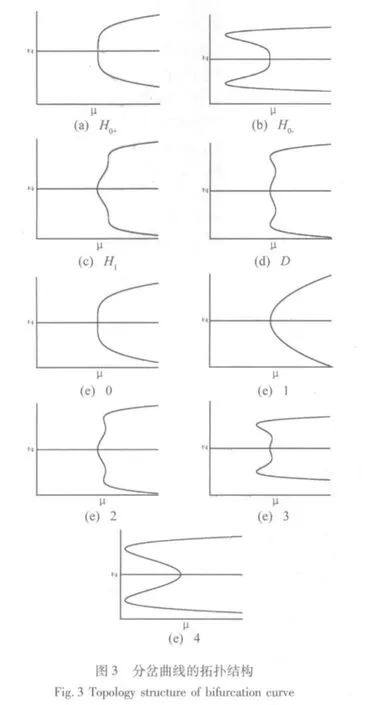
由圖3可見,系統(tǒng)具有9種不同的分岔形式,其中,H1、H0+、H0-、D為系統(tǒng)轉(zhuǎn)遷集上的分岔曲線,(e)1、(e)2、(e)3和(e)4為轉(zhuǎn)遷集劃分出的4個(gè)不同分岔區(qū)域,在這4個(gè)分岔區(qū)域中,(e)2、(e)3和(e)4都存在幅值跳躍現(xiàn)象,這對軋機(jī)的振動(dòng)是不利的,因此應(yīng)盡量使系統(tǒng)的開折參數(shù)保持在區(qū)域圖3(e)1中。
4 仿真分析
以某廠1780軋機(jī)傳動(dòng)系統(tǒng)為例,取如下參數(shù):J1=1.317 ×104kg·m2,J2=913 kg·m2,K1=1.13 × 107Nm/rad,C=1.6 × 104N/(m·s-1),R=0.42 m,a=0.1,b=0.02,c=0.5,T'1=2.15 ×106Nm,P=3.14 ×107N,φM2=1。
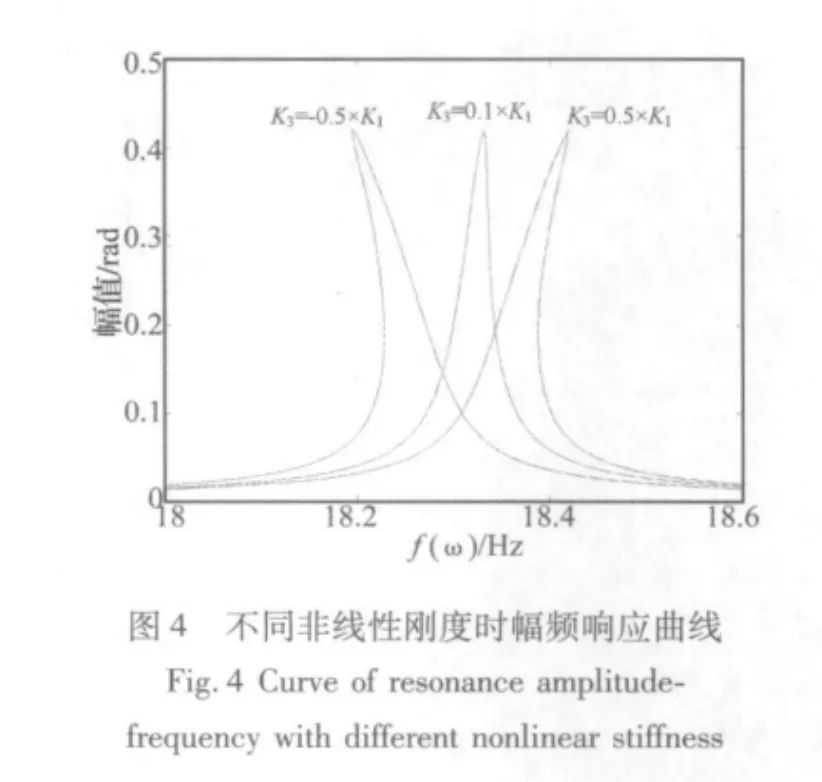
由式(20)可得到在不同非線性參數(shù)影響下系統(tǒng)的幅頻響應(yīng)變化曲線。其中圖4為不同非線性剛度下系統(tǒng)的幅頻響應(yīng)曲線,可見非線性剛度將使系統(tǒng)的幅頻曲線發(fā)生彎曲,導(dǎo)致系統(tǒng)出現(xiàn)跳躍現(xiàn)象。
圖5為取不同非線性阻尼時(shí)系統(tǒng)的幅頻響應(yīng)曲線。
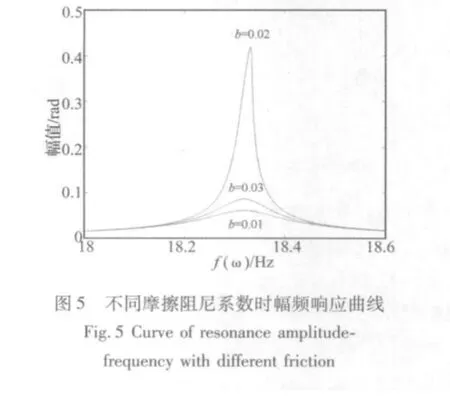
由圖5可知,非線性阻尼系數(shù)的變化會(huì)影響系統(tǒng)共振的大小,阻尼系數(shù)b值對共振的影響比較復(fù)雜,當(dāng)b在0.02附近時(shí),系統(tǒng)的等效阻尼系數(shù)c1將最小,此時(shí)系統(tǒng)的共振將最大,當(dāng)遠(yuǎn)離0.02時(shí),c1增大,正阻尼效應(yīng)變強(qiáng),共振幅值變小。
軋機(jī)阻尼系數(shù)的選取對傳動(dòng)系統(tǒng)的穩(wěn)定性有著重要作用。當(dāng)阻尼系數(shù)c1>0時(shí),軋機(jī)傳動(dòng)系統(tǒng)的阻尼為負(fù),此時(shí)將產(chǎn)生負(fù)阻尼效應(yīng),導(dǎo)致軋機(jī)發(fā)生失穩(wěn)振動(dòng)。因此當(dāng)軋機(jī)傳動(dòng)系統(tǒng)中阻尼系數(shù)c1<0,即滿足如下條件:

此時(shí)軋機(jī)傳動(dòng)系統(tǒng)是穩(wěn)定的,否則系統(tǒng)將發(fā)生發(fā)散性振動(dòng)。由式(27)可看出,傳動(dòng)系統(tǒng)電機(jī)和負(fù)載的轉(zhuǎn)動(dòng)慣量、軋輥半徑、軋制力、軋制速度、摩擦系數(shù)以及結(jié)構(gòu)阻尼系數(shù)都會(huì)影響軋機(jī)運(yùn)行的穩(wěn)定性,軋制生產(chǎn)中應(yīng)適當(dāng)選取這些參數(shù),才能避免軋機(jī)失穩(wěn)振動(dòng)的發(fā)生。
圖6和圖7為在不同的軋制速度下軋機(jī)出現(xiàn)振動(dòng)的仿真曲線。其中圖6為軋制速度等于61.6 rad/s時(shí),c1=-6.26×103N/(m·s-1)>0,此時(shí)軋機(jī)的振動(dòng)是穩(wěn)定的。
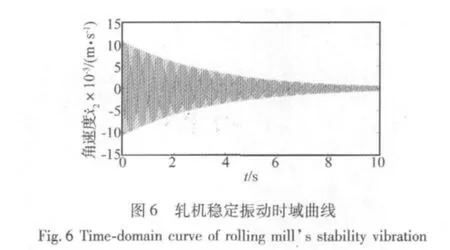
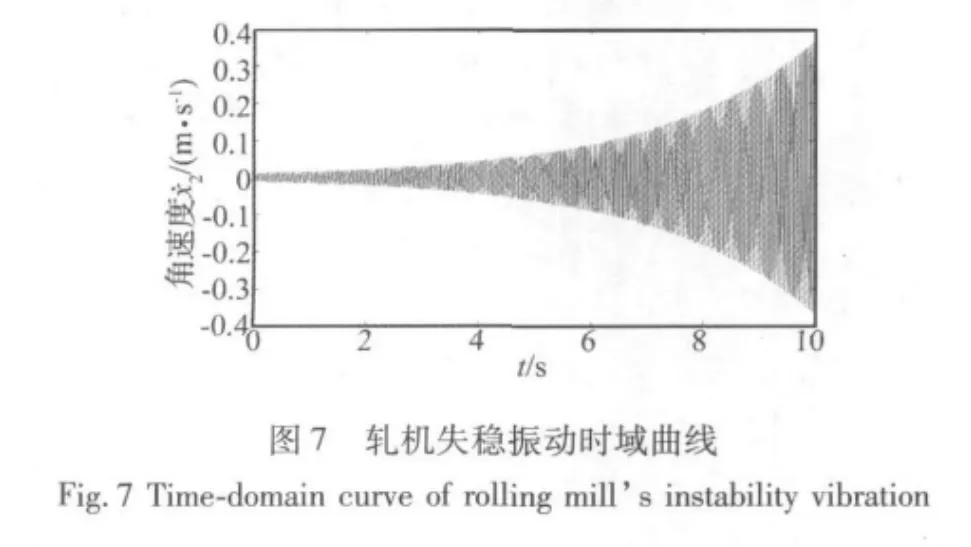
圖7中軋制速度為6.6 rad/s時(shí),c1=5.47×103N/(m·s-1)>0,此時(shí)軋機(jī)將產(chǎn)生失穩(wěn)振動(dòng),這與現(xiàn)場發(fā)生發(fā)散性振動(dòng)是比較相似的[8]。由圖7可看出,軋機(jī)發(fā)生振動(dòng)時(shí),系統(tǒng)的振動(dòng)發(fā)散,振幅隨時(shí)間增大,這將對軋制生產(chǎn)造成很大的影響,應(yīng)盡量避免這類振動(dòng)的發(fā)生。
由文中仿真可知,軋機(jī)失穩(wěn)振動(dòng)發(fā)生于軋制速度有著密切關(guān)系,這里應(yīng)注意的是文中考慮的非線性摩擦阻尼只發(fā)生在軋制過程中某一速度段(即混合摩擦狀態(tài))[8],因此對軋制工藝進(jìn)行設(shè)計(jì)時(shí),應(yīng)盡量避免軋制速度的不穩(wěn)定區(qū)域與混合摩擦狀態(tài)下速度區(qū)域重合,這樣可減少這一類不穩(wěn)定振動(dòng)的發(fā)生。
5 結(jié)論
(1)建立了具有非線線性摩擦阻尼的軋機(jī)傳動(dòng)系統(tǒng)兩自由度非線性扭振動(dòng)力學(xué)方程,并通過坐標(biāo)變換得到電機(jī)加載力矩作用下軋機(jī)傳動(dòng)系統(tǒng)的等效非線性扭振方程。
(2)得到軋機(jī)在外部周期激勵(lì)下的主共振分岔方程,應(yīng)用奇異性理論得到系統(tǒng)的轉(zhuǎn)遷集以及系統(tǒng)出現(xiàn)各種分岔行為的條件,并通過數(shù)值仿真分析了非線性剛度系數(shù)以及非線性阻尼系數(shù)對軋機(jī)主共振的影響。
(3)得到軋機(jī)發(fā)生失穩(wěn)振動(dòng)的條件,發(fā)現(xiàn)軋機(jī)傳動(dòng)系統(tǒng)中電機(jī)和負(fù)載的轉(zhuǎn)動(dòng)慣量、軋輥半徑、軋制力、軋制速度、軋輥與軋件間摩擦系數(shù)以及結(jié)構(gòu)阻尼系數(shù)等都會(huì)影響軋機(jī)運(yùn)行的穩(wěn)定性,生產(chǎn)中應(yīng)適當(dāng)選取這些參數(shù),使其滿足式(27),才能避免軋機(jī)失穩(wěn)振動(dòng)的發(fā)生,這可為抑制軋機(jī)扭振和保證軋機(jī)平穩(wěn)運(yùn)行提供理論參考。
[1]魯曉燕,葉黔元,瞿志豪.一類軋機(jī)自激振動(dòng)現(xiàn)象的分析與解決[J].上海理工大學(xué)學(xué)報(bào),2004,26(2):141-144.
[2]時(shí)培明,劉 彬.相對轉(zhuǎn)動(dòng)非線性系統(tǒng)及其在強(qiáng)迫激勵(lì)下的解[J].物理學(xué)報(bào),2007,56(7):3678-3682.
[3] Wang Z H,Wang D J.Dynamic characteristics of a rolling mill drive system with backlash in rolling slippage[J].Journal of Materials Processing Technology,2000,97(1):69-73.
[4] El-Bassiouny A F.Vibration and chaos control of nonlinear torsional vibrating systems[J].Physica A,2006,366(1):167-186.
[5] Niziol J,Swiatoniowski A.Numerical analysis of the vertical vibrations of rolling mills and their negative effect on the sheet quality[J].Journal of Materials Processing Technology,2005,162(15):546-550.
[6]劉浩然,張業(yè)寬,李曉梅,等.軋機(jī)非線性傳動(dòng)系統(tǒng)沖擊扭振的研究與抑制[J].振動(dòng)與沖擊,2010,29(7):179-183.
[7]鄭兆昌.關(guān)于線性和非線性系統(tǒng)內(nèi)在的本質(zhì)聯(lián)系——多自由度非線性系統(tǒng)的定性與定量分析[J].振動(dòng)與沖擊,2008,21(1):4-8.
[8]鄒家祥,徐樂江.冷連軋機(jī)系統(tǒng)振動(dòng)控制[M].北京:冶金工業(yè)出版社,1998:75-95.

