基于小波變換和反向傳播網絡的模態參數辨識

代 煜，張建勛

(南開大學 機器人與信息自動化研究所，天津 300071)

小波變換是一種能對觀測信號進行時頻聯合分析的方法，系統的自由衰減響應信號在連續小波變換域上的系數分布呈現出脊的特征，由此發展出多種根據脊上小波變換系數的相位、幅值信息使系統自動解耦，并提取線性系統的模態參數［1-3］或弱非線性阻尼及剛度［4］的方法。

在對系統的自由衰減響應信號進行小波變換時，小波變換系數必然會受到邊界效應的影響。邊界效應產生的根本原因是小波變換中的卷積運算，實際采集的信號都是在時域離散而且有限長的，對這樣的序列作卷積相當于加矩形窗，因此在小波變換系數的兩個邊界處會發生畸變，這必然影響到模態參數的識別。對于模態參數識別中遇到的邊界效應問題，目前主要有以下幾種解決方案:Boltezar和Slavic［5］提出用反射窗法、等窗面積法和自適應小波函數法來改變小波函數以消除邊界效應;伊廷華等［6］提出運用自回歸滑動平均模型進行信號預測以消除邊界效應的影響;徐增丙等［7］提出運用最小二乘支持向量機對小波骨架進行預測延拓的方法;Kijewski和Kareem［8］提出采用鏡像延拓技術以消除邊界效應對小波變換系數的影響;Yan等［9］定量計算了不受邊界效應影響的小波變換系數的范圍，指出只有這部分系數才能用于估計模態參數，其余受到邊界效應影響的部分應當剔除。這幾種方法可以分為兩類:一類是通過調節小波函數中的參數實現對邊界效應的抑制，一類是對信號進行延拓以獲得較多不受邊界效應影響的小波變換系數。受到種種條件的限制，小波函數的改變程度有限，因此研究信號的延拓方法是克服邊界效應的最重要途徑。在眾多的延拓方法中，類似鏡像法、補零法的一些方法不具有對待分析信號的自適應性，這將對模態參數的估計精度帶來一定程度的影響。

考慮到人工神經網絡具有通過自學習逼近任意映射的能力，突破了需要建立參數模型的傳統方法，本文將利用反向傳播網絡對采樣時長較短的自由衰減響應信號進行雙向延拓，然后對信號進行連續小波變換，從而提取各階模態的阻尼比和無阻尼自振頻率。

1 基于連續小波變換的模態參數識別方法的理論基礎

小波變換是一種能對信號進行多尺度(分辨率)分析的線性變換。設ψ(t)是L2(R)(L2(R)表示平方可積的函數空間)內的實值或復值函數，當且僅當ψ(t)的傅里葉變換ψ^(ω)滿足以下不等式時函數ψ(t)可以成為母小波:

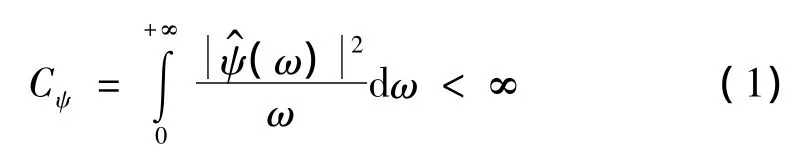
函數x(t)∈L2(R)在尺度因子為a，時移因子為b時的連續小波變換Wx(a，b)表示為:

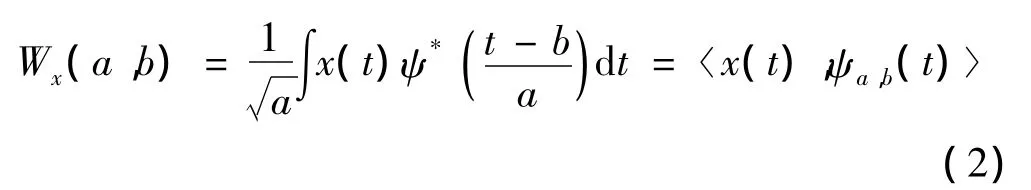
式中，a，b和t均是連續變量，且a＞0，ψ*(·)表示復共軛，〈·〉表示卷積。本文采用最常用的Morlet復小波作為母小波，定義如下式所示:

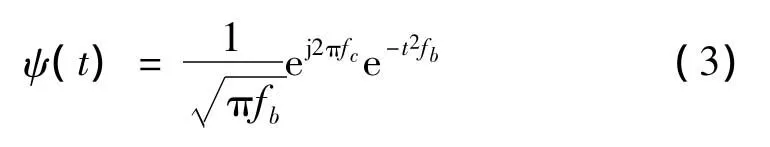
式中fc為小波中心頻率，fb為帶寬參數，j是虛數單位。二者都可因分析對象的不同而改變，這就提供了極大的靈活性。

線性多自由度系統的自由衰減響應為［9］:

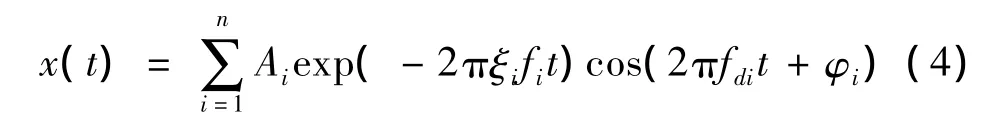
式中Ai表示第i階模態的振幅，φi表示初相角，fi是第i階模態的無阻尼自然頻率是有阻尼自然頻率，ξi表示阻尼比，n表示模態的階數。根據漸進信號的相關理論［10］，x(t)的Morlet小波變換系數的近似表達式為:

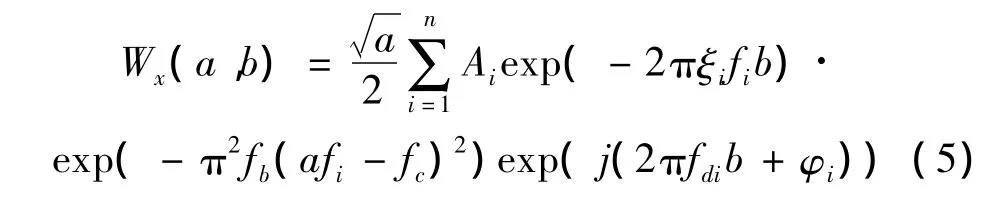
由式(5)可見，對于每一個時移因子b，在尺度ai=取得局部極大值，因此可以提取到小波脊，并且認為在這個尺度下僅有第i階模態的響應決定著小波變換系數，其余(n-1)個模態的影響可以忽略不計，此時多模態被解耦。因此，尺度為ai時的小波變換系數可以表示為［9］:

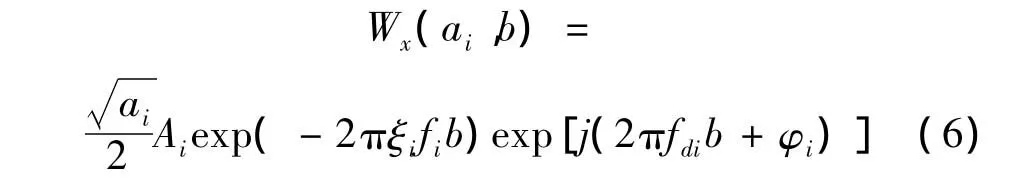
小波變換系數的模和輻角可表示為［9］:

對式(7)和式(8)應用對數和微分運算，第i階模態的無阻尼自然頻率fi和阻尼比ξi由下式估計［9］:

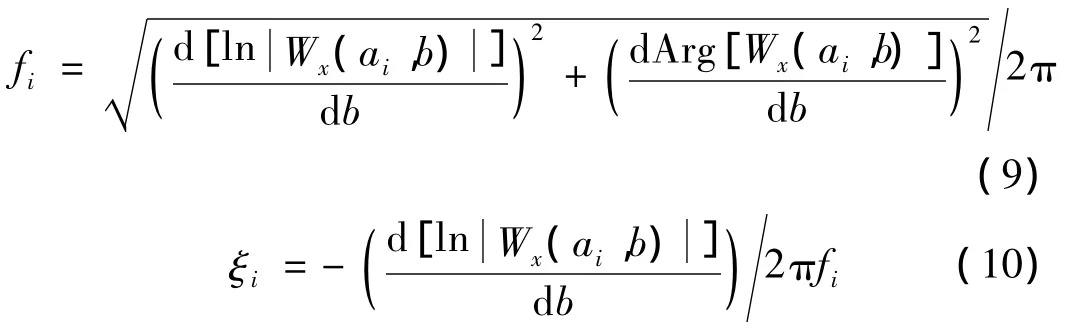
式中ln［·］表示取自然對數，Arg［·］表示求輻角。

為了分離信號中兩個較接近的頻率成份fi和fi+1，可以通過改變fb和fc提高頻率分辨率，但同時時間分辨率會下降，時間分辨率下降帶來的后果是邊界效應更加嚴重。Yan等［9］研究了時頻分辨率對模態解耦和邊界效應的影響，計算了小波參數的選擇范圍，如式(11)所示:

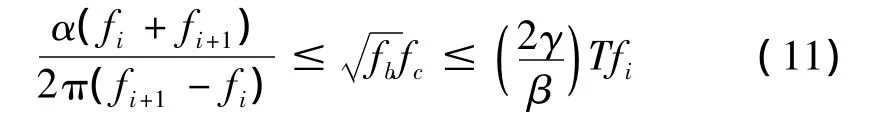
式中，α、β和γ均是用于調節范圍的常數:α=2、β=4和γ=0.4;T表示自由衰減響應信號的采樣時長。此外，為滿足小波函數的容許性條件，還應當使。Yan 等［9］還給出了邊界效應的影響范圍:

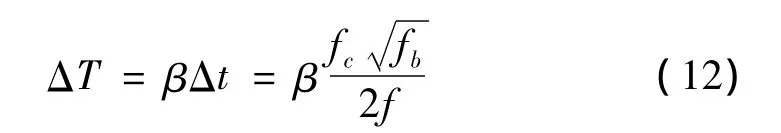
式中，f表示小波分析窗的中心頻率。值得注意的是，當待分析信號的采樣時長較短或者模態較密集時，式(11)將會無解，因此必須考慮增加信號的采樣時長。

2 利用反向傳播網絡對信號的雙向延拓

利用反向傳播神經網絡對自由衰減響應信號的延拓建立在一定數量的信號樣本之上。神經網絡的實質就是依據已有的樣本數據，通過訓練獲得并存儲樣本所隱含的特征關系，因此它具有很強的學習適應能力。

本文提出的用于信號延拓的三層反向傳播網絡模型如圖1所示，由輸入層，隱藏層和輸出層組成，同層神經元間無聯系，前后層間全連接。圖1中輸入層樣本的個數p表示前p個信號的離散采樣點對下一個采樣點有直接影響，而最新觀測值將比早期觀測值包含更多信息。網絡中隱藏層的傳遞函數都采用S型正切函數:

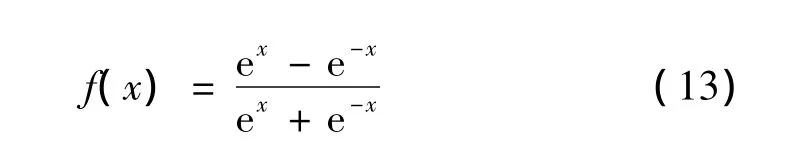
輸出層用線性傳遞函數。對于在0到T時刻等時間采樣的信號序列{x(1)，x(2)，…，x(q)}，利用反向傳播網絡對信號進行雙向延拓的步驟如下:

(1)離散時間序列的歸一化處理。為了避免神經網絡的不穩定性及收斂速度慢等問題，必須先對原始數據進行歸一化處理。本文通過式(14)將原序列變換到［0，1］區間:

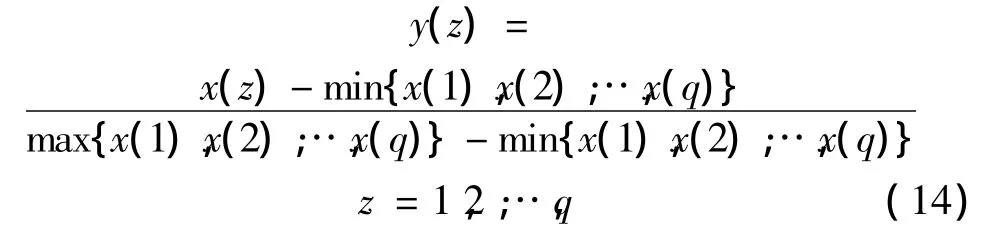
式中，max{·}和min{·}分別表示求序列的最大值和最小值。

表1 反向傳播網絡的訓練樣本(1)Tab.1 Training samples of back propagation network(1)

表2 反向傳播網絡的訓練樣本(2)Tab.2 Training samples of back propagation network(2)

(2)對反向傳播網絡的訓練。從上一步驟得到的序列{y(1)，y(2)，…，y(q)}中獲取訓練樣本，如表1和表2所示，表1中的p個訓練樣本用于預測在T時刻之后的信號序列，而表2中的p個訓練樣本用于預測在0時刻之前的信號序列。訓練樣本由輸入層經隱藏層傳遞到輸出層，輸出層將訓練結果與期望值進行比較，按照減少誤差的方向，從輸出層反向經隱藏層修正各連接權值，最后回到輸入層，這個過程反復進行，直到反向傳播網絡的輸出誤差小于設定值時才認為訓練完成。

(3)對信號序列的雙向延拓。為預測T時刻之后的h點信號序列，對上一步驟中訓練完的網絡依次輸入{y(q-p+1)，y(q-p+2)，…，y(q)}，{y(q-p+2)，y(q-p+3)，…，y(q+1)}，…，{y(q-p+h)，y(q-p+h+1)，…，y(q+h-1)};為了預測0時刻之前的h點信號序列，對上一步驟中獲得的另一個反向傳播網絡依次輸入{y(p)，y(p-1)，…，y(1)}，{y(p-1)，y(p-2)，…，y(0)}，…，{y(p-h+1)，y(p-h)，…，y(2-h)}。雙向延拓的好處在于，它能夠使得原始信號序列的小波變換系數不受邊界效應的影響，而受到邊界效應影響的小波變換系數均來自于對延拓信號序列的連續小波變換，這就能夠使得原始信號的小波變換系數對最終模態參數識別結果的貢獻最大。

(4)通過式(15)將神經網絡輸出序列的幅度還原:

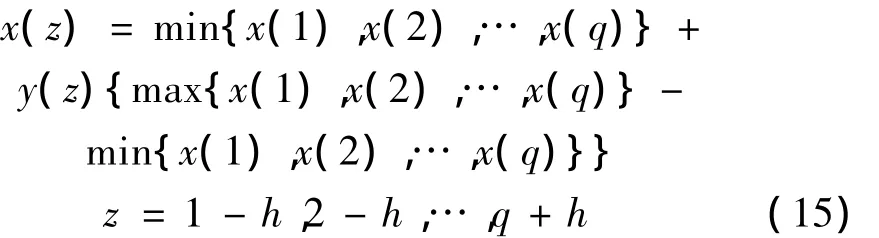
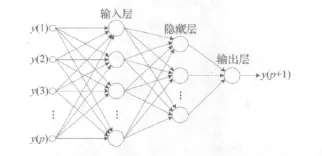
圖1 用于信號雙向延拓的反向傳播網絡Fig.1 Back propagation network developed for signal extension in both directions

3 數值仿真

兩自由度有阻尼系統的自由衰減響應如式(4)所示，令式中i=2;f1=10 Hz;ξ1=0.005;φ1=π/6;f2=12 Hz;ξ2=0.01;φ2= π/4;Ai=1(i=1，2);采樣頻率fs=200 Hz以及采樣時長T=1.5 s。將這些數據代入式(11)，無解。對于圖1所示的反向傳播網絡，輸入層的神經元個數設為40，隱藏層的神經元個數為5，利用表1和表2中的樣本對神經網絡進行訓練，取p=200。初始學習速率參數設置為0.05，動量系數設為 0.9，目標誤差設為 1 ×10-4［11］。圖 2 給出了利用反向傳播網絡對信號進行雙向延拓的結果(延拓序列的長度h=100)，圖中兩條豎線間的區域是原始信號，實線是延拓的信號，虛線表示該自由衰減響應信號的理論幅值。從圖2中可見只是在信號幅度的突變處延拓的信號與其理論值有少量差異，其余時刻二條曲線基本吻合。將信號的采樣時長改為2.5 s，代入式(11)解得3.5≤≤5。根據式(12)計算得到邊界效應的影響范圍，將這部分受到邊界效應影響的小波變換系數剔除，而后利用式(9)和式(10)辨識各階模態的阻尼比和無阻尼自振頻率。

考慮到實際采集的自由衰減響應信號常常被噪聲污染，表3給出了不同噪聲水平下模態參數識別的相對誤差，所加的噪聲為零均值的高斯噪聲。信號的噪聲水平由信噪比(SNR)來衡量，SNR定義為信號標準差與噪聲標準差的比值［12］。設r表示某個量的精確值，r0表示它的測量值或者估計值，相對誤差定義為:

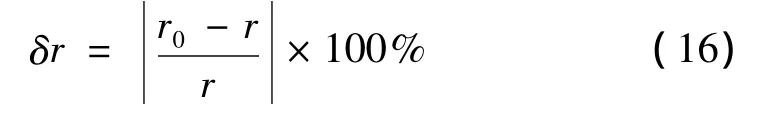
從表3可見，基于反向傳播網絡的雙向延拓方法削弱了邊界效應對模態參數識別的影響，這種方法對于信號采樣時長較短或者模態較密集的場合有效。值得注意的是，由于在信號幅度的突變處延拓信號的質量較差，這給阻尼比的估計帶來一定影響。從提取模態參數消耗的時間來看，SNR越低，訓練神經網絡所需要的時間越長。

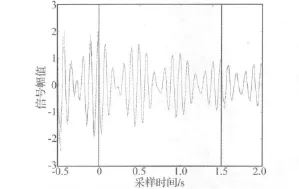
圖2 利用反向傳播網絡對自由衰減響應信號的延拓Fig.2 Extension of free decay response signal using back propagation network

如果僅采用基于連續小波變換的模態參數識別方法，由于不能計算得到合適的，也就是邊界效應將影響到所有的小波變換系數，這將導致模態參數識別結果的完全錯誤。如果采用直接設計神經網絡辨識模態參數的方法，就必須要求一定數量的訓練樣本，如果訓練樣本的SNR和待辨識信號的SNR差距較大就不能得到較好的辨識結果，而小波變換能夠在一定程度上克服噪聲的影響，這就避免了單純使用基于神經網絡的辨識方法帶來的不確定性。

4 實際問題的仿真分析

本文提出的模態參數識別方法在對用于微創外科手術機器人的力傳感器的動態性能測試實驗中得到了應用。具備力感知功能的四自由度微創外科手術機器手如圖3所示，機器手通過右端的快換接口安裝在微創外科手術機器人的機械臂末端，機械手中部是外徑10 mm，長約500 mm的空心金屬圓桿，手術開始時機器手經開在患者腹腔上的通道插入體內，由機器手左端鉗形工具夾持手術針或其他器械完成整個手術。為了測量手術過程中鉗形工具與患者內臟組織的接觸力，將應變片陣列布置在圓桿表面上靠近鉗形工具的位置，并對圓桿進行了必要的切削加工以滿足應力集中和輸入輸出引線的需要。

表3 不同信噪比下模態參數識別的相對誤差(fb=4，fc=2)Tab.3 Relative errors of identified modal parameters with different SNR(fb=4，fc=2)

力傳感器的動態性能測試采用如下方法:將粘貼了應變片陣列的圓桿一端裝夾在傳感器的標定裝置上，此時的圓桿可視為一個變截面懸臂梁，圓桿的另一端拴一根細銅絲，細銅絲繞過安裝在標定裝置上的滑輪吊起砝碼，通過剪斷銅絲，突然釋放砝碼，使得圓桿做彎曲自由振動，采集應變信號并從中提取各階應變模態的無阻尼自振頻率和阻尼比。由于應變信號很微弱且易被噪聲污染，經過調理(包括調零、約3萬倍的放大和截止頻率為318 Hz的低通濾波)之后僅能獲得0.15 s的自由衰減響應信號(如圖4所示)，信號的采樣頻率為2 000 Hz。由于信號的采樣時長過短，不能直接使用基于連續小波變換的模態參數識別方法。

圖3 具備力感知功能的微創外科手術機器手Fig.3 Minimally invasive surgery manipulator with force sensing ability

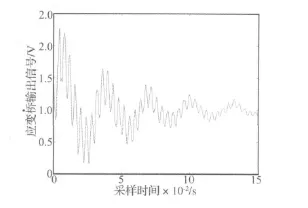
圖4 調理后的應變橋輸出信號Fig.4 Output of strain gauge bridge after signal conditioning

表4給出了對信號雙向延拓后，應用連續小波變換對力傳感器的應變模態參數進行辨識的結果(所用的反向傳播神經網絡如圖1所示，參數與第3節數值仿真中所用的參數相同)，由于低通濾波器的限制，僅能辨識到前兩階應變模態。表4給出的辨識結果表征了力傳感器的動態特性，為傳感器的建模以及進一步設計補償器提高傳感器的動態響應速度提供了實驗依據。當阻尼比較大時，自由衰減響應信號的衰減速度很快，而在實際信號中所包含噪聲的幅度卻不會以同樣的規律衰減，這就導致有用信號逐漸被噪聲淹沒，本文提出的方法為這樣一類問題提供了解決方案:將這部分受噪聲污染較重的信號直接剔除，而后對信號進行雙向延拓，延拓的信號比原信號具有較高的信噪比，從而能夠更加準確地利用基于小波變換的方法估計模態參數。

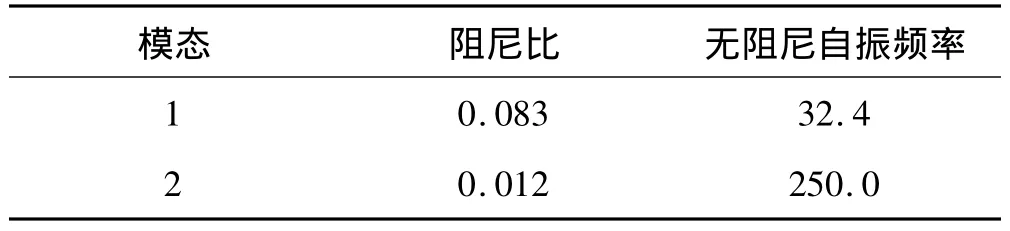
表4 力傳感器應變模態參數的辨識結果(fb=1，fc=2)Tab.4 Identified strain modal parameters of force sensor(fb=1，fc=2)

5 結論

考慮到人工神經網絡具有自學習和自適應的能力，本文提出了一種基于連續小波變換和反向傳播神經網絡的模態參數辨識方法。利用反向傳播神經網絡對自由衰減響應信號的雙向延拓，解決了小波變換的邊界效應問題，擴展了傳統模態參數辨識方法的應用領域。數值仿真以及對力傳感器進行的動態特性測試實驗表明，本文提出的方法在信號的采樣時長很短時也能夠準確地辨識各階模態的阻尼比和無阻尼自振頻率，實用性較強，并體現出一定的抗噪聲能力。

［1］ Le T P，Argoul P.Continuous wavelet transform for modal identification using free decay response［J］.Journal of Sound and Vibration，2004，277(1-2):73-100.

［2］滕 軍，朱焰煌，周 峰，等.基于復Morlet小波變換的大跨空間結構模態參數識別研究［J］.振動與沖擊，2009，28(8):25-29.

［3］徐曉霞，任偉新，韓建剛.基于響應協方差小波變換和SVD的結構工作模態參數識別［J］.振動工程學報，2010，23(2):194-199.

［4］代 煜，孫和義，李慧鵬，等.基于小波變換的弱非線性阻尼和剛度辨識方法［J］.振動與沖擊，2009，28(2):51-55.

［5］ Boltezar M，Slavic J.Enhancements to the continuous wavelet transform for damping identifications on short signals［J］.Mechanical Systems and Signal Processing，2004，18(5):1065-1076.

［6］伊廷華，李宏男，王國新.基于小波變換的結構模態參數識別［J］.振動工程學報，2006，19(1):51-56.

［7］徐增丙，軒建平，史鐵林，等.LS-SVM在基于小波變換的模態分析中端部效應的應用［J］.中國機械工程，2008，19(13):1614-1620.

［8］Kijewski T，Kareem A.Wavelettransformsforsystem identification in civil engineering［J］.Computer-Aided Civil and Infrastructure Engineering，2003，18(5):339-355.

［9］Yan B F，Miyamoto A，Bruhwiler E.Wavelet transform-based modal parameter identification considering uncertainty［J］.Journal of Sound and Vibration，2006，291(1-2):285-301.

［10］ Delprat N，Escudie B，Guillemain P，et al.Asymptotic wavelet and gaboranalysis:extraction ofinstantaneous frequencies［J］.IEEE Transactions on Information Theory，1992，38(2):644-664.

［11］ Fredric M H，Ivica K.(著)，葉世偉，王海娟(譯).神經計算原理［M］.北京:機械工業出版社，2007.

［12］ Yu K，Ye J，Zou J，et al.Missile flutter experiment and data analysis using wavelet transform ［J］.Journal of Sound and Vibration，2004，269(3-5):899-912.