BBMB方程的Crank-Nicolson差分格式的一種迭代算法

馬維元

(西北民族大學數學與計算機科學學院，甘肅蘭州，730030)

Benjamin-Bona-Mahony-Burgers(BBMB)方程主要是為了描述小振幅的長波在非線性耗散媒介中的傳播而建立的數學模型，在物理中有著重要的意義，對其進行了大量的研究［1－8］，其初邊值問題具體如下:

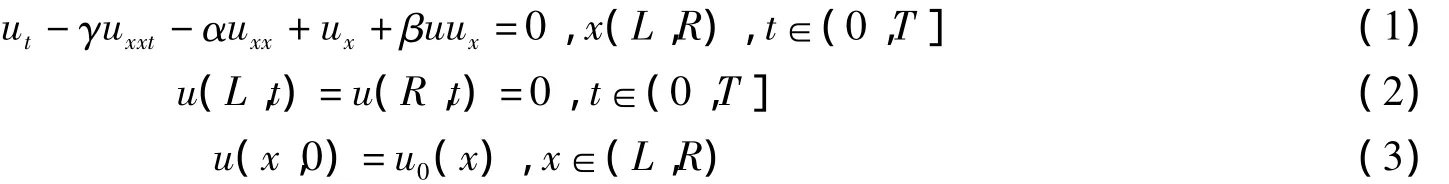
其中 α，β，γ，T＞0。

K.Omrani等［8］提出了BBMB方程的一種Crank-Nicolson差分格式，但是其求解是通過經典的解非線性方程組的Newton迭代法進行的。眾所周知，解非線性方程組的Newton迭代法其求解具有一般性，但是其計算量大，精度也不一定總是很高，因此筆者提出了求解Crank-Nicolson差分格式的一種迭代算法，然后證明了該算法是二階收斂的，最后通過數值例子說明了筆者所提出的算法是有效的。

1 解Crank-Nicolson差分格式的迭代算法

首先回顧一下K.Omrani在文獻［8］提出的Crank-Nicolson差分格式。

通常設J，N為任意正整數，記h=(R－L)/J，τ=T/N分別為空間步長和時間步長。定義空間:

對于v，w∈W，為了方便起見，引入以下記號:

另外，定義φ:W×W→W的雙線性函數，具體為(φ(v，w))i=

定義C為廣義常數與步長h和τ無關，且常數C可在不同的情況下取到不同的值。對于BBMB方程提出的Crank-Nicolson格式如下:

該差分格式的截斷誤差為O(h2+τ2)。對于(4)式，可以改寫為:

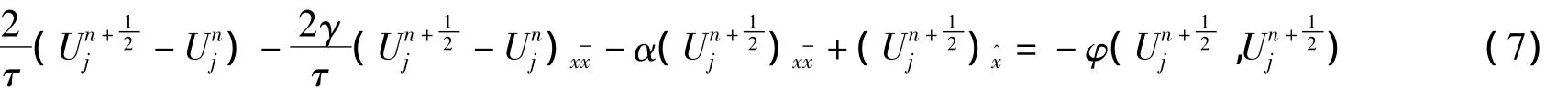
筆者在文獻［9］的基礎上，提出如下的迭代算法:

其中

2 迭代算法的收斂性

下面證明所提出的迭代算法收斂到差分格式。

定理1 假設方程(1)-(3)的解u(x，t)是充分光滑的，當k和τ充分小時，迭代算法(8)以‖·‖∞范數收斂到Crank-Nicolson差分格式(4)-(6)。

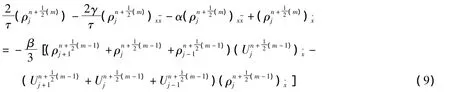
當n=0時，有

當n≥1時，有

從而

當k和τ充分小時，可得

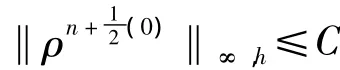
［8］可得

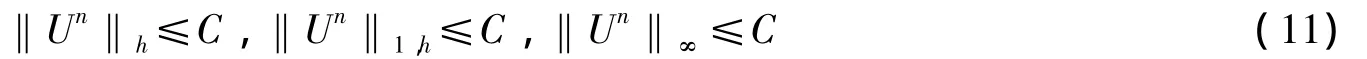
利用(11)式，可得如下的估計式成立

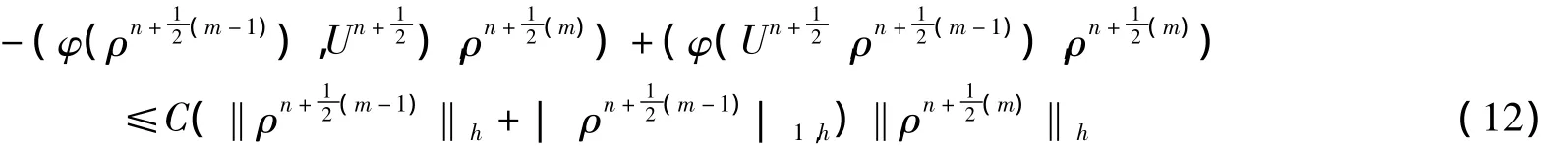
將(12)式帶入(10)式，可得

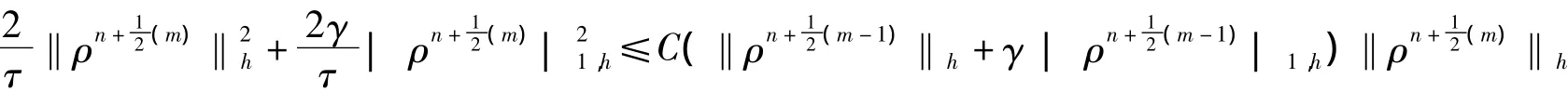
從而

即

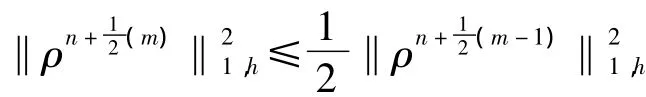
可得

因此，迭代算法(8)以‖·‖1，h范數收斂到Crank-Nicolson差分格式(4)-(6)，再利用離散 Soblev不等式［10］，定理1 得證。

3 數值試驗

在此考慮以下的初邊值問題［1］:

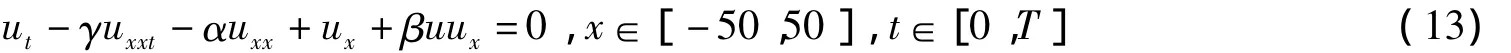
邊界條件為

初始條件為

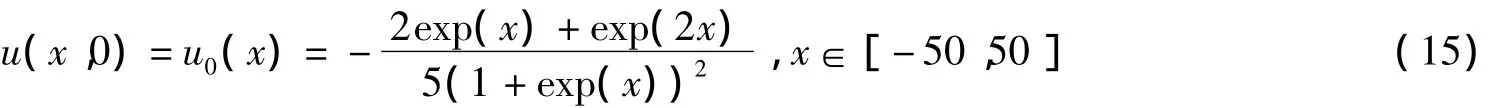
其中α=1，β=12，γ=1。上述問題在(－∞，+∞)上的解為

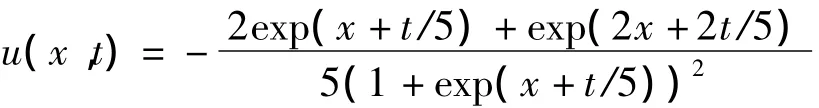
為了數值試驗，將其截斷到區間［－50，50］。

取T=10，分別利用筆者所提出的迭代算法(8)和K.Omrani等在文獻［8］所提到的利用經典的解非線性方程組的牛頓迭代法求解Crank-Nicolson差分格式。當‖∞＜10－10時，讓迭代終止。表1給出了利用牛頓迭代法解BBMB方程的Crank-Nicolson差分格式的誤差的收斂率，表2給出了利用迭代算法(8)解BBMB方程的Crank-Nicolson差分格式的誤差的收斂率。

表1 牛頓迭代法求解BBMB方程的C-N差分格式的誤差的收斂率

表2 迭代算法(8)求解BBMB方程的C-N差分格式的誤差的收斂率

通過對比可以看出，在同樣的時間步長和空間步長下，筆者所提出的算法誤差更小，并且牛頓迭代法并不能驗證K.Omrani等在文獻［8］所證明的二階收斂率，而使用筆者所提出的迭代算法則可以很好的驗證BBMB方程的Crank-Nicolson差分格式的二階收斂率。表3中給出了若每步使用相同的迭代次數，兩種算法的誤差對比，可以看出牛頓迭代法在計算的過程中，損失了很多精度。表4中給出了兩種算法的計算時間對比，可以發現迭代算法(8)在計算時間上遠優于牛頓迭代法。因此，在求解某些非線性方程的Crank-Nicolson差分格式時，使用筆者所提出的迭代算法優于經典的牛頓迭代法。

表3 當h=τ=0.05時，兩種算法的迭代次數與誤差對比

表4 當h=τ=0.05時，兩種算法的CPU時間比較 s

參考文獻:

［1］ WANG M.Exact solution for the Rlw-Burgers equation［J］.Math Appl，1995，8(1):51-55.

［2］ MEIM.Large-time behavior of solution for generalized Benjamin-Bona-Mahony-Burgers Equations［J］.Nonlinear Anal，1998，33(7):699-714.

［3］ ZHANG L.A finite difference scheme for generalized regularized long-wave equation［J］.Appl Math ＆ Comput，2005，168(2):962-972.

［4］ AL-KHALED K，MOMANIS，ALAWNEH A.Approximate wave solutions for generalized Benjamin-Bona-Mahony-Burgers equations［J］.Appl Math Comput，2005，171(1):281-292.

［5］ OMRANIK.The convergence of the fully discrete Galerkin approximations for the Benjamin-Bona-Mahony(BBM)equation［J］.Appl Math Comput，2006，180(2):614-621.

［6］ FAKHARIA，DOMAIRRY G，EBRAHIMPOUR.Approximate explicit solutions of nonlinear BBMB equations by homotopy analysis method and comparison with the exact solution［J］.Phys Lett A，2007，368(1-2):64-68.

［7］ KADRIT，KHIARIN，ABIDIF，et al.Methods for the Numerical Solution of the Benjamin-Bona-Mahony-Burgers Equation［J］.Numer Meth Partial Diff Eq，2008，24(6):1 501-1 516.

［8］ K OMRANI，MAYADI.Finite difference discretization of the Bejamin-Bona-Mahony-Burgers equation［J］.Numer Meth Partial Diff Eq，2008，24(1):239-248.

［9］ KHIARIN，ACHOURIT，MOHAMED M，et al.Finite difference approximate solutions for the Cahn-Hilliard equation［J］.Numer Meth Partial Diff Eq，2007，23(2):437-455.

［10］ ZHOU Y.Application of Discrete Functional Analysis to the Finite Difference Methods［M］.Beijing:International Academic Publishers，1990:1-43.