“繩連接”問題的運動學公式
于希梅 毛安君
(淮陰工學院,江蘇 淮安 223003)
在力學中經常遇到繩連接多個物體的運動問題,繩的連接提供了一個約束條件,各物體的運動量之間將滿足一定的關系式.一般大學物理教材對此類問題往往根據日常經驗直接給出各物體間的速度或加速度關系[1],沒有進行嚴格推導,這種做法在涉及多段繩連接或非慣性系等較復雜問題時容易引起混亂.本文根據運動學的基本公式,應用繩長不變的幾何條件,嚴格推導了各物體滿足的運動學公式,并舉例說明了該公式的應用.
1 運動學公式
如圖1所示,設物體A 和C 用跨過滑輪B 的繩連接,繩不可伸長,對于任意參考系,求A、B、C三者的速度和加速度滿足的關系式.
如圖,對于任意參考點O,A、B、C三者的位矢分別用rA、rB、rC表示,根據幾何關系可知
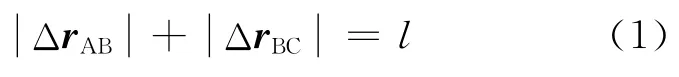
其中,ΔrAB=rB-rA;ΔrBC=rC-rB;l為繩長.因在運動過程中繩長不變,故
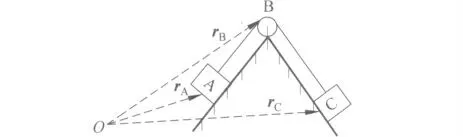
圖1
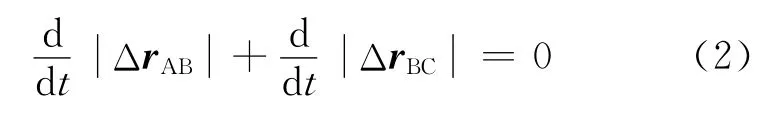
為化簡上式,考慮任意矢量u對時間t的導數

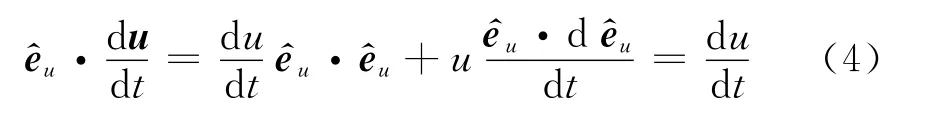
將該結論應用于式(2)

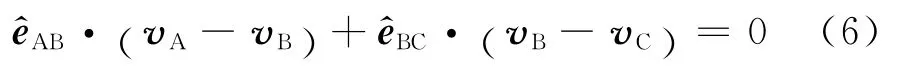
即先將每段繩連接的兩物體的速度之差向該段繩方向上投影,再將各投影求和,則結果為零.該結論很容易推廣到N 個物體由(N-1)段繩連接的情況,相應的關系式為
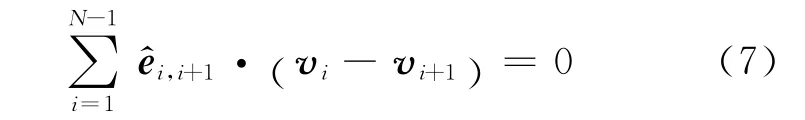
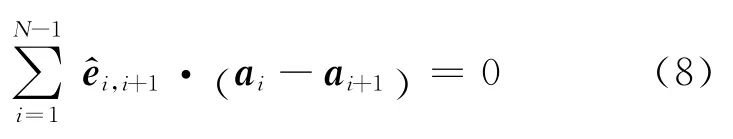
2 應用舉例
例1 如圖2所示,有人用繩繞過定滑輪拉著物體運動,求人和物體運動速率之間的關系.
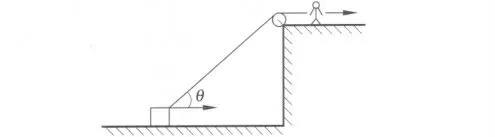
圖2
解答:將物體、滑輪、人三者分別記為A、B、C,應用式(6),注意到vB=0,得vAcosθ-vC=0.
例2 如圖3所示,升降機以加速度a加速上升,A 和C兩物體質量均為m,由跨過定滑輪B的繩連接,A 所在桌面水平,忽略摩擦力和空氣阻力,繩不可伸長,求繩的張力.
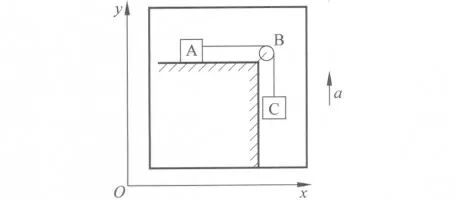
圖3
解答:要求繩的張力,需根據牛頓第二定律列方程,因升降機為非慣性系,故只能選地面參考系,建立坐標系如圖.因運動過程中兩段繩的方向不變,應用式(8)可得
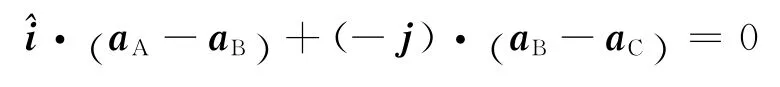
即
(aAx-aBx)-(aBy-aCy)=0
考慮到aBx=0,aBy=a,得aAx+aCy=a.其余過程略.
該題一般解法是先以電梯為參考系,得到A、C兩物體的加速度關系,再根據相對運動的加速度變換式得到以地面為參考系時兩物體的加速度關系,應用公式(8)可直接得到結果,無需對加速度進行參考系間的變換.
例3 如圖4所示,已知A、C 兩物體的質量均為m,物體A 以加速度a向右運動,忽略滑輪和繩的質量,繩不可伸長,求物體A 與桌面間的摩擦力.
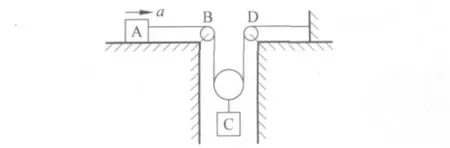
圖4
解答:求A、C 兩物體的加速度關系,應用式(8)
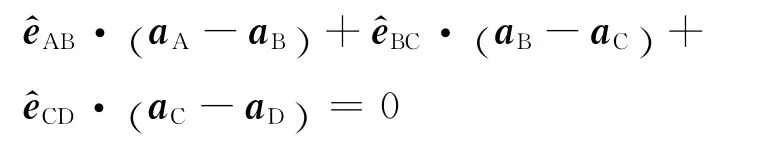
考慮到aB=aD=0,得aA-aC-aC=0,即aC=a/2.余下過程從略.
3 總結
本文給出的公式適用于各種繩連接問題.由于推導過程中沒有應用力學定律,故結果不受慣性系的限制,適用于所有參考系.另外公式以矢量式表達,不受坐標系的限制,可以根據具體問題方便地寫出相應的分量式.如果結合繩受力的形變規律,按照本文思路還可得到變繩長連接的運動學公式.
[1]馬文蔚.物理學[M]5版.北京:高等教育出版社,2006.38~39

