分子間的吸引相互作用在處理實際氣體行為中的影響
張永梅
(中北大學理學院物理系,山西 太原 030051)
實際氣體只有在高溫低壓下近似地符合理想氣體狀態方程,而在高壓低溫下,一切氣體均出現明顯的偏差.如圖1為實驗測得H2在不同溫度下pV-p 曲線[1].可見實際氣體對理想氣體的偏差隨溫度的降低而增大.實際氣體之所以對理想氣體產生偏差,是由于實際氣體不符合理想氣體的微觀模型,即實際氣體的分子間存在相互引力且分子本身有一定的大小.本文在考慮分子大小的前提下,討論了不同形式的分子引力在描述實際氣體行為中的影響.
1 pV-p等溫線
考慮到氣體分子本身的大小,理想氣體狀態方程可修正為p(V-b)=RT,展開可得pV=RT+pb.可見僅考慮分子的體積作用時,pV-p 等溫線是一條直線,與實際氣體的行為偏差很大.下面我們通過在狀態方程中引入不同形式的引力項,分析分子間引力對pV-p 等溫線的影響.
1.1 范德瓦爾斯氣體的pV-p等溫線
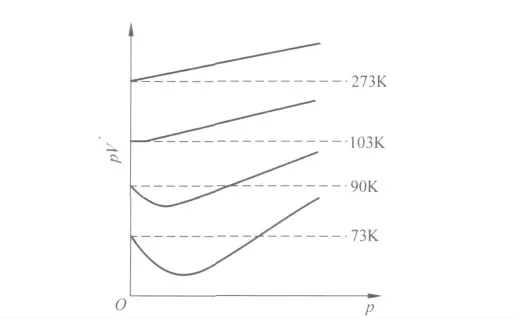
圖1 H2 在不同溫度時的pV-p 關系
1873年荷蘭科學家范德瓦爾斯根據氣體的具體情況,對理想氣體狀態方程作了修正.1 摩爾范德瓦耳斯氣體的狀態方程為
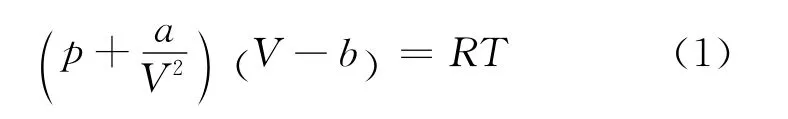
將式(1)展開,可得
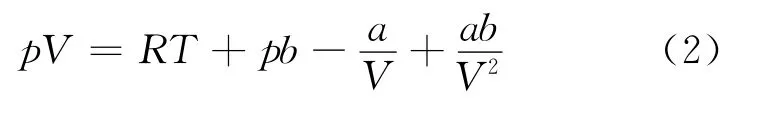
這一方程揭示了實際氣體與理想氣體的微觀差別,它的缺點是方程中吸引項無有關溫度的影響.
1.2 伯塞洛特氣體的pV-p等溫線
考慮到分子間吸引相互作用與溫度有關,伯塞洛特方程在引力項a 中引入了溫度因子.1 摩爾伯塞洛特氣體的狀態方程[2]為
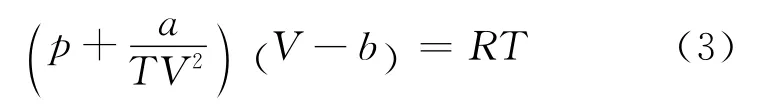
將式(3)展開,可得
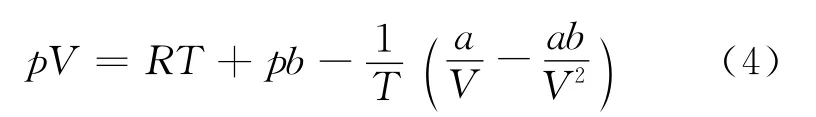
根據式(2)、(4)可得,實際氣體的分子引力和分子體積效應對pV 是兩個相反的影響因素.高溫時,分子間的相互吸引可以忽略,即含a 的項可以略去,從而得到pV=RT+pb,即pV>RT,且隨壓力的升高而增大.在低溫低壓范圍,分子的引力起主要作用,即含b 的項可以略去,可得pV<RT,其數值隨p 的增加而減小.當壓力增大到一定程度,矛盾雙方發生轉化,分子的體積效應變成矛盾的主要方面,于是隨壓力升高pV 值增大.因此在低溫時,是pV 值先隨p 的增加而降低,經過最低點又逐漸上升.比較式(2)、(4)可得,吸引項中溫度因子的引入只是使得吸引項的影響減小.
2 Boyle溫度
pV-p 等溫線中,曲線的最低點移至縱軸上時對應 的 溫 度 定 義 為Boyle溫 度TB[1],可 由 下 式求得
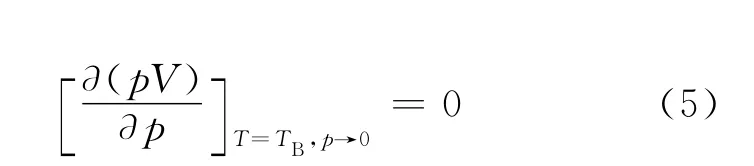
當不考慮引力項時,根據上式可得
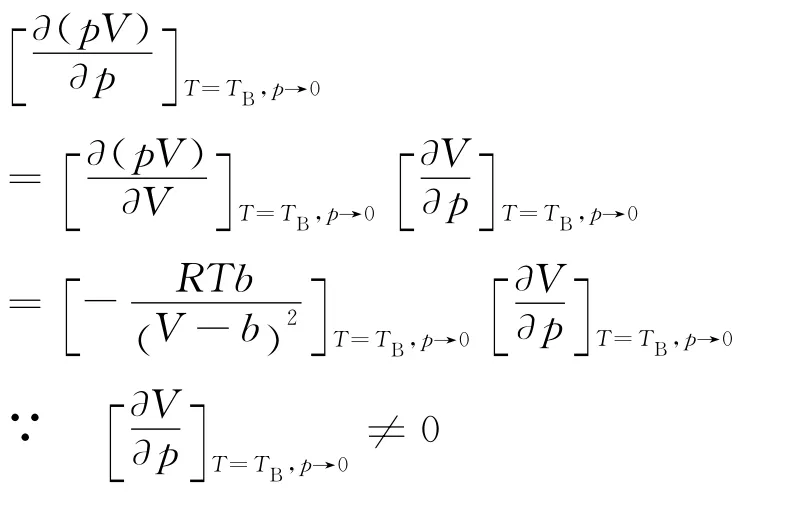
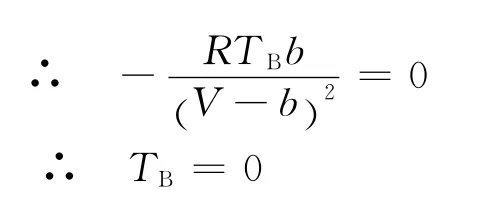
2.1 范德瓦爾斯氣體的Boyle溫度
將式(1)改寫為
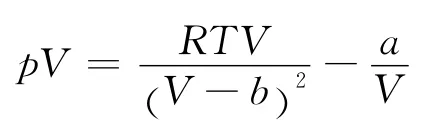
根據式(5)同理可得
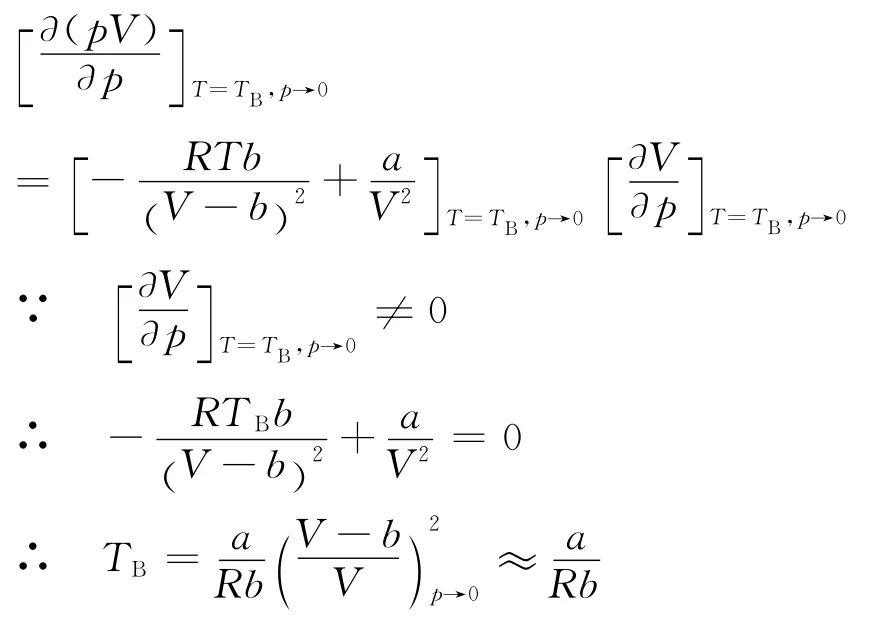
代入a和b 的值可得
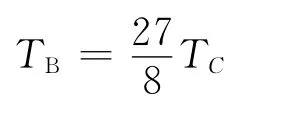
2.2 伯塞洛特氣體的Boyle溫度
將式(3)改寫為
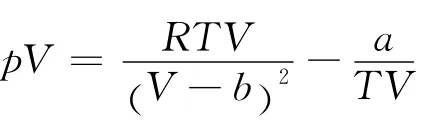
根據式(5)同理可得
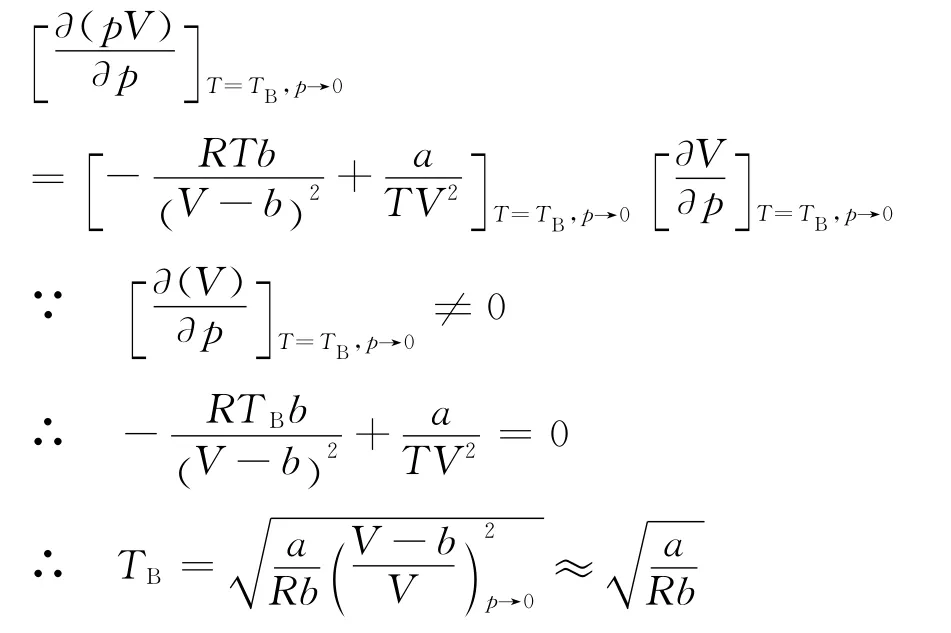
代入a和b 的值可得
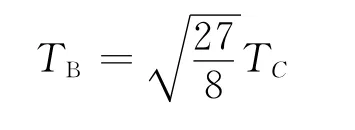
3 結論
通過上面的分析可得出以下結論:
(1)分子間的引力在描述實際氣體行為中具有重要的意義.雖然伯塞洛特氣體狀態方程與范德瓦爾斯氣體狀態方程的展開形式不同,但在對實際氣體的pV-p 等溫線的解釋上,兩種氣體的結論卻完全一致.吸引項中溫度因子的引入只是使得吸引項的影響減小.
(2)當不考慮引力項時,Boyle溫度為零;考慮了引力項后,Boyle溫度與氣體的臨界溫度有關,不同氣體的Boyle溫度不同,這更符合實際氣體的行為.吸引項中的溫度因子只是使Boyle溫度的數值減小,并沒有改變其本質.
[1]朱文濤.物理化學[M].北京:清華大學出版社,1995.9
[2]謝銳生.熱力學原理[M].北京:清華大學出版社,1980.77

