一種基于非均勻馬爾可夫隨機(jī)場的圖像分割方法

張 輝，胡陽漣

（1．咸陽師范學(xué)院 數(shù)學(xué)與信息科學(xué)學(xué)院，陜西 咸陽 712000；2．西安理工大學(xué) 理學(xué)院，陜西 西安 710054）

在圖像處理和計(jì)算機(jī)視覺領(lǐng)域，圖像分割是其中的一個(gè)難點(diǎn)，也是重點(diǎn)。它的目的是將我們感興趣的目標(biāo)從圖像復(fù)雜的背景中提取出來，以便進(jìn)行更深入的分析和處理。圖像分割方法多種多樣，如基于閾值的分割方法，基于邊緣的分割方法，基于內(nèi)容的分割方法，基于統(tǒng)計(jì)的分割方法等。基于馬爾可夫隨機(jī)場（MRF）模型的圖像分割方法[1]，是一種基于統(tǒng)計(jì)的分割方法，以其模型參數(shù)少，空間約束能力強(qiáng)，易于和其他方法相結(jié)合等優(yōu)點(diǎn)，在圖像分割以及其他圖像分析領(lǐng)域中得到了廣泛的應(yīng)用。

基于MRF模型的圖像分割是基于貝葉斯后驗(yàn)概率理論的。一般采用雙MRF，一個(gè)隨機(jī)場對應(yīng)于觀測圖像，另一個(gè)隨機(jī)場對應(yīng)于未知的分類標(biāo)號，通過迭代算法將圖像的局部信息逐步傳遞到整個(gè)圖像，以求得分割標(biāo)號的最大后驗(yàn)概率（MAP）。傳統(tǒng)的基于 MRF模型的圖像分割都是基于均勻MRF隨機(jī)場的，即假定MRF中的耦合系數(shù)是一個(gè)常數(shù)。然而，在許多圖像中，不同的紋理特征有不同的耦合系數(shù)，假定一個(gè)耦合系數(shù)會(huì)帶來分割效果的明顯變差，且不具有自適應(yīng)性。近年來，許多學(xué)者提出了基于非均勻MRF的圖像分割[2]，將圖像建模為一個(gè)非均勻的MRF，改善了分割效果。非均勻MRF與均勻MRF的不同之處在于非均勻MRF采用的是可變的耦合系數(shù)，而均勻MRF的耦合系數(shù)是一個(gè)常數(shù)。一般將圖像分為大小相等的子塊，再用期望最大化（EM）算法[3]估計(jì)每個(gè)子塊中心象素點(diǎn)的耦合系數(shù)，利用線性插值，得到每個(gè)象素點(diǎn)的耦合系數(shù)。由于子塊的劃分沒有利用任何統(tǒng)計(jì)信息和邊緣信息以及相鄰像素之間的相互影響，因此這種估計(jì)方法并不準(zhǔn)確。本文提出在圖像預(yù)分割的基礎(chǔ)上，結(jié)合圖像的統(tǒng)計(jì)性質(zhì)和邊緣信息對圖像進(jìn)行四叉樹分解，把圖像分成不同大小的子塊。再根據(jù)每個(gè)子塊的大小以及子塊內(nèi)邊緣信息的豐富程度，估計(jì)出非均勻MRF的耦合系數(shù)。實(shí)驗(yàn)表明，本文的估計(jì)方法較為準(zhǔn)確，將它應(yīng)用到圖像分割中，能增強(qiáng)圖像分割的自適應(yīng)性，改善分割效果。

1 基于非均勻MRF的圖像分割

圖像分割問題實(shí)際上可以看作是圖像的標(biāo)記問題。平面上的象素點(diǎn)集為 S，滿足 S={s1，s2，ΛΛ，sM×N}，圖像象素點(diǎn)的總數(shù)為M×N。假定得到觀測的圖像數(shù)據(jù)為F，ω為圖像的標(biāo)記場，ω=（ωs1，ωs2ΛΛ，ωsM×N），ωs∈Λ={1，2，ΛΛ，L-1}，L 是類別的總數(shù)。圖像分割問題轉(zhuǎn)化為求解標(biāo)記場ω，使得Bayes后驗(yàn)概率達(dá)到最大。

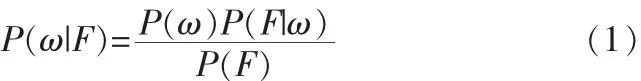
其中P（ω）是標(biāo)記場ω的先驗(yàn)概率，是關(guān)于圖像結(jié)構(gòu)一般性知識的概率描述；P（F|ω）是觀察值F的條件概率分布（也稱為似然函數(shù)）。P（F）是觀測場的概率。因?yàn)橛^測數(shù)據(jù)F是給定的，所以P（F）是一個(gè)常量。因此有：

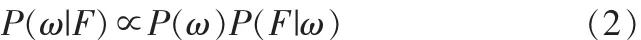
因此只要定義出先驗(yàn)概率P（ω）和似然函數(shù)P（F|ω）就可以把圖像分割問題轉(zhuǎn)化為如下的最優(yōu)化問題：

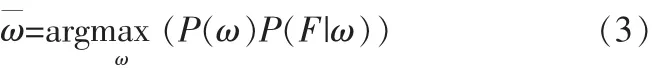
根據(jù)大數(shù)定理，假設(shè)概率P（F|ω）服從高斯分布，且類別λ用它的均值μλ和方差σλ來表示，則似然能量函數(shù)可以表示如下：

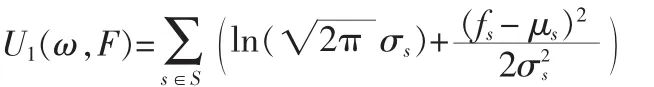
對于先驗(yàn)?zāi)Ｐ停僭O(shè)它符合MRF模型。由Hammersley-Clifford定理[4]可知，一個(gè)馬爾可夫隨機(jī)場與一個(gè) Gibbs隨機(jī)場等價(jià)。因此只要定義了Gibbs隨機(jī)場的能量函數(shù)[5]，那么這個(gè)MRF也就確定了。Gibbs隨機(jī)場的概率密度函數(shù)可以表示為：

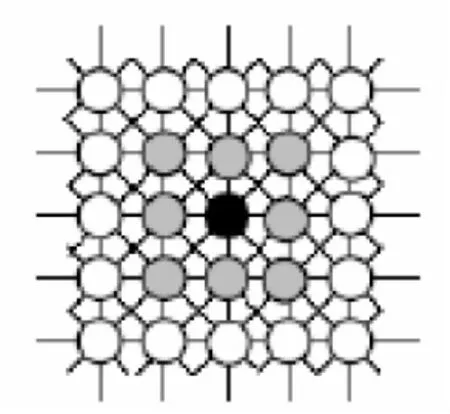
圖1 8-鄰域系統(tǒng)Fig．1 Eight-Neighborhood

因此勢團(tuán)勢能計(jì)算公式可以表示為

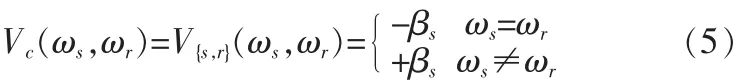
相應(yīng)的先驗(yàn)?zāi)芰亢瘮?shù)為

其中 βs即為像素點(diǎn) S的耦合系數(shù)， 通常在區(qū)間[0．1，2．4]上取值，它控制區(qū)域的同構(gòu)性，在均勻MRF中，βs是一個(gè)常數(shù)。在非均勻MRF中，βs是需要根據(jù)圖像特征去估計(jì)的一個(gè)變數(shù)，這也是均勻MRF和非均勻MRF的不同之處。下面將介紹一種估計(jì)耦合系數(shù)βs的新算法。

2 基于四叉樹分解的耦合系數(shù)估計(jì)方法

2．1 同構(gòu)性的度量

在非均勻MRF中，耦合系數(shù)不是一個(gè)常數(shù)，是隨著圖像中局部的紋理特征而變化的。耦合系數(shù)表征了圖像的同構(gòu)性。在圖像中灰度值分布散亂的區(qū)域，其同構(gòu)性比較弱，耦合系數(shù)也就較小；而在圖像的“塊”較大的區(qū)域，同構(gòu)性比較強(qiáng)，耦合系數(shù)比較大。圖2顯示了耦合系數(shù)和圖像特征之間的關(guān)系。

圖2 耦合系數(shù)與圖像特征的關(guān)系Fig．2 Relation of isomorphic coefficient and image feature

在同一幅圖像中，耦合系數(shù)往往β不是均勻分布的。如圖3中的耦合系數(shù)隨著圖像的散亂程度從左到右逐漸變大。圖4為圖3的耦合系數(shù)的圖像表示。

圖3 散亂程度漸變的圖像Fig．3 Scattered degree gruadually changed image

圖4 耦合系數(shù)的圖像表示Fig．4 Isomorphic coefficient image

通過觀察發(fā)現(xiàn)在同構(gòu)性小的區(qū)域，在進(jìn)行初始分割后，其邊緣信息比較豐富。因此用邊緣信息的豐富程度，來度量圖像在局部的同構(gòu)性。具體做法如下：假如Mi為圖像的一個(gè)子m×m的子塊，di為該子塊內(nèi)邊緣點(diǎn)的個(gè)數(shù)，定義耦合度為：

其中τ1為調(diào)節(jié)因子，它可以調(diào)節(jié)邊緣信息在計(jì)算耦合度時(shí)的權(quán)重。

2．2 基于四叉樹分解的耦合系數(shù)估計(jì)方法

四叉樹分解的基本思想是首先將圖像分為4個(gè)大小相等子塊，在每個(gè)子塊里面計(jì)算其圖像特征（如均方差），如果此特征小于某個(gè)給定的域值，則再將該子塊劃分為4個(gè)相同大小的子塊，如此循環(huán)，直到子塊的大小達(dá)到預(yù)先給定的最小值為止。

這里以耦合度來作為圖像特征，進(jìn)行四叉樹分解，這樣就可以將耦合度比較大的區(qū)域分成比較大的子塊，耦合度比較小的區(qū)域被分解成比較小的子塊。在分解之前先進(jìn)行一次基于均勻MRF的預(yù)分割，迭代少數(shù)幾次即可。采用遞歸的算法，進(jìn)行分解。以下是算法的步驟：

Step1：用基于均勻MRF的圖像分割方法，迭代10～20次，對圖像進(jìn)行預(yù)分割；

Step2：對預(yù)分割后的圖像I進(jìn)行初始劃分，把圖像分為4個(gè)相同大小的子塊I1，I2，I3，I4， 如果Ii的尺寸大于給定的最小尺寸，則轉(zhuǎn)到step3，否則退出程序；

Step3：依次計(jì)算 I1，I2，I3，I4內(nèi)的耦合度，如果子塊 Ii的耦合度 βi小于給定域值 βT，則令 Ii等于 I，轉(zhuǎn)到 step2。

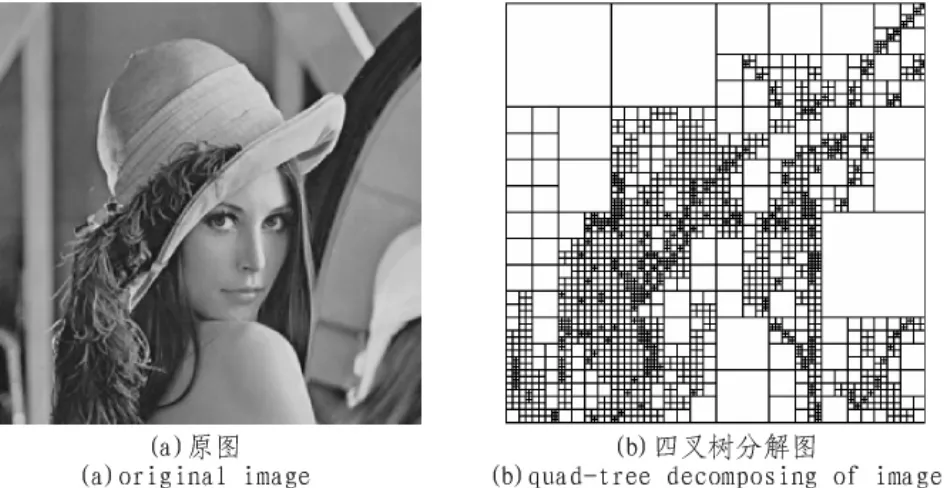
圖5 Lena圖的四叉樹分解Fig．5 Quad-tree decomposing of image Lena

圖5顯示了Lena圖的四叉樹分解。由圖5可以看出，對圖像進(jìn)行四叉樹分解之后，同構(gòu)性小的區(qū)域被分成比較小的子塊，同構(gòu)性比較大的區(qū)域被分成了比較大的區(qū)域。因此可以用子塊的大小來描述耦合系數(shù)的大小。由于耦合系數(shù)的取值一般是在區(qū)間[0．1，2．4]上取值，將區(qū)間進(jìn)行均勻劃分，對應(yīng)不同的子塊尺寸。表1給出了耦合系數(shù)和子塊尺寸之間的對應(yīng)關(guān)系。

表1 子塊尺度與耦合系數(shù)的關(guān)系Tab.1 The relation of the subblocks’sizes and isomorphic coefficient

3 實(shí)驗(yàn)與分析

為了驗(yàn)證本文算法的有效性，我們對兩幅256×256灰度圖像分別用傳統(tǒng)的基于MRF的分割方法和本文提出的方法進(jìn)行了分割。程序的運(yùn)行平臺為賽揚(yáng)2．66 CPU，512 MB內(nèi)存，VC++6．0環(huán)境。本文的馬爾可夫隨機(jī)場求解方法為模擬退火算法，邊緣檢測算子為Sobel算子，預(yù)分割時(shí)的耦合系數(shù)取常數(shù)1．2。基于馬爾可夫隨機(jī)場的圖像分割要用到兩組重要的參數(shù)，及每個(gè)類別λ的均值μλ和方差σλ來。為了精確起見，本文采用樣本訓(xùn)練的方法得到。如圖6所示，選取方框中的特征塊作為樣本，得到每種紋理的均值和方差。分割模型中參數(shù)的取值都取經(jīng)驗(yàn)值，其中初始溫度T=6，溫度調(diào)節(jié)因子α=0．95，加權(quán)系數(shù) τ1=0．08。 從圖 6（c），（d），（e），（f）可以看出，在圖像預(yù)分割以后再進(jìn)行四叉樹分解，可以將圖像的邊緣較豐富的區(qū)域分成比較小的方塊，而邊緣少的區(qū)域被分解成比較大的方塊。而小的方塊對應(yīng)小的耦合系數(shù)，這樣在反復(fù)迭代中就能很好的保護(hù)邊緣。

圖6 待分割圖像及其四叉樹分解Fig．6 Original images and their quad-tree decomposed Images

文中的分割結(jié)果以及傳統(tǒng)的分割結(jié)果如圖7所示。

圖7 分割結(jié)果Fig．7 Result of segmentation

從實(shí)驗(yàn)結(jié)果可以看出，傳統(tǒng)的基于均勻MRF的分割方法中耦合系數(shù)過小容易產(chǎn)生較多孤立點(diǎn)（如圖7（b）以及圖7（e）中圓圈內(nèi)所示），而耦合系數(shù)過大又不能很好的保持邊緣（如圖 7（c）以及圖 7（f）中圓圈內(nèi)所示）。而本文的分割方法采用了自適應(yīng)的耦合系數(shù)估計(jì)方法，從而能夠達(dá)到更為細(xì)膩的分割效果（如圖 7（a）以及圖 7（d）所示），這充分證明了文中方法具有較強(qiáng)的自適應(yīng)性和魯棒性。

4 結(jié) 論

首先簡要闡述了基于非均勻馬爾可夫隨機(jī)場的圖像分割原理及基本方法，然后從對耦合度的研究出發(fā)，提出了一種基于四叉樹分解的耦合系數(shù)估計(jì)方法，并將此估計(jì)方法與基于馬爾可夫隨機(jī)場的圖像分割算法相結(jié)合進(jìn)行了數(shù)值實(shí)驗(yàn)。實(shí)驗(yàn)表明，本文方法與傳統(tǒng)的基于馬爾可夫隨機(jī)場的圖像分割算法相比效果更好，具有更好的自適應(yīng)性。

[1]ZHANGYong-yue，Smith S，Brady M．Hidden Markov random field model and segmentation of brain MR images[M]．FMRIB Technical Report TR00YZ1 Oxford University，2000．

[2]Gu D B，Sun JX．Emimage segmentation algorithm based on an inhomogeneous hidden MRF model[C]//IEE Proc．-Vis．Image Signal Process．，2005．

[3]ZHANG Yong-yue，Brady M，Smith S．Segmentation of brain MR image trough a hidden markov random field modle and the expection-maximination algorithm[J]．IEEE Transactions on Medical Imaging，2006，20（1）：45-57．

[4]Geman S，Geman D．Stochastic relaxation， Gibbs distributions and the Bayesian restoration of images[J]．IEEE Trans．Pattern Anal，1984，26（9）：721-741．

[5]Derin H，Elliott H．Modeling and segmentation of noisy and textured images using Gibbs Random Fields[J]．IEEE Trans，Pattern Anal．Machine Intell，1987，9（1）：39-55．

[6]胡陽漣．基于馬爾可夫隨機(jī)場的圖像分割研究[D]．西安：西安理工大學(xué)，2008．