彈性支撐及連接邊界的多跨曲梁面內自由振動分析

周海軍，李玩幽，呂秉琳，李文龍

(1.哈爾濱工程大學動力與能源工程學院，黑龍江哈爾濱150001;2.韋恩州立大學機械工程學院，底特律48202)

曲梁結構以其結構簡單、強度高等特點在現代土木、航天、船舶、汽車等領域得到越來越多的應用，在其多樣的結構振動中尤其又以面內振動引起了眾多國內外學者的關注.孫建鵬等［1］采用傳遞矩陣法求解了單跨曲線箱型截面梁的固有特性.袁駟等［2］對平面變截面曲梁面內自由振動的自適應有限元法進行了求解分析.武蘭河等［3］通過微分容積法將曲梁自由振動的控制微分方程和邊界方程離散成為一組齊次線性方程組的典型特征值問題，求解得到曲梁自由振動特性.Chidamparam［4］等采用迦遼金法對弓形結構的面內振動進行了研究.眾多學者采用有限元法對各種結構的曲梁進行了研究［5－7］.Kang等［8］采用波傳播方法對面內曲梁系統的自由振動進行了研究.李天勻等［9］、單德山等［10］在振動特性的基礎上進一步研究了曲梁結構的功率流及曲梁結構梁橋的車橋耦合振動.

李文龍［11］提出了一種改進傅里葉級數方法分析任意支撐邊界的直梁振動特性，并將其引入多跨直梁及任意邊界板結構分析［12－14］.

本文基于李提出的方法，對多跨曲梁面內自由振動特性進行求解分析.將曲梁面內徑向和切向位移函數表示成傅里葉級數加上一個輔助多項式函數的形式.采用瑞利－里茨方法求解基于能量原理的哈密頓方程，得到關于未知位移幅值系數的標準特征值問題.將支撐及連接邊界定義為各個方向的彈性剛度，可以通過設定數值大小簡單地實現對各種傳統邊界的模擬，同時可以研究在彈性支撐與連接下的固有特性.

1 多跨曲梁理論

如圖1所示的多跨曲梁結構，其支撐及連接都由彈性剛度提供.ki，w0和 ki，w1，Ki，w1和 Ki，w0，ki，μ0和ki，u1分別為第i段曲梁在左右兩端的徑向，扭轉，切向支撐剛度分別為第i和i+1段曲梁之間3個方向的連接剛度.

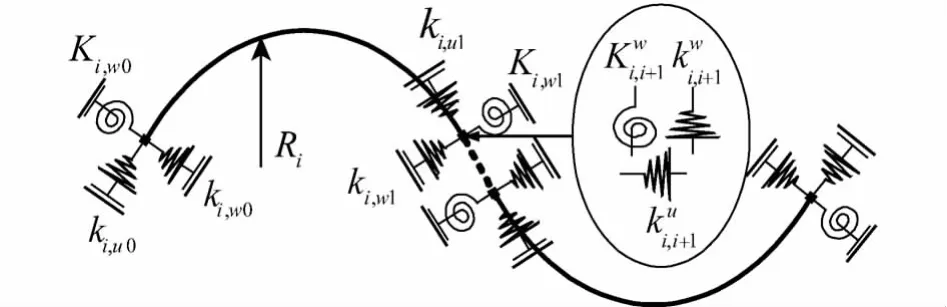
圖1 多跨曲梁模型Fig.1 Model of multi-curved beams

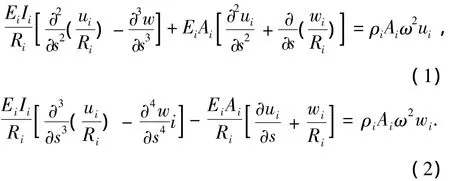
其面內振動控制微分方程為

式中:ui、wi、Ei、Ii、Ri、ρi和Ai分別為切向位移、徑向位移、楊氏模量、慣量、半徑、密度和截面積，s為曲線坐標，ω為圓頻率.

其應變εi，轉角φi，曲率變化χi可以表示為

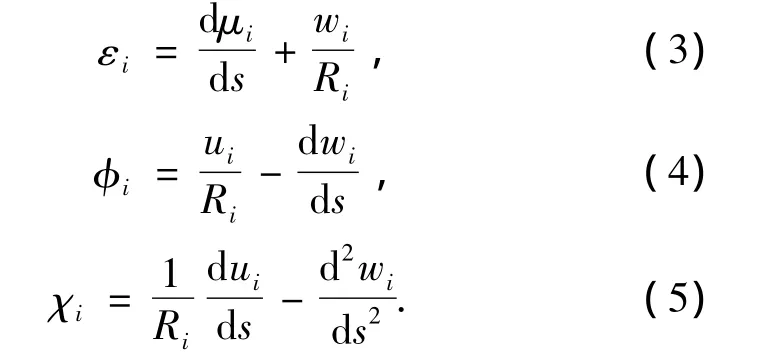
將切向和徑向位移寫成如下形式:

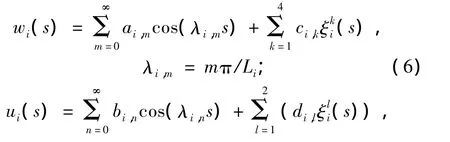
其中，

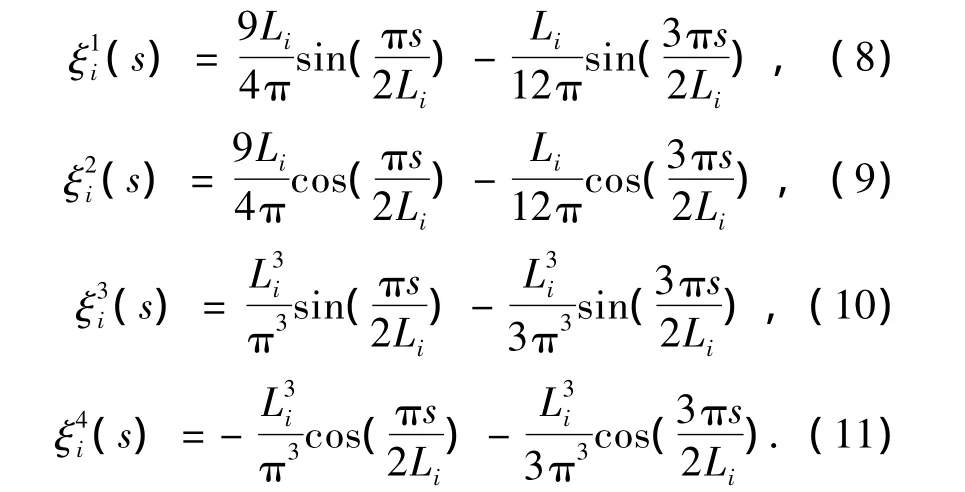
基于能量原理的哈密頓方程表示為

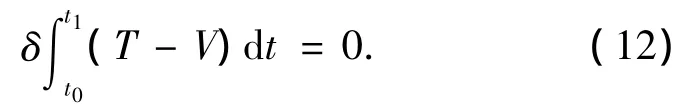
其中將總的勢能V定義為

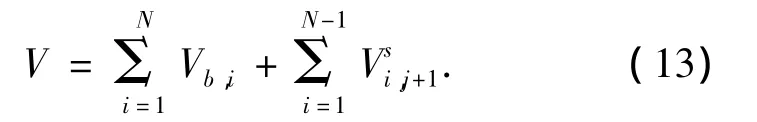
式中:N表示曲梁跨數.

將總的動能表示為

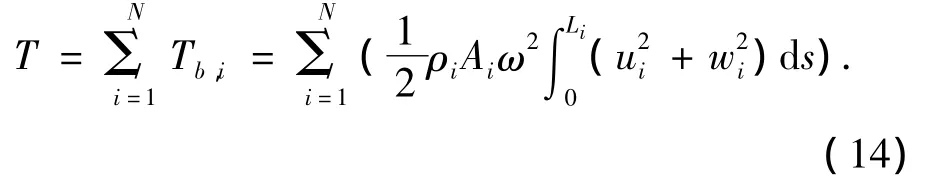
在式(13)中Vb，i表示曲梁i的勢能:

式中:右邊第1、3項括號內為負號時表示曲梁i和i+1有相同的曲率法線方向時的表達式;而正號為相反時的表達式.

根據瑞利－里茨方法求解，先將位移表達式(6)、(7)代入式(13)、(14)，之后對每個未知幅值系數求導并令其等于0.例如，當有相同曲率時對未知系數ai，m'求導得到的方程為

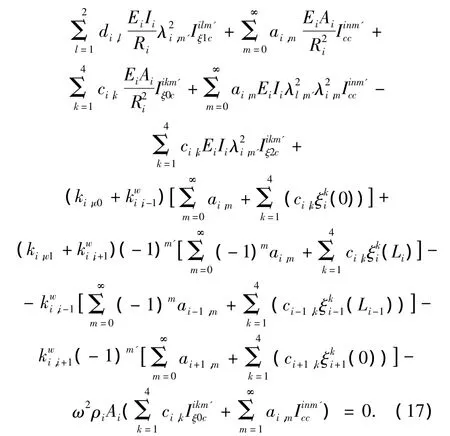
其中:

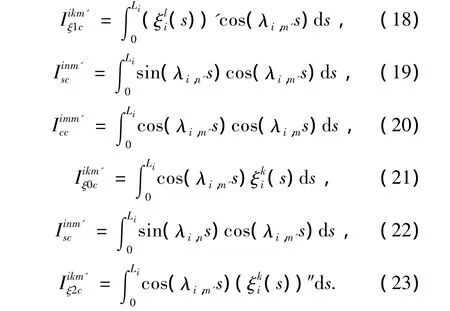
其他未知系數的求導表達式不再一一給出.

將式(6)、(7)中的傅里葉級數展開截斷到m= M和n=N之后，將求導得到的方程整理成矩陣表達形式:

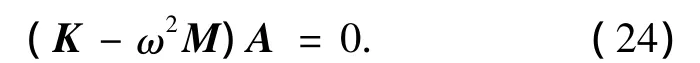
2 單跨及雙跨曲梁結果分析

首先考慮一個在不同傳統邊界，即在固支，簡支及自由邊界條件下單跨曲梁的振動特性，其參數為: E=2.1×1011Pa，I=7.854 0×10－9m4，R=1 m，ρ=7 800 kg·m－3，A=3.141 59×10－4m2，以及L =1.047 2 m(即一個半徑為1 m，跨度為60°的曲梁長度).文中傅里葉級數展開到M=N=20.將彈簧剛度系數設置為0或一個無窮大數可以模擬自由或固支邊界，本文數值取k=1×1012N·m－1.表1～3列出了其前10階固有頻率與在有限元軟件ANSYS中仿真結果的對比.有限元模型中曲梁劃分成30個單元.

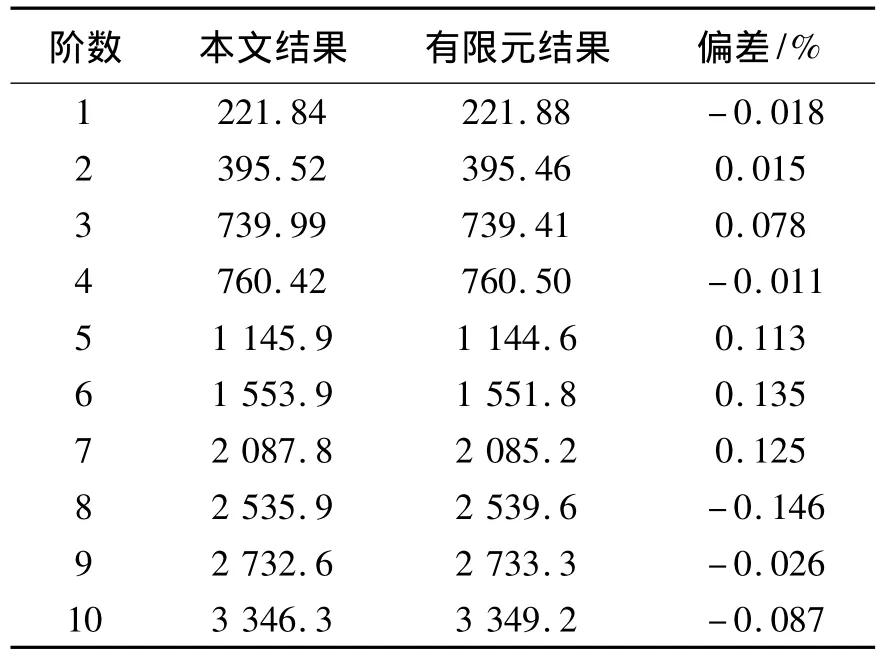
表1 單跨曲梁固支邊界結果對比Table 1 The comparing results of a single-span curved beam with C-C boundary conditions

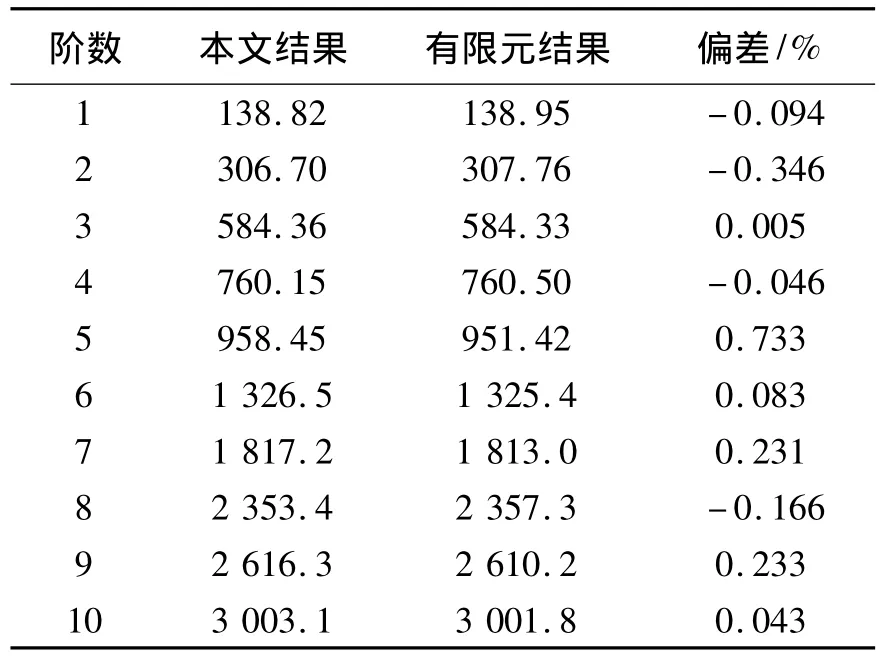
表2 單跨曲梁簡支邊界結果對比Table 2 The comparing results of a single-span curved beam with S-S boundary conditions

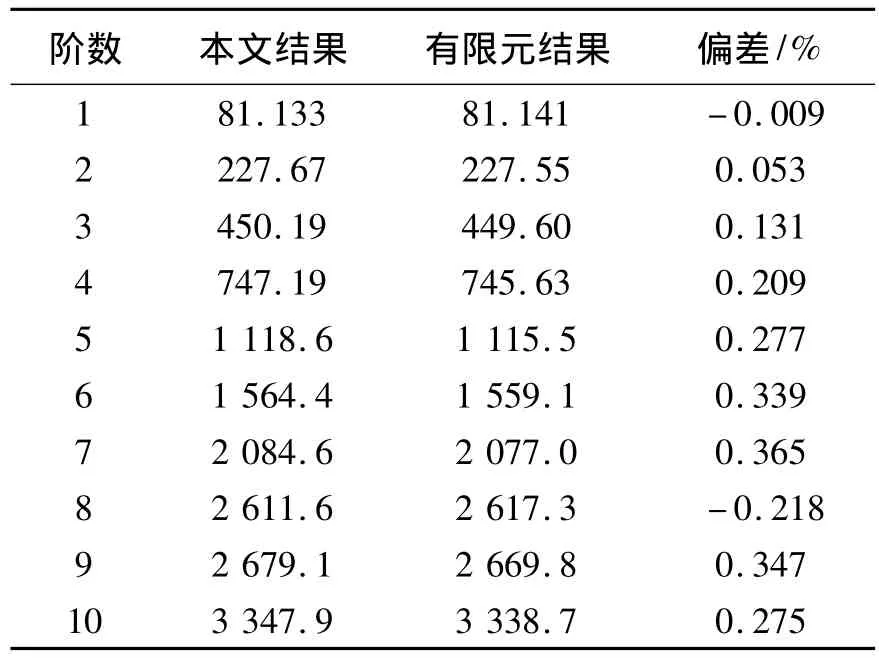
表3 單跨曲梁自由邊界結果對比Table 3 The comparing results of a single-span curved beam with F-F boundary conditions

圖2為固支邊界前四階振型與ANSYS所得振型的對比.將其振型分解到整體坐標x，y方向，歸一化到1之后進行對比.由固有頻率和振型的對比可以看出本文方法是正確的.

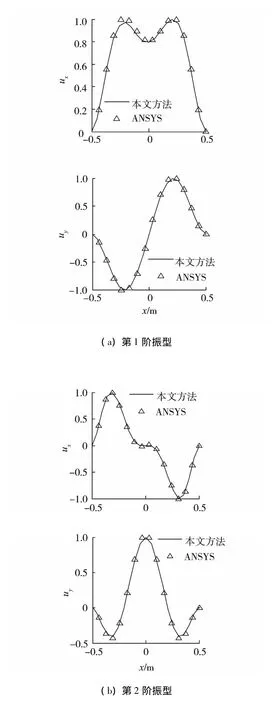
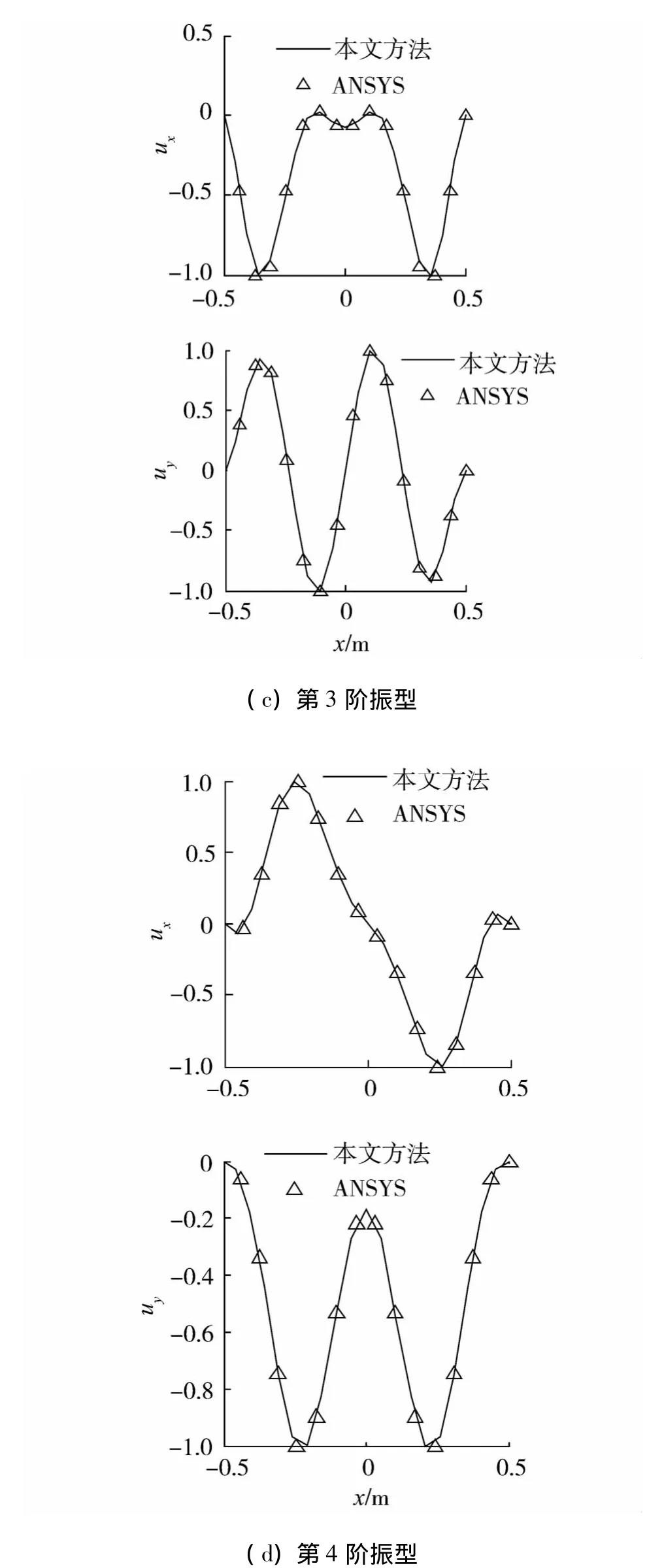
圖2 前四階振型與有限元的對比Fig.2 The first four mode shapes compared with FEA results

選取一個L=1.570 8 m(即一個半徑為1 m，跨度為90°的曲梁長度)，其他參數同上一個算例，將徑向和切向支撐剛度設定為k=5×105N·m－1，扭轉支撐剛度設定為k=0 N·m－1以模擬彈性支撐邊界.其前10階固有頻率與在有限元軟件ANSYS中仿真結果的對比見表4，可見彈性邊界結果也是正確的.

表4 單跨曲梁彈性邊界結果對比Table 4 The comparing results of a single-span curved beam with elastic boundary conditions

為了驗證本文在多跨曲梁處理的正確性，選擇了一個兩跨曲梁模型，每跨曲梁的參數都與第1個算例相同，兩跨曲梁擁有相反的曲率方向.兩端邊界取為固支邊界，連接剛度也取為剛性，其剛度參數設置具體為:k1，w0=K1，w0=k1，u0=1×1012N·m－1，k2，w1=K2，w1=k2，u1=1×1012N·m－1，k1，w1=K1，w1=k1，u1=0 N·m－1，k2，w0=K2，w0=k2，u0=0 N·m－1以及.表5列出了其前10階固有頻率與有限元軟件ANSYS中仿真結果的對比.

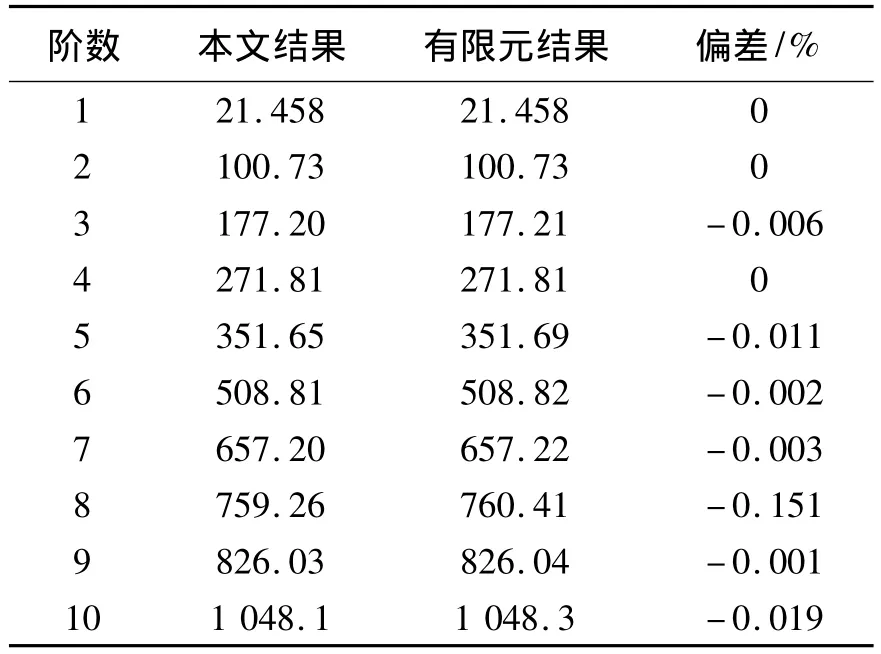
表5 雙跨曲梁固支邊界結果對比Table 5 The comparing results of a two-span curved beams with C-C boundary conditions

圖3列出了前四階振型.圖3(a)中為第1和第3階振型，為對稱振型;圖3(b)中為第2和第4階振型，為反對稱振型.可以看出在多跨曲梁的處理上也是正確的.

圖3 前四階振型Fig.3 The first four mode shapes

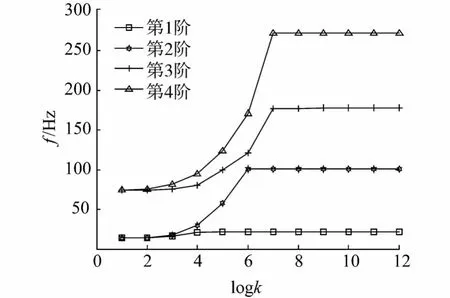
圖4 兩跨曲梁中間連接剛度對其前4階頻率的影響Fig.4 The effect of connecting stiffnesses between twospan curved beams on the first four frequencies

3 結論

本文采用一種改進的傅里葉級數方法，對多跨曲梁面內自由振動特性進行求解分析.采用瑞利－里茨方法求解基于能量原理的哈密頓方程，得到關于未知位移幅值系數的標準特征值問題.將支撐及連接邊界定義為各個方向的彈性剛度，可以通過設定數值大小簡單地實現對各種傳統邊界的模擬，同時改變連接彈簧勢能中的正負號可以模擬具有相同或相反曲率法線方向的多跨曲梁.求解了單跨固支、簡支、自由邊界及彈性支撐邊界模型結果及兩跨固支、相反曲率法線方向模型的結果，通過與有限元軟件ANSYS模型所得結果的對比驗證了方法的正確性.并分析了兩跨固支曲梁中間連接剛度對固有頻率的影響，中間連接剛度的降低首先影響到高階頻率，并且都在某個剛度區域發生頻率的突然變化.

［1］孫建鵬，李青寧.基于傳遞矩陣法曲線橋的振動特性分析［J］.西安建筑科技大學學報:自然科學版，2009，41 (4):518－523.

SUN Jianpeng，LI Qingning.The vibration characteristic analysis of curved bridge based on transfer matrix method［J］.Journal Xi＇an University of Architecture＆Technology:Natural Science Edition，2009，41(4):518－523.

［2］袁駟，葉康生，王珂.平面曲梁面內自由振動分析的自適應有限元法［J］.工程力學，2009，26(增刊):126－132.

YUAN Si，YE Kangsheng，WANG Ke.A self－adaptive FEM for free vibration analysis of planar curved beams with variable cross－sections［J］.Engineering Mechanics，2009，26(Suppl.):126－132.

［3］武蘭河，劉淑紅，周敏娟.圓弧曲梁面內自由振動的微分容積解法［J］.振動與沖擊，2004，3(1):117－122.

WU Lanhe，LIU Shuhong，ZHOU Minjuan.Differential cubature method for in－plane vibration analysis of shear deformable curved beams［J］.Journal of Vibration and Shock，2004，3(1):117－122.

［4］CHIDAMPARAM P，LEISSA A W.Influence of centerline extensibility on the in－plane free vibrations of loaded circular arches［J］.Journal of Sound and Vibration，1995，183: 779－795.

［5］YANG S Y，SIN H C.Curvature－based beam elements for the analysis of Timoshenko and shear－deformable curved beams［J］.Journal of Sound and Vibration，1995，187: 569－584.

［6］RAVEENDRANATH P，SINGH G，PRADHAN B.Free vibration of arches using a curved beam element based on a coupled polynomial displacement field［J］.Computers and Structures，2000，78:583－590.

［7］YANG F，SEDAGHATI R，ESMAILZADEH E.Free inplane vibration of general curved beams using finite element method［J］.Journal of Sound and Vibration，2008，318: 850－867.

［8］KANG B，RIEDEL C H，TAN C A.Free vibration analysis of planar curved beams by wave propagation［J］.Journal of Sound and Vibration，2003，260:19－44.

［9］李天勻，張小銘.周期簡支曲梁的振動波和功率流［J］.華中理工大學學報，1995，23(9):112－115.

LI Tianun，ZHANG Xiaoming.The vibration wave and power flow in a periodical simply supported curved beam［J］.Journal of Huazhong University of Science＆Technology，1995，23(9):112－115.

［10］單德山，李喬.鐵路曲線連續梁車橋耦合振動研究［J］.振動與沖擊，2005，24(4):62－67.

SHAN Deshan，LI Qiao.Vibration analysis of railway continuous curved－girder bridge coupled with vehicles［J］.Journal of Vibration and Shock，2005，24(4):62－67.

［11］LI W L.Free vibration of beams with general boundary conditions［J］.Journal of Sound and Vibration，2000，237:709－725.

［12］DU J T，LI W L，JIN G Y，et al.An analytical method for the in－plane vibration analysis of rectangular plates with elastically restrained edges［J］.Journal of Sound and Vibration，2007，306:908－927.

［13］XU Hongan，LI W L.Vibrations of multi－span bridges under a moving load:effect of the coupling conditions between spans［J］.Journal of Sound and Vibration，2008，312:736－753.

［14］ZHANG X，LI W L.Vibrations of rectangular plates with arbitrary non－uniform elastic edge restraints［J］.Journal of Sound and Vibration，2009，326:221－234.