Spectrum-generating超代數(shù)的一類子代數(shù)的研究

郭娜，劉東，高壽蘭

（1.杭州電子科技大學(xué)理學(xué)院，浙江杭州 310000；2.湖州師范學(xué)院理學(xué)院，浙江湖州 313000）

Spectrum-generating超代數(shù)的一類子代數(shù)的研究

郭娜1，劉東2，高壽蘭2

（1.杭州電子科技大學(xué)理學(xué)院，浙江杭州 310000；2.湖州師范學(xué)院理學(xué)院，浙江湖州 313000）

研究spectrum-generating超代數(shù)的一類子代數(shù)，確定了這類子代數(shù)的低階上同調(diào)群以及自同構(gòu)群.這類子代數(shù)對于討論N=2-超共形代數(shù)上Harish-Chandea模的分類很有意義.

李超代數(shù)；導(dǎo)子代數(shù)；中心擴張；自同構(gòu)

1 引言

超共形代數(shù)與共形場論和弦理論緊密聯(lián)系，在數(shù)學(xué)與物理學(xué)有重要作用.N=2-超共形代數(shù)[1]是復(fù)維數(shù)-D的Calabi-Yau流形上的弦緊致分析的基本工具[2].它的表示理論和Kac-Roan-Wakimoto猜想有關(guān)[3].為了對N=2-超共形代數(shù)上的Harish-Chandra模進行分類，我們需要研究下面的李超代數(shù)，它是Spectrum-generating超代數(shù)的一個子代數(shù)[4].

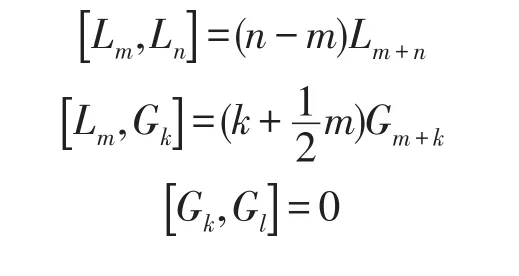
本文重點討論李超代數(shù)A的結(jié)構(gòu)理論，包括它的導(dǎo)子代數(shù)、二上同調(diào)群、自同構(gòu)群等.我們分別用C，Q 和Z來定義復(fù)數(shù)集、有理數(shù)集和整數(shù)集.對于任意集合S，定義它的非零元素集合為S*.

2 泛中心擴張

首先我們回顧李超代數(shù)L上的二上循環(huán)，它是C-雙線性函數(shù)：ψ：L×L→C并且滿足下面的關(guān)系式：

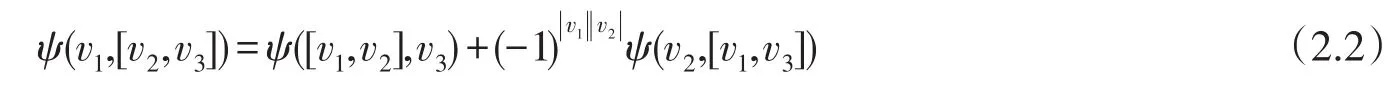
對任意的v1,v2,v3∈L，定義L上的二上循環(huán)的向量空間為C2(L,C).

對任意的C-線性函數(shù)f：L→C，定義二上循環(huán)ψf如下：對任意的v1,v2∈L，ψf(v1,v2)=f([v1,v2]).

這樣的二上循環(huán)我們稱為L上的二上邊界或者平凡二上循環(huán).

定義L的二上邊界的向量空間為B2(L,C).如果φ-ψ是平凡的，那么我們稱二上循環(huán)φ與二上循環(huán)ψ是等價的.對于一個二上循環(huán)ψ，定義它的等價類為[ψ].商空間H2(L,C)=C2(L,C)/B2(L,C)=｛二上循環(huán)的等價類｝，被稱為L的二階上同調(diào)群.

眾所周知，Virasoro循環(huán)的二上循環(huán)由下式確定：

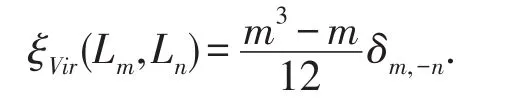
定理1dimH2(A,C)=2，其中關(guān)于A的常見的不平凡二上循環(huán)如下：

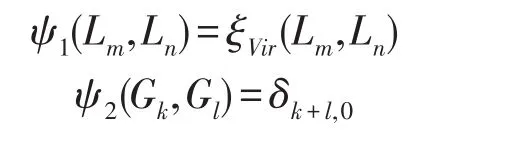
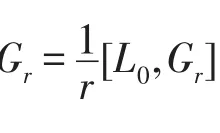
令φ=ψ-ψf-ξVir，其中ψf滿足ψf(v1,v2)=f([v1,v2]).那么我們得到φ(Lm,Ln)=0對任意的m,n∈Z成立.

定理1可由下面的引理1-3得到.

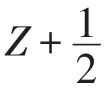
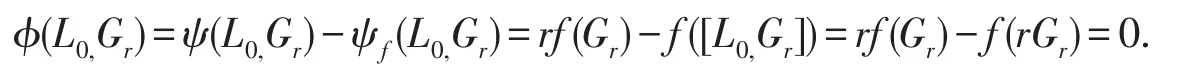
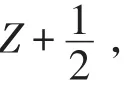
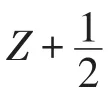
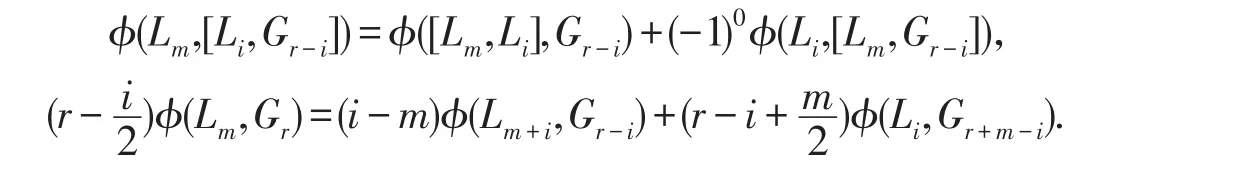
令i=0，即

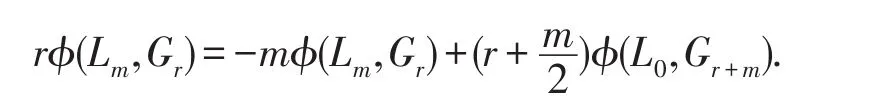
由于φ(L0,Gr+m)=0，那么(r+m)φ(Lm,Gr)=0.

因為r+m≠0，所以φ(Lm,Gr)=0.

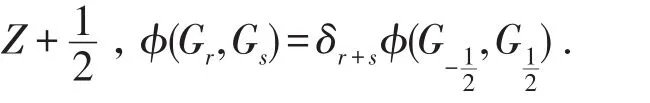
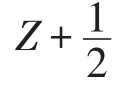
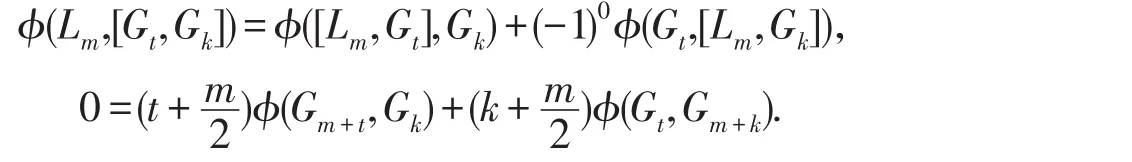
令m=-2t，就得到如果t+k≠0，φ(Gt,Gk)=0.

令t=-(k+m)，

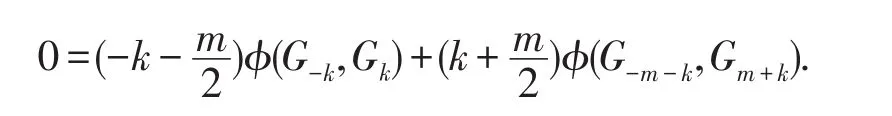
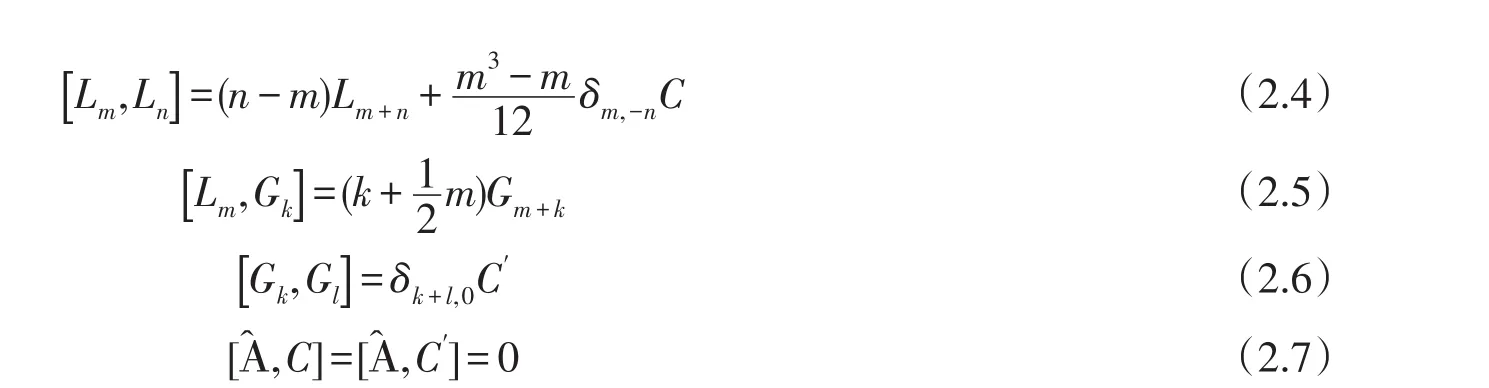
3 算子Lm,Gk的構(gòu)造

本節(jié)中，當(dāng)C=C′=1時，我們利用一些算子去構(gòu)建上述李超代數(shù)A^.

我們利用Fermionic振子ψn，并且它滿足反交換關(guān)系

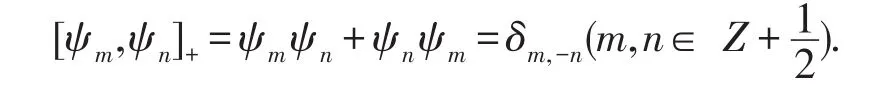
上述代數(shù)可以由下面的向量空間表示：

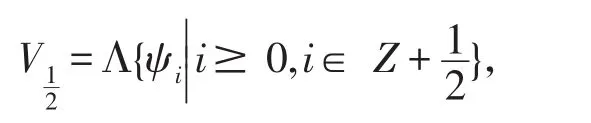
其中符號Λ表示由ψi生成的外代數(shù).

令Lk(k∈Z)是Vδ中的算子，定義：

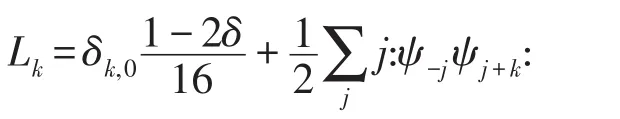
其中j跑遍δ+Z并且正常序列定義為

那么：

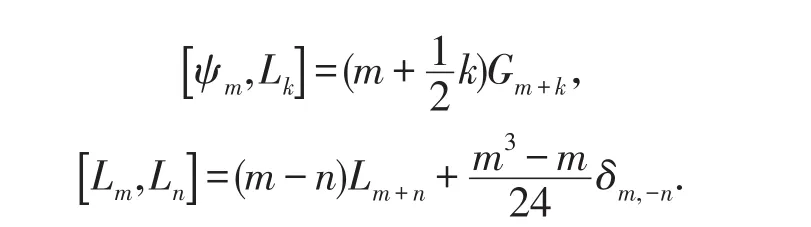
所以為了構(gòu)建這個代數(shù)，我們僅需要將ψk替換為Gk，那么關(guān)系式（2.4）-（2.7）成立.

4 李超代數(shù)A的導(dǎo)子

令V是一個A-模.從A到V的線性映射φ叫做導(dǎo)子，如果對任意的x,y∈A，我們有

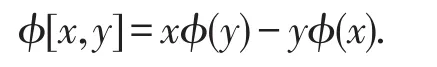
當(dāng)v∈V，映射φ:x→x·v叫做內(nèi)導(dǎo)子.所有導(dǎo)子的向量空間定義為Der(A,V).所有內(nèi)導(dǎo)子的向量空間定義為Inn(A,V).那么在V中的A的一階上同調(diào)群和它們的系數(shù)關(guān)系為等式右邊同時也叫做外導(dǎo)子空間.

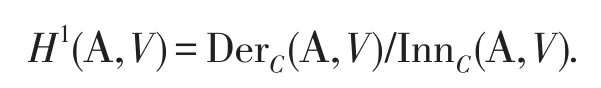
首先我們介紹A的外導(dǎo)子δ：

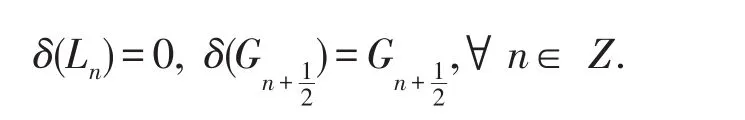
引理4Der(A,V)=Der(A,V)0+Inn(A,V)，其中Der(A,V)0={D∈Der(A,V)|D(Ln)?Vn,對任意的n∈Z}.

證明從文獻[5]很容易得到（證明略）.

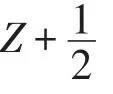
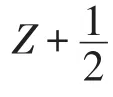
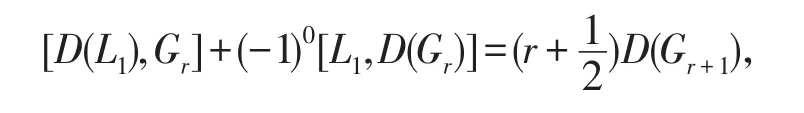
那么

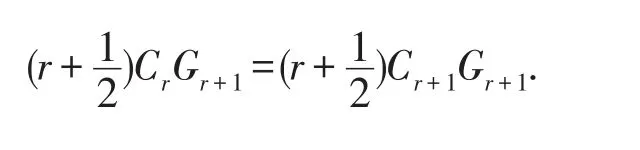
比較Gr+1的系數(shù)，我們有

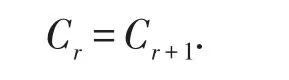
從引理4和引理5，我們可以得到下面的結(jié)論.

定理2

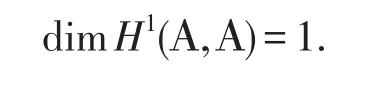
5 自同構(gòu)群

定義AutA為自同構(gòu)群.我們知道，對任意的σ∈AutA，σ(Liˉ)=Liˉ，iˉ∈Z2.

定理3令σ∈AutA，則存在a,b∈C*和ε∈{±1}滿足

反之，如果σ是A上的一個線性函數(shù)滿足（5.1）-（5.3），ε∈{±1}和a,b∈C*，那么σ∈AutA.

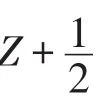
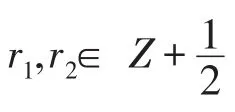
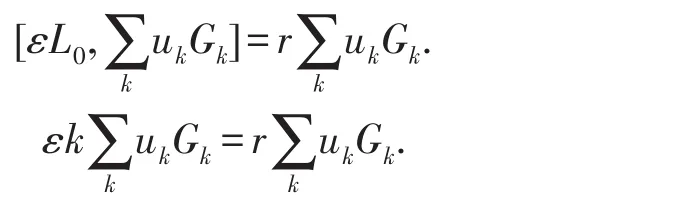
比較Gk的系數(shù)，得到εk=r.因此，

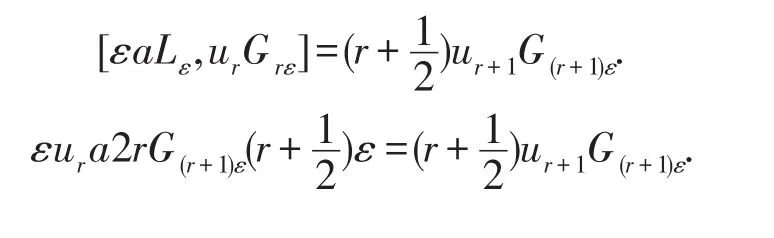
比較G(r+1)ε的系數(shù)，則aur=ur+1.

所以假設(shè)

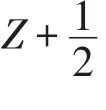
定義A的自同構(gòu)為σ(ε,a,b)滿足（5.1）-（5.3），那么

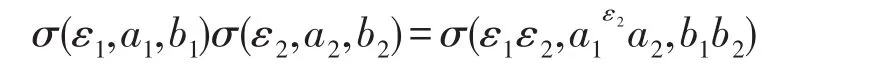
和

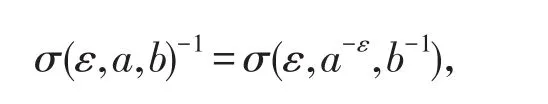
當(dāng)且僅當(dāng)ε1=ε2,a1=a2,b1=b2.

通過上面的討論，我們很容易得到下面的定理：

定理4AutA=Z2∝(C*×C*)

[1]Dobrev V K.Characters of the unitarizable highest weight modules over the N=2 superconformal algebras[J].Phys Lett,1987,B (186):43-51.

[2]Eguchi T,Hikami K.N=2 superconformal algebra and the entropy of Calabi-Yau manifolds[J].Lett Math Phys,2010,92(3):269-297.

[3]Arakawa T.Representation theory of superconformal algebras and the Kac-Roan-Wakimoto conjecture[J].Duke Math J,2005,130 (3):435-478.

[4]Ademollo M,Brink L,Adda A D,et al.Supersymmetric strings and colour confinement[J].Phys Lett,1976,B(62):105-110.

[5]Farnsteiner R.Derivations and central extensions of finitely generated graded Lie algebra[J].J Algebra,1998,118:33-45.

[6]Fuks D B.Cohomology of Infinite-Dimensional Lie Algebras[M].New York:Springer,1986:119-120.

A Study of One Subalgebra of the Spectrum-generating Superalgebra

GUO Na1,LIU Dong2,GAO Shou-lan2
(1.Depaprtment of Sciences and Mathematics,Hangzhou Dianzi University,Hangzhou 310000,China;2.Department of Sciences and Mathematics,Huzhou Teachers College,Huzhou 313000,China)

One subalgebra of spectrum-generating superalgebra is studied in this paper.And low order cohomology group and the automorphism group of this algebra are also determined in the paper.This subalgebra is helpful to classified Harish-Chandea modules over the N=2 superconformal algebra.

Lie superalgebra;derivation algebra;central extensions;automorphism

O152.5

A

1008-2794（2012）10-0027-05

2012-08-21

國家自然科學(xué)基金項目“Virasoro代數(shù)及相關(guān)代數(shù)的結(jié)構(gòu)與表示理論”（11071068）；國家自然科學(xué)基金項目“共型流李代數(shù)的結(jié)構(gòu)和表示”（11201141）；浙江省自然科學(xué)基金項目“Virasoro型李代數(shù)與頂點算子代數(shù)的研究”（Y6100148）；浙江省自然科學(xué)基金項目“無限維李代數(shù)與頂點算子（超）代數(shù)的結(jié)構(gòu)域表示”（LQ12A01005）

郭娜（1986—），女，河南南陽人，杭州電子科技大學(xué)2010級研究生，研究方向：李代數(shù).