車用往復式真空泵的設計方法

上官文斌 楊嘉威 林浩挺 劉宏慈 蔣開洪

（1.華南理工大學；2.寧波拓普集團股份有限公司）

1 前言

車用真空泵的主要類型有葉片式、膜片式以及往復式。我國車用真空泵以葉片式真空泵為主，但其可靠性及耐久性較差、價格昂貴，因而使用受到限制。相對于葉片式和膜片式真空泵，往復式真空泵綜合性能良好且振動噪聲性能優越。

目前關于真空泵的研究大都局限于抽水泵、羅茨真空泵、渦輪、分子泵[1～4]。這些真空泵額定轉速低、體積大、單位體積抽速小，其研究成果不能直接用于轉速高、體積小的車用真空泵。本文介紹了往復式真空泵的結構和工作原理，給出了車用真空泵的評價標準，建立了一套往復式真空泵制動性能的計算分析方法。實測了某款往復式真空泵的性能，對比分析了真空泵性能的計算結果和測試結果。

2 往復式真空泵結構及其工作原理

往復式真空泵的結構如圖1所示，其是由兩組平行對置安裝的活塞－氣缸－進排氣單向閥組件構成的具有進排氣功能的部件。其中，排氣單向閥安裝在活塞頂端，進氣單向閥與排氣單向閥之間的空腔構成了氣缸；兩邊的活塞由一個曲柄雙連桿機構帶動，其動力來源于電機；排氣口與大氣相連通，抽氣口與真空助力器伺服氣室相連通。此外，還有氣體消聲器、機座、密封套等輔助部件。

往復式真空泵的工作過程可分為抽氣過程和排氣過程。如圖1所示，電機帶動曲柄雙連桿機構運轉，左、右活塞做往復運動。當活塞由左向右運動時，左邊氣缸的體積將不斷增大，氣缸內氣壓不斷減小；當左邊氣缸內氣壓小于抽氣口處氣壓時，進氣單向閥打開，完成左邊氣缸的抽氣過程。與此同時，右邊氣缸內的體積不斷減小，氣缸內的氣體被壓縮，氣壓不斷增加。當右邊氣缸的氣壓大于排氣口處氣壓時，排氣單向閥打開，完成右邊氣缸的排氣過程。

由此可見，在偏心驅動軸運動一圈的過程中，左、右兩邊的活塞－氣缸－進排氣單向閥組件運動形式相同，方向正好相反。因此，偏心驅動軸轉動一圈，真空泵完成兩次抽、排氣過程。在電機帶動下，真空泵連續工作，直到真空助力器伺服氣室內最終達到某一穩定的平衡壓力。

3 往復式真空泵性能計算分析

從車用制動助力性能和能耗的角度出發，本文使用3個指標來評價真空泵性能，即極限真空度、達到指定真空度所需時間和功耗。

3.1 理論模型的假設

往復式真空泵的工作過程相當復雜，在建立往復式真空泵計算模型時，進行如下假設:

a. 常溫下真空泵中工作氣體是稀薄氣體，可近似簡化為理想氣體；氣體壓縮過程指數和膨脹過程指數假設為定值，且均等于絕熱指數。

b. 真空泵工作循環過程中，吸氣壓力與實際排氣壓力均假設為定值。

c. 真空泵吸氣和排氣過程中，氣體溫度恒定。

d. 由于電機轉速很高，活塞副部分的摩擦功耗采用平均功耗計算。真空泵工作受到泄漏、溫度變化、容積效應等因素的影響都反映在抽氣速率這個性能參數上，即通過乘以修正系數來表示這些因素對真空泵性能的影響。

3.2 極限真空度的計算

由于往復式真空泵左、右兩邊活塞副的運動形式一致，因此取一邊的活塞副作為研究對象。當氣缸處于抽氣過程時，進氣單向閥被打開；隨著氣體不斷進入，氣缸中的壓力將不斷減小；當氣缸內體積達到最大時，氣缸內的壓力隨之達到最小；當進氣單向閥左、右兩邊的壓力相等時，進氣單向閥將常閉；此后，不管活塞如何繼續運動，進氣單向閥再也無法打開。當處于排氣過程時，氣缸內氣體的體積被壓縮到最小，壓力達到最大，當排氣單向閥左、右兩邊的壓力相等時，排氣單向閥自行關閉；此后無論活塞如何運動，排氣單向閥也無法再次打開。此時，真空泵既不抽氣，也不排氣，真空泵處于動平衡狀態。此時真空助力器伺服氣室所能達到的壓力稱為真空泵的極限壓力，對應的真空度稱為真空泵的極限真空度。

活塞運動到達主軸側的極限位置稱為內止點，活塞運動到達遠離主軸側的極限位置稱為外止點，活塞從內止點運動到外止點，掃過的體積為氣缸的工作容積Vs。當真空泵處于平衡狀態時，設定活塞在內止點時氣缸內的壓力為Pin，真空助力器伺服氣室的極限壓力為Plimt，頂開進氣單向閥所需的壓力為Piv。

如圖2a所示，進氣單向閥左、右壓力平衡，有：

活塞從內止點運動到外止點時，活塞頂部到進氣單向閥座的體積為氣缸的余隙容積Vc。在動平衡狀態下，設活塞在外止點時氣缸內的壓力為Pout，大氣壓力為P0，頂開排氣單向閥所需的壓力為Pev。

如圖2b所示，則有：

動平衡狀態下，進氣單向閥和排氣單向閥都是常閉的，根據氣體守恒定律，可得：

聯立式（1）～式（3），可得 Plimt為：

真空泵的極限真空壓力Pvac_limt和極限真空度λlimt分別為：

3.3 到達指定真空度所需時間的計算

真空泵理論抽氣速率St為[1]：

式中，D為氣缸直徑；H為活塞行程；n為曲軸轉速；i為工作氣缸數目。

在實際情況下，真空泵的抽氣過程由于泄漏、進氣閥和管道阻力損失、溫度、氣流脈動、容積效應等因素的影響，實際吸氣量會減少，其實際抽氣速率Sd可表示為：

式中，η為抽氣效率，計算公式為：

式中，ηV為相對容積系數，按經驗取 0.85～0.95；ηP為吸氣壓力系數，按經驗取0.8～0.85；ηT為吸氣溫度系數，按經驗取0.97～0.99；ηL為泄漏系數，按經驗取0.85～0.95[1]。

假定排氣過程氣體溫度不變，在dt時間內，真空泵所抽取的氣體量為PSd·dt。但由于Vc的存在，每次排氣過程都無法把氣缸內所有的氣體排凈，因此每次抽氣時氣缸內有殘余氣體，設由Vc引起單位時間返回伺服氣室內的氣體量為QB。

由伺服氣室內氣體量的凈減量 QB·dt－PSd·dt引起伺服氣室的壓力變化dP，因而可以得出真空系統的排氣狀態微分方程[6]：

式中，Vh為真空助力器伺服氣室的容積。

根據初始條件，當t=0時，伺服氣室內的初始壓力為Pc；當 t→∞時，真空泵達到平衡狀態，真空助力器伺服氣室內壓力為恒定值，則P∞=QB/Sd。

根據公式（4）可知：

即可得到QB：

將式（12）代入式（10），并對排氣狀態微分方程（10）兩邊進行積分，可得出抽氣速率與壓力的關系：

由于真空度與壓力的關系為：

若指定真空助力器伺服氣室內的真空度為λ，根據公式（13）、（14）可以計算出所需的抽氣時間t:

3.4 功耗的計算

3.4.1 絕熱循環功耗和氣閥損失功耗計算

圖 3為真空泵的示功圖，4－1－2－3為理論循環過程。在實際循環過程中，由于真空泵存在余隙容積、流動阻力、氣體泄漏、熱交換及壓力脈沖等因素的影響，使得實際進氣壓力Ps′低于理論進氣壓力Ps，實際排氣壓力Pd′高于理論排氣壓力Pd，即真空泵實際循環過程如圖 3 中曲線 4′－1′－2′－3′所示。 其中，曲線 4′－1′代表抽氣過程，氣體不斷進入氣缸；1′－2′為壓縮過程，活塞運動壓縮缸內氣體；2′－3′為排氣過程，氣體受到活塞的推擠而排出氣缸；3′－4′為膨脹過程，即氣缸內剩余氣體的膨脹。

真空泵實際循環絕熱功即為面積 4′－1′－2′－3′－4′，為了計算方便也可以認為是面積 1′－2′－5′－6′－1′與面積 4′－3′－5′－6′－4′之差，即：

式中，V1′－2′（P）、V3′－4′（P）分別表示壓縮過程和膨脹過程氣缸容積與壓力的函數關系。

假定壓縮過程指數與膨脹過程指數相等，且都等于絕熱過程指數，按照力學氣體狀態方程[7]，多變過程方程為：

式中，m為絕熱過程指數；V1′代表實際抽氣終了時刻1′處對應的氣缸體積。

則 1′-2′－5′－6′－1′所圍的面積為：

同理可求得 4′－3′－5′－6′－4′所圍的面積：

式中，V4′代表實際膨脹終了時刻4′處對應的氣缸體積。

聯立公式（16）、公式（18）和公式（19），真空泵循環絕熱功為：

式中， 實際進氣壓力 Ps′=Ps-ΔPs，ΔPs為進氣壓力損失；實際排氣壓力 Pd′=Pd+ΔPd，ΔPd為排氣壓力損失；氣缸實際的工作容積 Vs′=V1′－V4′。

在實 際循 環過 程中 ，Ps與 Ps′、Vs與 Vs′相 差很小，可近似認為：

將式（21）代入式（20）得：

令δs=ΔPs/Ps為進氣閥平均相對壓力損失，δP=ΔPd/Pd為排氣閥平均相對壓力損失，則考慮氣閥損失和絕熱循環的真空泵功耗為：

3.4.2 摩擦功耗計算

真空泵工作時，其摩擦功耗有很大一部分由缸體－活塞環摩擦副引起，對單個活塞缸，活塞環與缸體間的摩擦力Ff為：

式中，μ為摩擦因數；FN為活塞環張力。

由于電機的轉速快，活塞的速度變化快，因此在計算時考慮摩擦副的平均功耗，活塞運動的平均速度Vm為：

式中，S為活塞行程；n為曲軸轉速。

則整個真空泵摩擦力的功耗為：

3.4.3 總功耗計算

綜合考慮絕熱狀態變化的功耗、進排氣閥的壓力損失功耗和活塞副的摩擦功耗，真空泵總功耗為:

但由于真空泵有曲軸連桿等傳動部件以及各密封件之間的摩擦損失，若把除缸體－活塞環摩擦副外的摩擦件傳動損失均考慮在機械效率ηm內，則ηm通常取0.7～0.85。另外，真空泵由電機帶動，需要考慮電機效率 ηe，ηe一般可取 0.80～0.85。此外，真空泵的內泄漏、冷卻溫度、運動負荷波動、吸氣狀態突變等因素難以用數值關系表示，可參考往復式壓縮機，采用修正系數將真空泵功耗增加5%～15%[6]。

因此，往復式真空泵電機的功耗可表示為：

4 真空泵性能實測及計算結果對比分析

真空泵性能測試試驗臺如圖4所示，通過抽氣泵P1、電磁閥V1和V2調節抽氣容器壓力，確定測試時抽氣容器的初始壓力；利用抽氣泵P2和電磁閥V3調節壓力模擬氣室的氣壓,以模擬真空泵在高原、平地等不同工作環境下的氣壓。

真空泵與抽氣容器、壓力模擬氣室之間用真空軟管連接，并由試驗臺向電機提供12V的工作電壓。真空泵性能的測試過程如下：關閉電磁閥V1，利用抽氣泵P1對抽氣容器進行抽氣，直至抽氣容器內的壓力達到設定的初始壓力，關閉電磁閥V2；關閉電磁閥V3和V4，通過抽氣泵P2對壓力模擬氣室進行抽氣，使氣室內的壓力達到模擬的環境壓力；打開電磁閥V4開始測試。壓力傳感器S1與抽氣容器相連，壓力傳感器S2與壓力模擬氣室相連，通過壓力傳感器S1、S2測得不同時刻抽氣容器內和壓力模擬氣室內的壓力值，然后將對應時刻的壓力值轉化為0～5V的線性電信號，電腦通過采集0～5V的電信號，并且利用公式（13）將壓力值換算成真空度，即可以得到對應時刻的真空度值。

表1為往復式真空泵測試時的環境參數、工作參數和幾何參數，根據這些參數調整試驗設備，運用上述計算分析方法仿真計算該真空泵的性能指標。

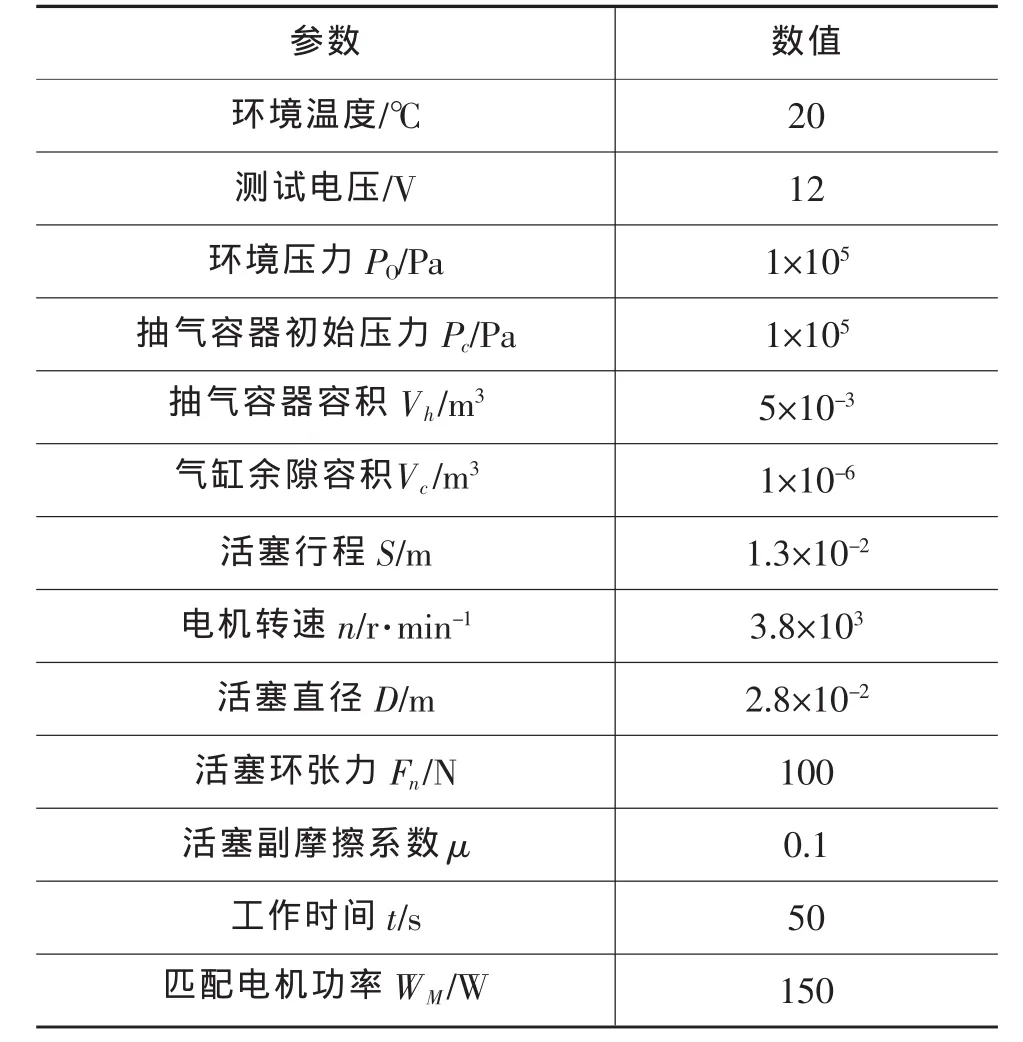
表1 往復式真空泵測試時參數

4.1 極限真空度的對比分析

通過試驗測試出來的極限真空度為0.8421，計算得到的極限真空度為0.8658，相對誤差為2.814%，在誤差范圍5%之內，即該計算分析方法具有一定的計算精度與可行性。

4.2 達到指定真空度所需時間對比分析

根據測試數據與計算數據繪制真空度與時間的關系曲線如圖5所示，可以比較理論計算和實際測試真空助力器伺服氣室達到不同真空度所需的時間。

由圖5可以看出，測試曲線與計算曲線較為吻合，真空度為0.5時，計算時間為4.472 6 s，測試時間為4.641 s，相對誤差為3.629%；真空度為0.7時，計算時間為8.6076s，測試時間為8.9452s，相對誤差為3.009%；真空度為0.8時，計算時間為13.3333 s，測試時間為14.683 5 s，相對誤差為9.195%。可以看出，達到指定真空度所需的時間計算值和測試值相近。

4.3 真空泵功耗的對比分析

根據真空泵功耗計算公式，取機械效率為70%，電機效率為80%，修正系數為1.05，計算得到真空泵的功耗為150.34 W。對比該往復式真空泵匹配的電機功率為150 W，相對誤差為0.2%。因此，可以根據本文功耗的計算方法選擇與真空泵所匹配的電機。

5 結束語

闡述了往復式真空泵的結構及其工作原理，并提出了真空泵的性能評價標準，對往復式真空泵的極限真空度、達到指定真空度所需的時間以及真空泵功耗3個性能指標進行了分析。通過試驗驗證可以看出，試驗結果與計算結果誤差范圍基本在5%之內，由此證明該計算分析方法具有較高的計算精度，能為今后車用往復式真空泵進一步的設計計算提供理論依據。

1 A.Chambers，R.K.Fitch，B.S.Halliday.Basic vacuum technology.Institute of Physics Pub,1998.

2 Yu Su， Ta－i Sawada， Jun－ichi Takemoto， Shuji Haga.Theoretical study on the pumping mechanism of a dry scroll vacuum pump.Vacuum，1996，47:815～818.

3 M.H.Hablanian.Design and performance of oil－free pumps.Vacuum，1990，41:1814～1818.

4 R Mathes，JP Périn.Vacuum performances of molecular and turbomolecular pumping stages at low temperature.Vacuum，1996，47：779～782.

5 徐成海，等.真空工程技術.北京：化學工業出版社，2006.

6 王欲知，陳旭.真空技術.北京：北京航空航天大學出版社，2007.

7 林梅，吳業正.壓縮機自動閥.西安:西安交通大學出版社，1991.

8 索得爾[美].壓縮機氣閥設計與力學原理.王迪生，譯.西安:西安交通大學出版社，1998.

9 林逸,賀文娟，何洪文，陳瀟凱.電動汽車真空助力制動系統的計算研究.汽車技術，2006，10：19～22.