天然腸衣搭配的數學優化模型

吳甬翔，金 敬

（寧波職業技術學院 公共教學部，浙江 寧波 315800）

天然腸衣搭配的數學優化模型

吳甬翔，金 敬

（寧波職業技術學院 公共教學部，浙江 寧波 315800）

[摘 要]以2011年高教社杯全國大學生數學建模競賽賽題為背景，針對天然腸衣搭配問題，利用LINGO軟件，建立關于天然腸衣組裝成品捆數最多的線性規劃模型和對應的原料搭配方案數學模型，求出各規格模型的最優解，提供各規格原料的具體搭配方案，使資源分配得到最優化，企業效益達到最大化。

[關鍵詞]天然腸衣；搭配方案；數學模型；線性規劃；LINGO軟件

1 問題的提出

天然腸衣制作加工是我國一個傳統產業，為提高生產效率，公司計劃改變組裝工藝，先丈量所有原料，建立一個原料表（見表1）；然后根據三種成品規格的要求（見表2），設計一個原料搭配方案，使工人根據這個方案“照方抓藥”進行生產[1]。

公司對天然腸衣搭配方案有以下具體要求[1]：

（1）對于給定的一批原料，裝出的成品捆數越多越好；

（2）對于成品捆數相同的方案，最短長度最長的成品越多，方案越好；

（3）為提高原料使用率，總長度允許有0.5m的誤差，總根數允許比標準少1根；

（4）某種規格對應原料如果出現剩余，可以降級使用。如長度為14m的原料可以和長度介于7～13.5m的原料進行捆扎，成品屬于7～13.5m的規格；

（5）為了食品保鮮，要求在30min內產生方案。

2 問題的分析

針對公司要求，在已知成品規格和原料情況下，設計符合要求的搭配方案，其實質是數學模型優化問題。由于原料出現剩余時可降級使用，為使原料能夠充分利用，可以先把第三規格剩余的原料和第二規格剩余的原料拼在一起，按第二規格的要求建立模型進行原料的搭配，求出可以搭配的成品捆數。如果仍有剩余，則把剩余的原料和第一規格剩余的原料拼在一起，按第一規格的要求建立模型進行原料的搭配，求出可以搭配的成品捆數。因此，如何設計最優的搭配方案使原料按照三種成品規格進行組裝,得到最多成

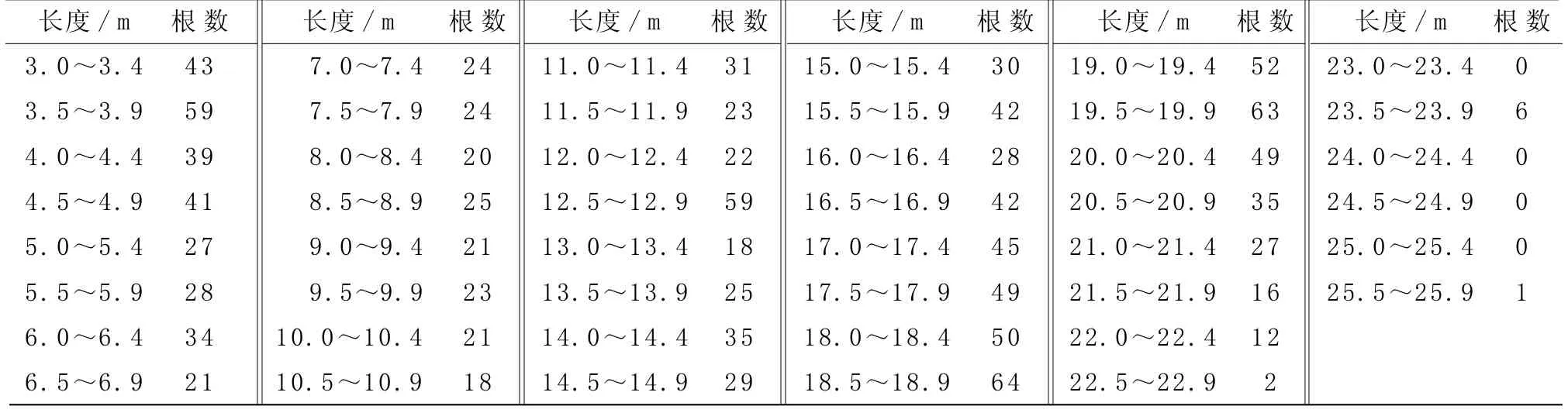
表1 原料描述

表2 成品規格

3 模型假設與符號說明

3.1 模型假設

天然腸衣制作加工的環境有良好通風條件，有適宜溫度；整個原料搭配過程中腸衣沒有受到損壞；生產出來的都是合格的成品腸衣；原料的擺放分類明確，不會出現混淆情況[3]。

3.2 符號說明

F表示成品捆數；f1，f2，f3分別為第一規格搭配的成品捆數、第二規格搭配的成品捆數、第三規格搭配的成品捆數；ai（i=1，2，3，…，8）表示3～6.5m中每檔原有根數；bj（j=1，2，3，…，14）表示7～13.5m中每檔原有根數；ck（k=1，2，3，…，24）表示14～25.5m中每檔原有根數；xi（i=1，2，3，…，8）表示3～6.5m中每檔抽取根數；yj（j=1，2，3，…，14）表示7～13.5m每檔抽取根數；zk（k=1，2，3，…，24）表示14～25.5m每檔抽取根數。

4 模型的建立與求解

4.1 各規格原料組裝成品捆數最多的線性規劃模型

由于要保證每捆長度為89m，為提高原料使用率，每捆總長度允許有±0.5m的誤差，而且總根數允許比標準少1根，因此得到線性規劃模型為：

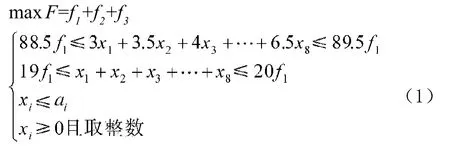
每種規格對應原料如果出現搭配剩余可以降級使用，因此從（3）式開始計算。利用LINGO[4-5]軟件解得第三規格可搭配的成品捆數f3=137，同時得到每檔所需根數為：z1=35，z2=29，z3=30，z4=42，z5=28，z6=42，z7=45，z8=49，z9=50，z10=64，z11=52，z12=63，z13=49，z14=35，z15=27，z16=16，z17=12，z18=2，z19=0，z20=5，z21=0，z22=0，z23=0，z24=1。

定向越野運動不但考驗學生的身體素質，對其綜合能力也是一種考驗。如，在開展定向越野運動時，首先，教師可多設定幾條不同路線，并在不同路線上設置多個不同的目標，路線的選擇與最終的成績相關聯，在這個思考、分析和選擇的過程中，學生的綜合能力也會得到相應的鍛煉與提高。其次，教師可在地圖上設置一些陷阱目標，從而鍛煉學生的分析能力、選擇能力和決斷能力，這對學生未來的發展具有積極意義。

與原料表相比較，z20（檔次為23.5～23.9m）剩余1根。把z20剩余的一根降級到第二規格進行搭配，利用LINGO軟件解得第二規格可搭配的成品捆數f2=37，同時得到每檔所需根數y1=0，y2=6，y3=4，y4=25，y5=21，y6=23，y7=21，y8=18，y9=31，y10=23，y11=22，y12=59，y13=18，y14=25，y20=0。y1（檔次為7～7.4m），y2（檔次為7.5～7.9m），y3（檔次為8～8.4m），z20（檔次為23.5～23.9m）分別剩余24、18、16、1根。再把剩余根數降級到第一規格進行搭配，利用LINGO軟件解得第一規格可搭配的成品捆數f1=16，同時得到每檔所需根數x1=43，x2=59，x3=39，x4=41，x5=27，x6=28，x7=34，x8=20，y1=19，y2=0，y3=0，z20=0。x8（檔次為6.5～6.9m），y1（檔次為7～7.4m），y2（檔次為7.5～7.9m），y3（檔次為8～8.4m），z20（檔次為23.5～23.9m）分別剩余1、5、18、16、1根。最后將剩余根數進行檢驗，分別按第一、二規格運算，經過驗證無解，則不可再搭配成捆。因此，天然腸衣組裝成品捆數最多為max F=f1+f2+f3=16+37 +137=190。

4.2 各規格原料搭配的數學模型

根據天然腸衣最多組裝的成品捆數，利用線性方程組，建立各規格原料搭配的數學模型。

第一規格每捆原料搭配的數學模型為：

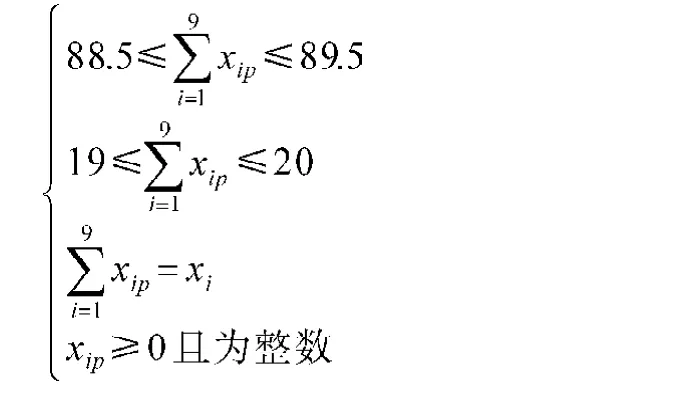
其中，xip表示從每捆每檔中抽取的根數，p表示第幾捆（i=1，2，3，…，9；p=1，2，3，…，16）。利用LINGO軟件計算得到第一規格原料搭配方案（見表3）。

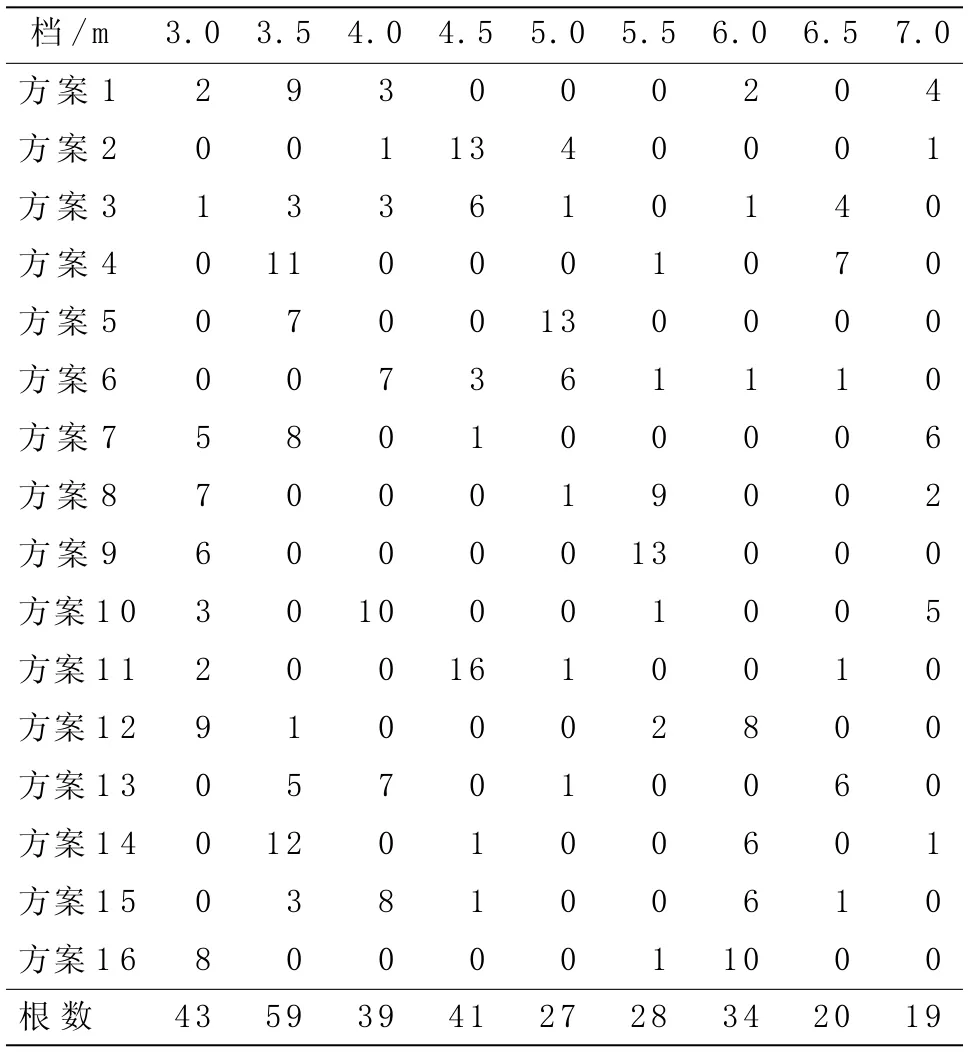
表3 第一規格原料搭配方案

第二規格每捆原料搭配的數學模型為：

第三規格每捆原料搭配的數學模型為：

其中，zkg表示從每捆每檔中抽取的根數，g表示第幾捆（k=1，2，3，…，24；g=1，2，3，…，137）。利用LINGO軟件計算得到第三規格原料搭配方案（見表5）。

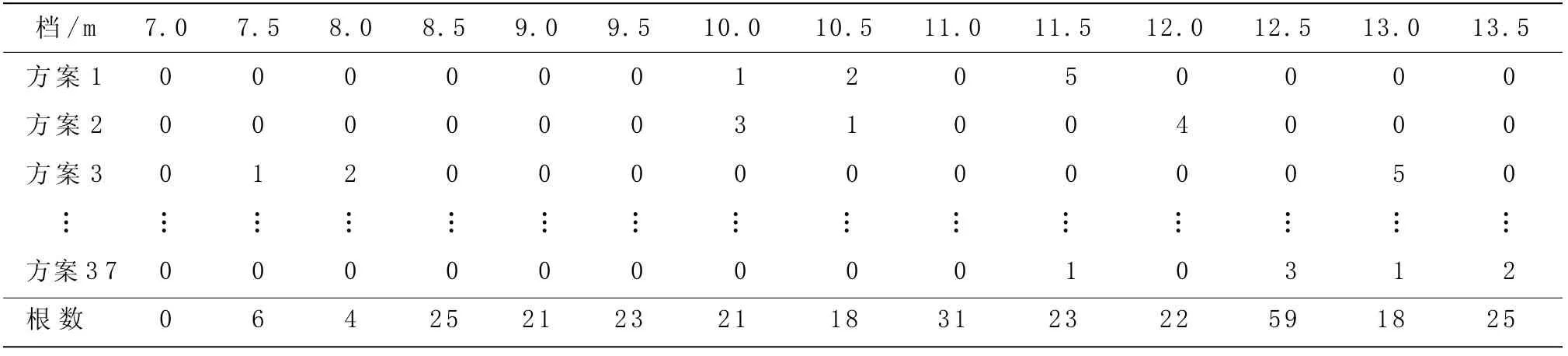
表4 第二規格原料搭配方案

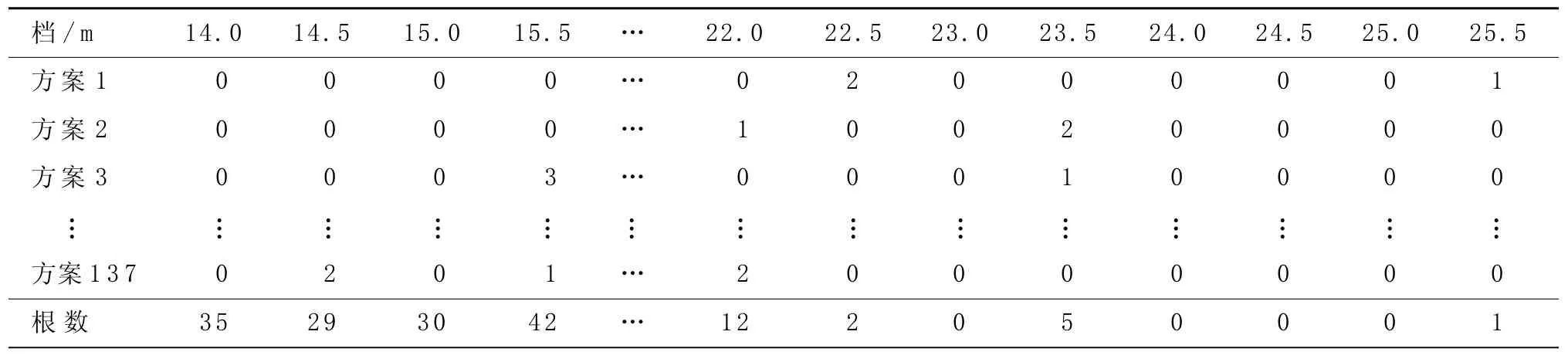
表5 第三規格原料搭配方案

5 結 論

按照公司對天然腸衣搭配方案的具體要求，先丈量所有原料，建立原料表，然后采用線性規劃模型和數學優化模型，利用LINGO軟件計算即可得到三種規格原料的具體搭配方案，這可以使工人根據最優方案“照方抓藥”進行生產，節省時間，滿足30min產生方案的要求。該數學優化模型研究的是生產加工過程中分揀組裝的實際問題。通過利用LINGO軟件，可以降低計算難度，提高工作效率，準確快速地得出合理優化的搭配方案。對于生產過程中原料損耗等問題，一些參數可以依據實際情況而設定。因此，該數學優化模型對于提高工作效率和生產效率具有普遍性和實用性。

[參 考 文 獻]

[1]中國工業與應用數學學會.2011年高教社杯全國大學生數學建模競賽賽題[EB/OL].(2011-09-09)[2012-09-15]. http://www.mcm.edu.cn/html_cn/node/a1ffc4c5587c8a6f96eacefb8dbcc34e.html.

[2]石國春，唐玉鵬，王鵬飛，等.天然腸衣搭配問題[J].蘭州工業高等專科學校學報，2012，19(3):60-63.

[3]中國天然腸衣出口指南[EB/OL].(2005-02-19)[2012-09-15].http://wenku.baidu.com/view/0c3fcf80e53a580216fcfe21.html.

[4]試鋒芒.Lindo&Lingo教程[EB/OL].(2010-04-30)[2012-09-15].http://wenku.baidu.com/view/f7149dc24028915f804dc22b.html.

[5]謝金星，薛毅.優化建模與LINGO/LINGO軟件[M].北京:清華大學出版社，2005:11-15.

[責任編輯：宣 明]

[中圖分類號]O224

[文獻標識碼]A

[文章編號]1671-4326(2012)04-0048-03

[收稿日期]2012-09-26

[作者簡介]吳甬翔（1976—），女，浙江寧波人，寧波職業技術學院公共教學部講師；金 敬（1968—），女，浙江寧波人，寧波職業技術學院公共教學部講師.品捆數，是解決該問題的關鍵。通過利用線性規劃模型和數學優化模型，建立目標函數，結合LINGO軟件求出各規格模型的最優解[2]。

Mathematical Optimization Model of Natural Casing Match

WU Yongxiang, JIN Jing
(Public Courses Department, Ningbo Vocational and Technical College, Ningbo, 315800, China)

Abstract:On the background of 2011 National College Mathematical Modeling Contest of Higher Education Cup, a linear programming model with the most finished bundle number of natural casing and a corresponding mathematical model of material matching scheme are set up in terms of the match problem of the natural casing by using the LINGO software. The purpose is to work out the best solution to various models and provide the specific matching scheme to obtain the optimization both in the source allocation and the company benefit.

Key words:Natural casing; Matching scheme; Mathematical model; Linear programming; LINGO software