基于混合整數規劃的高級計劃排程方法研究
李海寧,孫樹棟,郭 杰
(西北工業大學 機電學院,西安 710072)
0 引言
目前,國內大型離散制造企業一般采用企業級物料需求計劃(MRP)和車間級生產調度(scheduling)的兩層計劃編制模式。由于MRP是一類粗粒度的需求計劃,其忽略了車間實際的制造能力和零部件加工進度等約束,使得車間生產所依賴的數據源頭存在不合理性,從而導致車間計劃調度、零部件加工、生產準備等一系列生產組織活動陷入被動和混亂。
高級計劃排程 (Advanced Planning and Scheduling,APS) 是一種基于供應鏈管理和約束理論的先進計劃與排產工具。Marriott研究了鋼鐵工業供應鏈中的APS系統以改進產品質量、產品收益率和設備效率[1];Romero研究了批量化學加工行業中和財務管理有關的計劃和排程問題[2]。徐曉芳等對APS的發展歷史、功能優勢及特點進行了剖析[3];劉海江等將APS與傳統的CRP能力需求計劃進行了對比,歸納總結了APS相對于傳統能力需求計劃的特點[4];肖牧山等提出了基于TOC理念和DBR模型的APS系統與ERP集成的解決方案,并給出了APS與ERP集成的潛在問題和可行方案[5]。
從上述APS的應用和研究方面分析,目前APS主要應用于供應鏈層次,而在企業層次、車間層次的應用較少;國內對APS的研究主要集中在APS的理念、功能和集成等方面,而在APS的模型和算法求解方面的研究甚少。
本文采用混合整數規劃(Mixed Integer Programming,MIP)這類精確型的數學建模方法,以訂單或生產任務的準時交付為目標,在考慮產品BOM、零件加工順序約束、機器加工能力、訂單提前/拖期等因素的基礎上,構建基于MIP的APS數學模型,并采用遺傳算法(Genetic Algorithm, GA)進行APS模型求解,最后通過算例驗證模型和方法的有效性。
1 基于混合整數規劃的APS模型
1.1 APS模型的假設條件
1)一批零件投入加工后,承制機器的加工期間不能中斷;
2)機器在某一時刻只能加工一個零件;
3)一批零件在機器上加工需要考慮生產準備時間;
4)零件在機器上的加工時間已知,且為確定值;
5)訂單的BOM結構已知,且零件內部的工藝路線依據父子項依次展開。
1.2 參數和變量說明
1)與訂單相關的參數和變量
Oi:訂單(i=1, 2, !,n),其中:n為訂單數量;
Qi:訂單Oi包含的最終產品數量;
Pi:訂單Oi對應的最終產品;
Nip:Pi包含零部件p的結構數量;
Di:訂單Oi的交貨期;
Ci:訂單Oi的完工時間;
Ti:訂單Oi的拖期天數;
Ei:訂單Oi的提前天數;
e:訂單提前的每天懲罰系數;
t:訂單拖期的每天懲罰系數;
A(p):零部件p的所有子項零件集合;
B:無子項的零件集合。
2)與機器相關的參數和變量
Mk:機器(k=1, 2, !,m),其中:m為機器數量;
rk:Mk的準備時間;
Sipk:訂單Oi所屬零件p在機器Mk上的開工時間;
tipk:訂單Oi所屬零件p在機器Mk上的加工時間;
Xip_jq_k:訂單Oi所屬零件p和訂單Oj所屬零件q都在機器Mk上加工,若p在q之前加工,則Xip_jq_k=1,否則為0。
1.3 基于MIP的APS模型
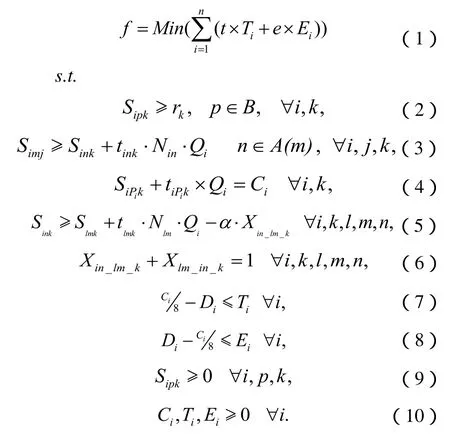
其中:
1)公式(1)為目標函數,即所有訂單的提前/拖期懲罰總成本最小;
2)公式(2)為機器在生產準備完成后才開始加工;
3)公式(3)為產品BOM中父子零件的加工順序約束,即:父項零件的開工時間不能小于其子項零件的開工時間與其加工時間之和;
4)公式(5)和(6)表示同一機器在某一時刻只能加工一個零件;
5)公式(7)和(8)分別為訂單拖期天數和訂單提前天數。這里假設機器每天工作時間為8小時,且天數采用四舍五入的取整方式;
6)公式(9)和(10)限定零部件開工時間、訂單完工時間、拖期量、提前量均為正數。
2 基于遺傳算法的APS模型求解
由于遺傳算法所固有的全局搜索與收斂特性,其得到的次優解往往優于傳統方法得到的局部極值解, 且該算法的搜索效率較高。因此, 本文采用遺傳算法對上述APS模型進行求解。
2.1 染色體編碼與解碼操作
1)基于隨機鍵的編碼方法
為了表示不同零件的先后加工順序和增加染色體的多樣性,采用文獻[6]提出的隨機鍵編碼方式。對于n個待加工零件而言,其對應的染色體的碼長為n,每個零件對應一個0-1之間的小數。這些小數可以看作一組有序的鍵值,鍵值越小,則表示零件加工的優先級越高。例如:若n=5,則(0.1576, 0.9706, 0.9572, 0.4854, 0.8003)就表示一個染色體。
2)染色體解碼方法
對于尚未加工且無子項零件的零部件,或者具有子項零件且其子項零件已經加工完成的零部件,形成一個待加工的零部件集合。依據染色體中各基因位的鍵值大小進行排序,優先安排鍵值較小的零部件優先開工,而零部件的開工時間則取值為它的所有子項零件中的最晚完工時間和機器最早可加工時間的較大值。
2.2 適應度函數
為避免遺傳算法的早熟和隨機漫游現象,需要對目標函數值進行適當放大或縮小來獲得適應度值。在上述APS模型中,目標函數是最小化提前/拖期總懲罰成本,因此,適應度函數確定為:f'=a/f,其中a取值為0.5。
2.3 基于輪盤賭的選擇操作
采用文獻[7]提出的基于輪盤賭的比例選擇法,以促使適應度值較高的染色體以較大概率被選擇到下一代;為了提高遺傳算法的優化效果和收斂性,采用精英保留策略[7],以確保當前種群中最好的染色體直接參與下一代種群的遺傳操作。
2.4 兩點交叉操作
采用如下的兩點交叉操作方法。圖1為兩點交叉操作的示意圖,其中交叉概率設為0.6。
1)隨機兩兩配對生成N/2對染色體,其中N為種群規模;
2)從N/2對染色體中隨機選取一對染色體(P1,P2)作為父代個體;
3)依據隨機鍵編碼方法重新產生一個染色體,確定其小于交叉概率Pc的基因位,互換染色體對(P1,P2)中相應的基因位,生成臨時染色體對(T1, T2)。
4)計算臨時染色體T1和T2的個體適應度值,分別與父代染色體P1和P2的個體適應度值進行比較,保留適應度值較小的兩個染色體作為交叉之后的子代個體。
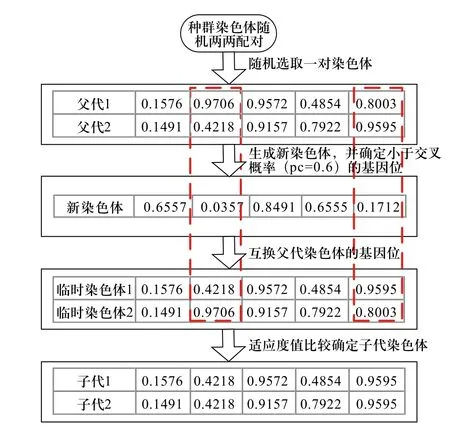
圖1 染色體交叉操作示意圖
2.5 變異操作
變異操作方法為:設變異概率為pm,對種群中的任一染色體Vi(i=1, 2, !,N),隨機產生(0, 1)內的實數r,若r<pm,則依據隨機鍵編碼方法重新產生一個新染色體Vi'來替換Vi,否則,依次對下一染色體執行上述操作。
3 算例仿真
3.1 APS算例
考慮到APS算例的代表性和通用性,本文構造了如圖2所示的具有四級裝配關系的APS算例。在圖2中:既有最終產品F1和F2,同時也包含多個公用零部件,弧線上的數字表示子項零部件的結構數量;另外,部件S4內的零件C13包含兩道加工工序(P1, P2),這里將這兩道工序視為具有先后加工順序的兩個子零件,即C13P1和C13P2。
表1為包含最終產品F1和F2、部件S1、公用零件C2和C3的5個訂單信息,表2為各機器的加工準備時間,表3為各零件、部件和最終產品所需的加工機器及其加工時間(單位:小時)。算例中5臺機器的加工能力為8h/天,訂單的提前懲罰系數為50元/天,訂單的拖期懲罰系數為250元/天。

表1 訂單信息

表2 各機器的準備時間
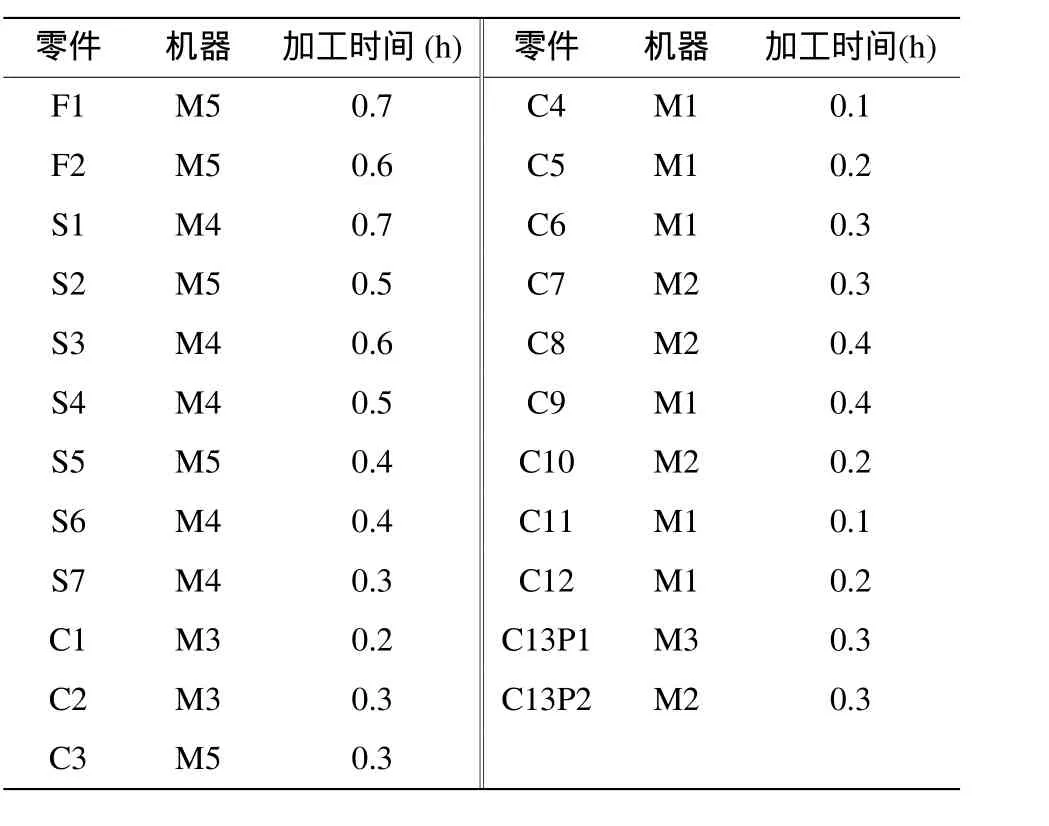
表3 零件的承制機器和加工時間
3.2 仿真結果
遺傳算法參數設置為:種群規模為50,進化代數1000次,交叉概率0.6,變異概率0.1,算法終止條件為進化代數。表4為各訂單交貨期的計算結果,圖3、圖4分別為目標值收斂曲線和APS算例甘特圖。圖4中各塊上的符號表示某一訂單內的零件編號,如“O1S3C2”表示訂單O1內組合件S3下的C2零件。

圖2 產品結構圖
從表3和圖4中可以看出:5個訂單中,只有訂單O2提前一天完工,其他4個訂單都是準時完工,因此,APS的目標函數值(即:提前/拖期總懲罰成本)為50元。另外,從圖3得知,算法在迭代到158代時達到最優目標值。
4 結論
本文針對高級計劃排程問題,以訂單的提前/拖期總懲罰成本最小為目標函數,構建了包含BOM結構、零件加工次序、機器能力約束等的APS混合整數規劃模型;采用遺傳算法對APS模型進行求解,該遺傳算法采用隨機鍵編碼方式、輪盤賭選擇方法、兩點交叉操作、精英保留策略等方法;最后采用算例驗證了APS模型和GA算法的有效性。本文提出的APS建模和求解算法具有一定的通用性,它適用于機械加工企業的生產計劃編制,以及帶有組合件生產任務的作業車間計劃調度。

表4 訂單交貨期仿真結果
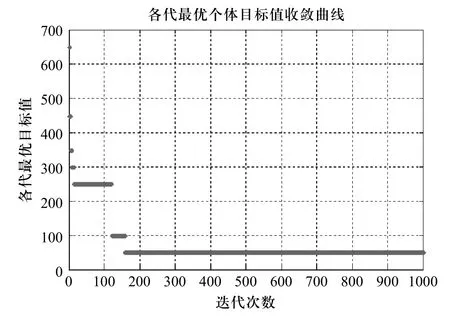
圖3 目標值收斂曲線

圖4 APS算例仿真結果
[1] Marriott P., et al. Advanced production planning as the core element of a supply chain [J]. MPT Metallurgical Plant and Technology International, 2002, 25(1): 78-82.
[2] Romero J., et al. Integrating Budgeting Models into Scheduling and Planning Models for the Chemical Batch Industry[J]. Industrial and Engineering Chemistry Research, 2003, 42(24): 6125-6134.
[3] 徐曉芳, 張偉, 葉春明. APS剖析[J]. 計算機輔助設計與制造, 2002, (4): 13-17.
[4] 劉海江, 汪進. APS與傳統CRP的能力需求分析比較[J].機械設計與制造, 2008, (10): 63-65.
[5] 肖牧山, 魯礫. 基于APS與ERP集成的新型ERP/APS/MES企業管理系統[J]. 企業技術開發, 2008, (9): 15-18.
[6] Bean J C. Genetic Algorithms and Random Key s for Sequencing and Optimization [J]. ORSA Journal on Computing, 1994, 6(2): 154-159.

