含單空位的(10,10)碳納米管的振動性質和拉曼譜

常 旭， 劉獻凱， 吳 攀

(商丘師范學院 物理與電氣信息學院 河南 商丘 476000)

0 引言

單壁碳納米管(SWCNT)是由單層石墨片卷曲而成的一種管狀結構[1]，它擁有很多獨特的電學、光學、熱學和機械性質[2-3]，因此，碳納米管(簡稱為碳管)在理論和實驗上都得到了廣泛的關注.其中，人們對碳管的晶格動力學性質做了大量的研究，并且發現碳管的振動性質和碳管自身的結構緊密聯系[4].對于完整碳管，徑向呼吸模的頻率幾乎與碳管的螺旋度無關，而是與管徑成反比，在這些模式中，相鄰兩個碳原子的振動是同相的.高頻振動模式中，相鄰原子的振動是反相的，并且均平行于碳管的表面，這些模式對碳管的局部結構比較敏感[5-6].而在實際中碳管經常是不完整的，往往包含了各種類型的缺陷，例如Stone-Wales缺陷(簡稱為SW)[7]、單空位(monovacancy，MV)[8]、 雙空位(divacancy, DV)[9]以及這些缺陷的衍生結構[10].當這些缺陷存在時，即使其濃度很小，也會極大地影響碳管的物理和化學性質[11].因此，深入了解缺陷存在時對碳管性質的影響，具有十分重要的意義.

到目前為止，人們對于包含缺陷的碳管的研究，主要集中在缺陷對碳管的結構和電學性質的影響上，著重討論缺陷對碳管中電子輸運性質的改變，這些研究為碳管在量子線和場效應管等方面的潛在應用提供了理論依據[11].同時，這些缺陷無疑也會影響碳管的振動性質.另一方面，拉曼譜可以用來探測碳管的幾何結構，Wu等[7]曾經計算了碳管內分子結的非共振拉曼譜，借此可以在實驗上探測碳管分子結的存在，其理論結果得到了聚焦拉曼譜成像實驗的支持[12].振動性質時常被用于研究材料的結構特征，例如， Miyamoto等[13]利用密度泛函理論計算了包含有SW缺陷的(3, 3)碳管的特征聲子模式；實驗上則利用振動特性來區分氮化硅中的氮空位[14].2008年，文獻[15-16]分別利用密度泛函理論和緊束縛近似的方法，計算了含有單空位的zigzag管的聲子頻率.然而，對于含有單空位的armchair管的振動性質以及相關的拉曼譜特征尚未被系統地研究.

作者將以(10, 10)碳管為例，利用晶格動力學方法，探討含有單空位的armchair碳管的振動特性以及單空位存在時對碳管非共振拉曼譜的影響.

1 計算模型和方法

選擇了包含5個平移元胞的(10, 10)碳管，其軸向長度為1.231 nm，且在管軸方向利用了周期性邊界條件.使用經驗的Brenner勢函數描述碳原子之間的相互作用[17].利用晶格動力學方法計算碳原子之間的力常數和振動模式，力常數矩陣元可以表示為

(1)

其中，i和j表示不同的碳原子，l和m為元胞指標，α和β表示三維笛卡爾坐標x,y,z.

采用數學上常用的BFGS優化方法對碳管進行結構優化[18]，當原子間的力小于1.0×10-6eV/nm時，即認為系統達到最穩定的狀態.對該狀態下的力常數矩陣進行傅里葉變換即可以得到動力學矩陣，再將動力學矩陣對角化并求解久期方程，就可以得到所有的振動模式.需要說明的是，在下面的拉曼譜計算中，為了滿足光子和聲子的動量守恒，只有波矢k=0的聲子能與入射光耦合，所以在這里僅僅需要計算布里淵區中Γ點的聲子模式[5].以振動頻率和振動模式為基礎，接下來利用經驗鍵極化模型計算碳管的非共振拉曼譜[19].

2 結果與討論

實驗表明，當用粒子轟擊碳管表面時，有可能使碳原子脫離碳管從而形成單空位，這樣就出現了3個懸掛鍵.通常情況下，這樣的結構是不穩定的，因此，懸掛鍵要重組從而形成新的C—C鍵，最終剩余1個懸掛鍵.于是，單空位經過結構優化之后轉化為五邊形和1個懸掛鍵的復合結構，也就是所謂的“5-1DB”缺陷[9]，如圖1所示,左側箭頭代表管軸方向.碳管中新形成的C—C鍵用黑色著重顯示，并且用“NB”標志，考慮到單空位處新形成的C—C鍵相對于管軸有2種不同的取向，如圖1(a)中，新形成的鍵和管軸方向平行，稱這種構型為“5-1DB-parallel”(簡稱為“5-1DB-p”)；在圖1(b)中，新形成的鍵相對于管軸是傾斜的，稱這種結構為“5-1DB-tilt”(簡稱為“5-1DB-t”).

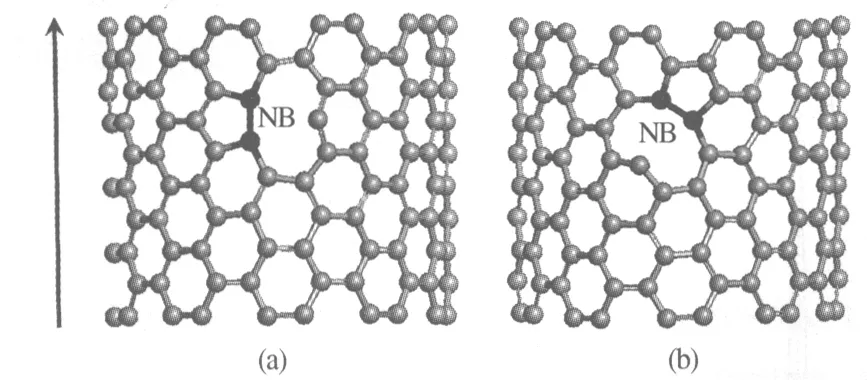
圖1 (10, 10)碳管表面去掉1個碳原子后形成的新結構Fig.1 Schematics for the reconstructed geometrical structures of the defective (10, 10) SWCNT with MV

在計算中，這2種構型都是穩定的.比較了長度為1.231 nm的元胞中包含不同個數的單空位時，2種構型中單空位的形成能的大小，形成能的計算公式[20]為

(2)

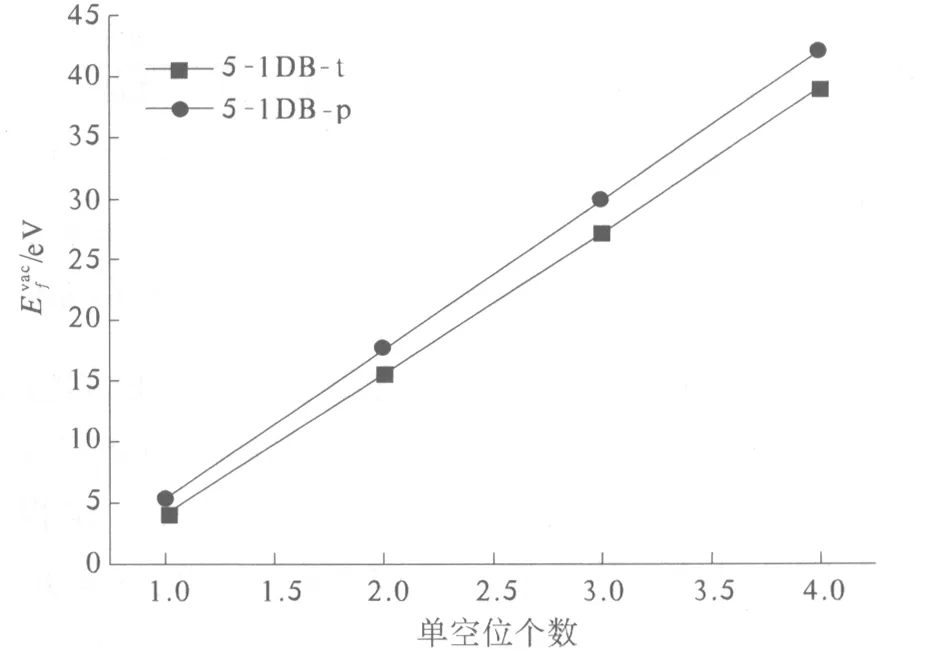
圖2 2種構型下單空位的形成能隨著單空位個數的變化曲線Fig.2 The formation energy of the MVs vs the number of the MVs in the two structures

接下來計算了完整的(10, 10)碳管和包含一個單空位的(10, 10)碳管的聲子譜，如圖3所示.從圖3(a)可以看出，完整碳管的最高頻率在1 700 cm-1左右，這比第一性原理計算的結果要高大約100 cm-1 [21]，這是因為Brenner勢會高估C—C鍵的強度，但是所得結果和緊束縛的計算結果在定量上符合得很好[22].圖3(b)給出了有1個單空位存在時碳管的聲子譜，對比兩圖可以看出，當單空位存在時，高頻區域的頻率發生明顯的藍移，尤其是在1 741 cm-1和1 792 cm-1處出現了2條平帶，猜想這2個振動模式可能對應著單空位，會提供一些關于單空位的信息.

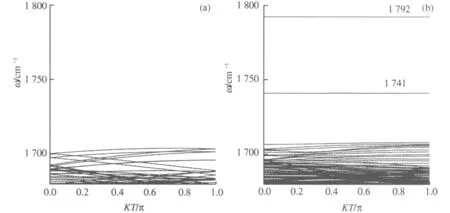
圖3 完整的(10, 10)碳管(a)和包含一個單空位的(10, 10)碳管(b)的聲子譜Fig.3 The phonon dispersion curves for the perfect (10, 10) SWCNT (a) and the defective one (b)

為了進一步研究單空位對碳管振動性質的影響，還計算了完整碳管和包含1個單空位的碳管的非共振拉曼譜，如圖4所示.

圖4 R帶和G帶中含有單空位的(10, 10)碳管的非共振拉曼譜Fig.4 The nonresonant Raman spectra of the defective (10, 10) SWCNT with MV in R-band and G-band

上下兩條曲線分別對應于完整管和單空位的情況.圖4(a)中，虛線代表了完整碳管中徑向呼吸模的頻率位置；圖4(b)中，插入圖代表箭頭所標識處的2個拉曼峰.圖4(b)對應的是高頻區域，首先，相對于完整管的情況，當單空位存在時，高頻G帶發生了一定程度的藍移，并且在G帶劈裂出了更多的峰，猜想這是因為單空位造成的對稱性破缺打破了原有能級的簡并.更為重要的是，在G帶外側出現一些新的峰，并且它們的頻率值和圖3中的2條平帶對應的數值是相同的，從而再次印證了這2個拉曼峰確實可以提供單空位的信息.

圖5 (10, 10)碳管中單空位對應的頻率為1 792 cm-1的特征振動模式Fig.5 The characteristic vibration mode at 1 792 cm-1 of the (10, 10) SWCNT with MV

為了弄清這2個拉曼峰的來源，詳細考察G帶外側這2個峰對應的振動模式，不妨選取相對強度較大的1個拉曼峰，即振動頻率為1 792 cm-1的峰，其振動模式在圖5中給出，圖中箭頭表示空位處原子振動的大小和方向.可以看出，在單空位的周圍，碳原子的振幅最大，并且隨著距空位的距離增大而減小，這意味著該模式正是由單空位帶來的特征模式.猜想其原因如下：高頻拉曼模式對局部C—C鍵的性質非常敏感，特別是鍵長的改變會影響力常數從而間接影響到高頻的振動頻率.在計算中，完整碳管的C—C鍵長是0.145 nm，當單空位存在時，空位周圍的C—C鍵長會發生調整，其中最短的鍵長為0.141 nm，使得這些鍵周圍的力常數要大于完整管的情況，最終在遠離G帶的區域出現了一些新的拉曼峰.因此，可以方便地借助非共振拉曼譜來探測碳管中單空位的信息，這在碳管的結構探測中是很有意義的.

此外關注了R帶的變化情況.從圖4(a)可以看出，當單空位存在時，徑向呼吸模的頻率基本上沒有改變，這意味著碳管管徑幾乎不變.需要指出的是，在計算中單空位的濃度只有0.5%，如果增大單空位的濃度，管徑是否會發生變化，這將在后續工作中加以討論.此外，注意到在徑向呼吸模對應的拉曼峰的兩側劈裂出一些新峰，猜想這是由于空位出現引起了對稱性破缺而造成的.

3 結語

利用經驗的Brenner勢函數描述碳管中碳原子之間的相互作用，討論了包含單空位的(10, 10)碳管的結構穩定性和振動性質，并在此基礎上計算了碳管的非共振拉曼譜.結果發現，單空位存在時，在G帶的外側出現了空位的特征峰，利用這一性質可以探測單空位的存在，這將對實驗有著一定的指導意義.同時，在R帶劈裂出一些小的拉曼峰，這可能源于空位帶來的對稱性破缺.計算結果還表明，在0.5%這樣的低空位濃度下，碳管的管徑幾乎沒有變化.

參考文獻：

[1] Iijima S. Helical microtubules of graphitic carbon [J]. Nature, 1991, 354: 56-58.

[2] Dresselhaus M S, Dresselhaus G, Avouris P. Carbon Nanotubes: Synthesis, Structure, Properties and Applications[M]. Berlin: Springer-Verlag, 2001: 80-84.

[3] 潘立軍，胡行. 碳納米管和硼納米管熱膨脹性能的第一性原理研究[J]. 鄭州大學學報：理學版，2011, 43(2): 83-87.

[4] Dresselhaus M S, Dresselhaus G, Eklund P C. Science of Fullerenes and Carbon Nanotubes [M]. New York: Academic Press, 1996: 32-36.

[5] Saito R, Dresselhaus G, Dresselhaus M S. Physical Properties of Carbon Nanotubes [M]. London: Imperial College Press, 2005: 163-178.

[6] Wu Gang, Zhou Jian, Dong Jinming. Raman modes of the deformed single-wall carbon nanotubes [J]. Phys Rev B, 2005, 72(11): 115411.

[7] Wu Gang, Dong Jinming. Raman characteristic peaks induced by the topological defects of carbon nanotube intramolecular junction [J]. Phys Rev B, 2006, 73(24): 245414.

[8] Rossato J, Baierle R J, Fazzio A, et al. Vacancy formation process in carbon nanotubes: first-principles approach [J]. Nano Lett, 2005, 5(1): 197-200.

[9] Lu Aijiang, Pan Bicai. Nature of single vacancy in achiral carbon nanotubes [J]. Phys Rev Lett, 2004, 92(10): 105504.

[10] Popov V N, Lambin P. Theoretical resonant Raman spectra of nanotube (7, 0) with point defects [J]. Phys Status Solid B, 2009, 246(11/12): 2602-2605.

[11] Biel B, Garcia-Vidal F J, Rubio A, et al. Anderson localization in carbon nanotubes: defect density and temperature effects [J]. Phys Rev Lett, 2005, 95(26): 266801.

[12] Doorn S K, O’Connell M J, Zheng Lianxi, et al. Raman spectral imaging of a carbon nanotube intramolecular junction [J]. Phys Rev Lett, 2005, 94(1): 016802.

[13] Miyamoto Y, Rubio A, Berber S, et al. Spectroscopic characterization of Stone-Wales defects in nanotubes [J]. Phys Rev B, 2004, 69(12): 121413.

[14] Goss J P, Hahn I, Jones R, et al. Vibrational modes and electronic properties of nitrogen defects in silicon [J]. Phys Rev B, 2003,67(4): 045206.

[15] He Huiye, Pan Bicai. Characteristic vibrational modes of a single vacancy in a zigzag carbon nanotube [J]. Phys Rev B, 2008, 77(7): 073410.

[16] Malola S, H?kkinen H, Koskinen P. Raman spectra of single-walled carbon nanotubes with vacancies [J]. Phys Rev B, 2008, 77(15): 155412.

[17] Brenner D W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films [J]. Phys Rev B, 1990, 42(9): 9458-9471.

[18] Liu Dongcai, Nocedal J. On the limited memory BFGS method for large scale optimization [J]. Mathematical Programming B, 1989, 45(5): 503-528.

[19] Wirtz L, Lazzeri M, Mauri F, et al. Raman spectra of BN nanotubes: ab initio and bond-polarizability model calculations [J]. Phys Rev B, 2005, 71(24): 241402.

[20] Gerber I C, Puech P, Gannouni A, et al. Influence of nitrogen doping on the radial breathing mode in carbon nanotubes [J]. Phys Rev B, 2009, 79(7): 075423.

[21] Rao A M, Richter E, Bandow S, et al. Diameter-selective Raman scattering from vibrational modes in carbon nanotubes [J]. Science, 1997, 275(5297): 187-191.

[22] Kahn D, Lu Jianping. Vibrational modes of carbon nanotubes and nanoropes [J]. Phys Rev B, 1999, 60(9): 6535-6540.