中國海島縣經濟測度與綜合實力演變

張耀光

（遼寧師范大學海洋經濟與可持續發展研究中心，遼寧 大連 116029）

產業結構是經濟結構的重要組成部分，它的演進對經濟結構的變化具有較強的表征作用。中囯海島縣自1978年以來經濟有了快速的發展，1980年國內生產總值為12.05億元，人均GDP為473.5元，到2008年國內生產總值達到1 101.4億元，人均GDP達37 017元，分別增長91倍和78.2倍。12個海島縣三次產業構成也有明顯變化（表1），三次產業結構以“二三一”為主，說明海島縣仍處于工業化進程中。其中，漁業實現增加值僅占GDP的12.6%，以漁業生產為主的海島縣也僅有長島縣和長海縣兩個，說明中國海島發展已由依賴海洋生物資源向依賴海洋綜合資源轉變。

1 海島縣產業結構動態灰色關聯模型分析

從12個海島縣三次產業結構圖中（圖1），可以看出產業結構的靜態變化。海島縣的產業結構自1995年以來發生了明顯的變化。2000年之前三次產業的增長速度基本相同，2000年之后隨著海島開發建設的加強，海島縣的第二產業和第三產業增速明顯超過第一產業，特別是2004年以后海島縣第二產業轉變為海島縣的主導產業。第一產業占經濟總產值的比重由1995年的近40%滑落至2008年的20%以下，而海洋第二產業則保持強勁的增長勢頭由原先的20%以下增長到2008年的45%左右，海洋第三產業的發展速度處于第一產業和第二產業之間，所占比重在2000年以后一直穩定在30%以上。

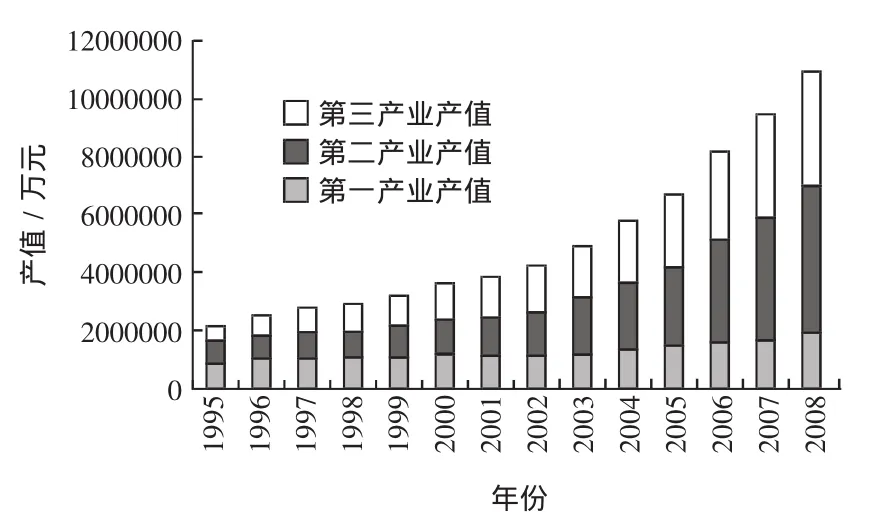
圖1 中國海島縣三次產業構成Fig.1 Composition of three industries in island countries of China

灰色關聯分析（GRA）是某一變化系統的發展態勢的量化分析[1]。它可充分利用已有的白化信息，采用動態的分辨系數反映各因素間的聯系。以12個海島縣的經濟總產值為母序列，子序列分別為一、二、三產業產值。計算母序列與各子序列之間的關系，（子序列之間的關聯度未進行計算）。

關聯系數的計算公式為：

對初值化之后的矩陣按列求均值，即得均值：

若λt=0，即有一列絕對差值全部為0，這時ξ（t）與 ρ的取值無關。

若λt＜1/3，則觀測數據有部分數據波動較大，所以取ρ=1.5λt來減小分辨系數對關聯系數的支配作用。

若1/3＜λt＜1/2，則觀測數據比較平穩，所以可取 ρ=2λt。

若1/2＜λt，則觀測數據更平穩，可取ρ∈（0.8，1]（此種情況，本文計算中均取0.9）。

關聯度是關聯系數的平均值，其表達式為：

上述方法計算得到的關聯度，僅反映某一時段內各因素之間的定量關系，適宜做靜態分析。

從圖2中可以看出，第二產業與海島縣總值的關聯系數起伏比較大，并且一直處于高位，保持在0.6以上，在2000年時接近1。在2002年之前第一產業與經濟總值的關聯系數高于第三產業，2002年之后隨著海洋第三產業的快速發展，第三產業的關聯系數超過了第一產業，在2004年之后三次產業與海島經濟總值的關聯系數趨于一致，說明三次產業向比較協調方向發展。

圖2 中國海島縣海洋三次產業關聯系數變化圖Fig.2 Changes of correlation coefficient of three industries in China′s island counties

但由于不同時段內因素間的關聯關系不盡相同，因此，采用動態關聯度分析法，即把不同時段計算的關聯度按一定順序排列起來。用它可以分析系統內因素之間隨時間而變化的動態關系。通過計算得出動態關聯度矩陣（表1）和動態關聯變化圖（圖 3）。

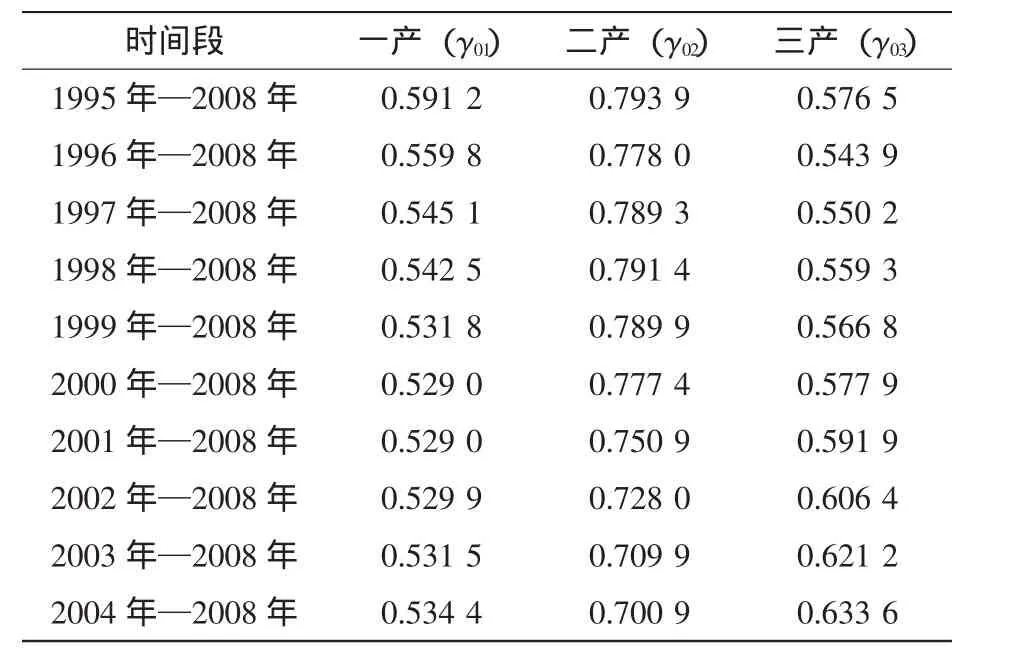
表1 動態關聯度矩陣Tab.1 Dynamic correlation matrix

從圖3中可以看出：（1）三次產業的動態關聯序除了1995年—2008年和1996年—2008年時間段是γ02＞γ01＞γ03，以后各個時間段的關聯序均為 γ02＞ γ03＞ γ01。（2）各關聯度數值中，第二產業動態關聯度明顯高于第一、二產業，保持在0.7以上，說明第二產業是當前12個海島縣的主導產業。第一產業的動態關聯度保持在0.5以上，略微有下降；第三產業與總產值的動態關聯度在起伏中遞增，表明第三產業發展態勢較好。三次產業的動態關聯度隨時段的變化越來越接近，表明三個產業發展趨于協調。

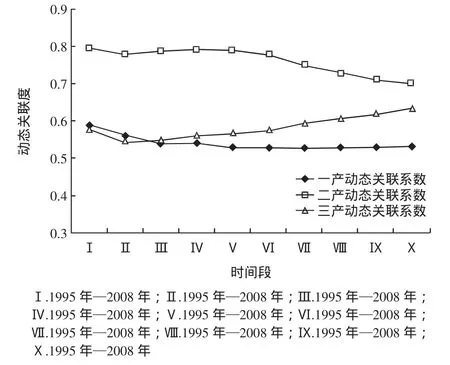
圖3 我國海島縣三次產業動態關聯變化圖Fig.3 Changes of the dynamic correlation of three industries in China′s island counties

2 產業結構變動程度和速度的測度

在分析產業結構變動狀況時，首先應判斷結構變動的程度。結構變動的程度，通常用結構變化值來衡量[2]。結構變化值的計算公式為：

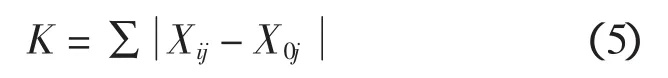
式中：K為區域產業結構變化值，Xij為研究末期i產業j的構成比例，X0j為研究基期0產業j的構成比例。

該結構變化值僅反映產業結構變動的總體程度，而不識別結構變動的方向，即既不涉及內部各產業比例的變動，也不涉及產業比例變動的增減，產業比例無論增還是減都包括在結構變動的范圍之內。

除了需要知道區域產業結構變動的總體程度，還需要知道其變動的速度。如果兩個或多個不同時段包括的時間長度相同，比如具有相同的年份數，通過比較各時段結構變化值的大小就可以直接判斷出各時段結構變化速度；但是如果兩個或多個不同時段包括的時間長度各不相同，則無法直接從結構變化值中判斷各時段結構變化的速度。這時，還需要另一個指標即“結構變化速度”來反映[2]。

結構變化速度的計算公式是：

式中：Ki為i時段產業結構變化值，Ni為i時段所包括的年份數，Si為i時段產業結構變化速度，可見結構變化速度實際上就是用序時平均法處理后的結構變化值的平均數。

2.1 海島縣產業結構變動及其與經濟增長的關系

根據地區生產總值，運用式（5）和式（6）計算得到12個海島縣及海島縣總計各個典型時段（1978年—2008年、1978年—1990年、1990年—2004年、1995年—2000年、2000年—2008年）的三次產業結構變化值和變化速度，在時段1978年—2008年，即改革開放以來的27年中，海島縣總計三次產業結構變化值達到60.7%，遠大于全國的平均水平（結構變化值為25.5%）；12個海島縣中變化值最高的玉環縣達77.12%、普陀區74.31%，最低的東山縣為20.43%；高于海島縣總計的有嵊泗、定海、洞頭等縣。

海島縣全部的變化速度為1.57%/a，玉環縣最高為2.49%/a，其次普陀達2.40%/a，東山縣最低為0.82%/a。變化速度在1.57%/a以上的有嵊泗、定海、玉環、洞頭等縣，其他則在1.57%/a以下。表2反映了改革開放以來各海島縣產業結構變化總體程度和速度的數量關系。

2.2 產業結構變動方向和強度的定量測度

在研究中，僅僅了解產業結構總體變動的程度和速度是遠遠不夠的，而且需要知道產業結構中，哪個產業收縮了，哪個產業擴張了，收縮和擴張的程度有多大，這就是產業結構變動的方向和強度問題。產業結構變動的方向和強度可以用結構變化趨勢值計量和表示[2]。結構變化趨勢值的計算公式是：

式中：X0j和Xij分別為研究期初0和期末i產業j的比重，Qj為產業j從期初0和期末i的變化趨勢值。Q等于1，表示產業比重沒有變化；Q大于1，表示產業比重上升和擴張；Q小于1，表示產業比重收縮或下降；Q值與1的差距越大，表示產業擴張或收縮的強度越大。

1978年—2008年期間，海島縣總的趨勢是三產擴張，二產、一產收縮，但存在兩種類型：一種是和總體情況一致；另一種是二產擴張，一、三產收縮，主要是崇明、嵊泗、岱山、東山和南澳等縣。但2005年—2008年三年中，各海島縣和整體有了一定變化，從各時段來看，由于1978年—2008年的時段較長，相應地各區域該時段的結構變化值也較大，2005年—2008年的時段較短，結構變化值也較小（表3）。

表2 我國海島縣產業結構變化值、變化速度和經濟增長速度Tab.2 Variation value and velocity of industrial structure and economic growth speed of China′s island counties

3 中國海島縣經濟實力的評估

每個海島縣經濟都有不同程度的增長，但由于海陸資源、生產水平和人文社會經濟條件等原因，海島縣域之間經濟發展存在著明顯的差異，在此對海島縣經濟綜合發展水平進行評估，從而進一步了解各海島縣經濟差異狀況[3，4]。

3.1 主成份分析方法

主成份分析是把原來多個變量轉化為少數幾個綜合指標，并盡可能多地保留原來較多變量所反映的信息，也是為了克服多指標變量之間信息重疊及人為確定指標權重的主觀性的一種統計方法，具有較強的全面性、綜合性和客觀性，是解決定性問題定量化的一種有效方法。因而在此用主成份分析法來確定海島經濟發展的實際水平。

3.2 指標體系建立與變量選取

影響海島縣經濟發展的因素是多方面的，既與自然條件有關，也與經濟發展水平、經濟結構和經濟規模等有關。為此根據海島縣經濟發展的特點，共選取4類22個指標：這些指標主要反映海島縣經濟發展、人均水平、產業結構、經濟實際生產特點和能力的指標。每類指標下設若干個變量。1993年、2002年、2008年三年取相同的變量，各年不同的數據，所選用的變量見表4。

3.3 方差分析

利用SPSS軟件進行計算，對原始數據進行標準化處理，以消除指標間的量綱，并建立相關系數矩陣（略）后，進行特征值提取。累計貢獻率說明主成份所包括的全部要素信息百分比。按特征值大于1的原則來考慮主成份，在此提取6個主成份，其累計方差貢獻率達到90%以上，因此可以認為反映了原來各要素所表示的主要特征。這就是經過數學變換，找出比原指標少的綜合指標，用來反映22項指標提供的全部信息的主要部分，已能反映原始變量的絕大部分信息。經過提取主成份后計算主成份載荷、主成份得分和得分權重，最后計算綜合實力水平。計算三年的特征值、貢獻率與累計貢獻率（表5）。

表3 海島縣三次產業結構變化趨勢值Tab.3 Trend value of three industries structure change in island counties

表4 變量選取Fig.4 Selection of variables

從1993年、2002年、2008年三年的方差分析表中可以看出，一般都要取6個主成分，累計貢獻率達到了90%左右，已能代表22個原始變量絕大部分信息。通過計算主成分載荷矩陣（見表6、表7、表8）。

3.4 綜合得分

計算主成分得分系數矩陣、主成分得分和綜合得分，現省略這幾步計算過程，只列出1993年、2002年和2008年三年的綜合得分對比表（表 9）。

從三年的綜合得分表的排序可以看出各海島縣綜合實力的變化情況，根據綜合得分繪制綜合得分柱狀圖（圖4）。

將1993年、2002年和2008年計算的主成分得分，以第1主成分得分為橫坐標，以第4主成分得分為縱坐標，繪制主成分得分圖（圖5a，b，c），從而反映產業結構的演變類型。

表5 方差分析（1993年、2002年、2008年）Tab.5 Variance analysis（1993， 2002， 2008）

表6 1993主成分載荷矩陣Tab.6 Principal component load matrix in 1993

表7 2002年主成分載荷矩陣Tab.7 Principal component load matrix in 2002

表8 2008年主成分載荷矩陣Tab.8 Principal component load matrix in 2008

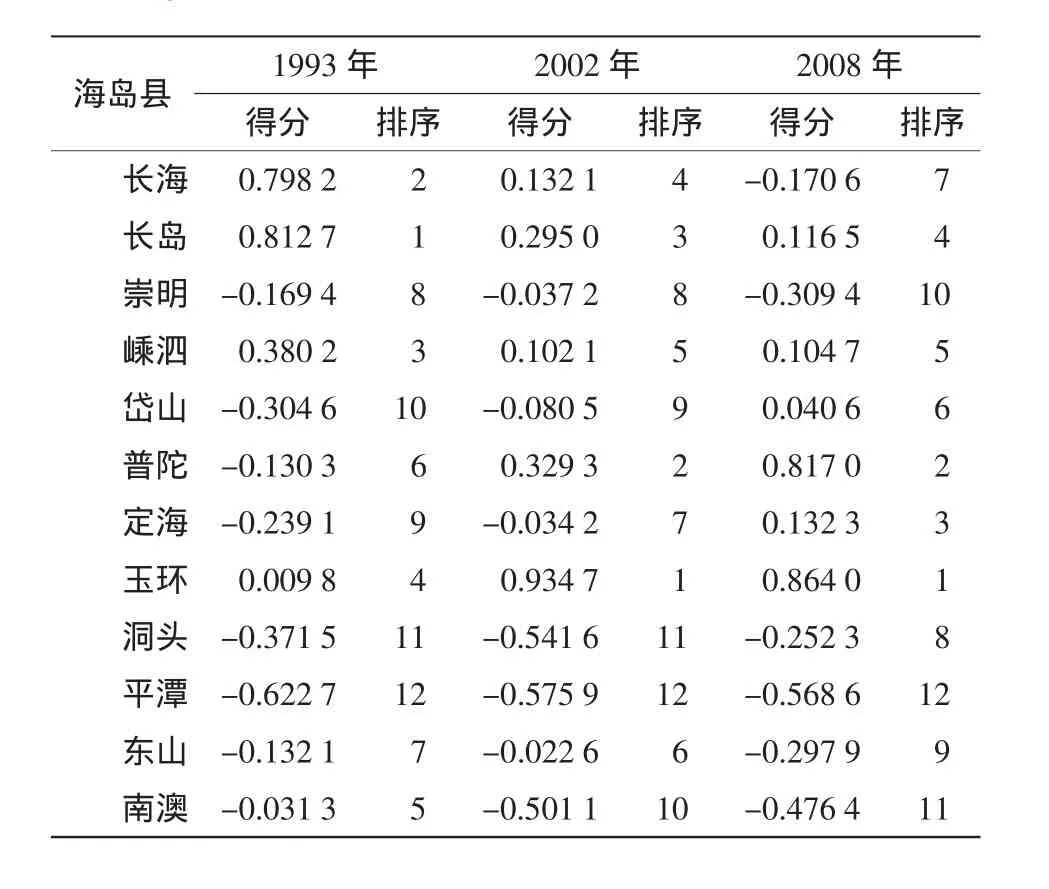
表9 1993年、2002年、2008年綜合得分對比表Tab.9 Contrast of comprehensive scores of economic strength of island counties in China（1993， 2002， 2008）

4 結 語

通過對海島縣經濟發展與產業結構分析，反映了不同年代的動態變化演變過程，既反映在時間的變化上，也反映在12個海島縣的空間動態變化上，而且隨著經濟發展的推移，各海島縣綜合實力也相應發生變化。其中除長海與長島二個海島縣仍以第一產業占主導地位外，其他海島縣趨向以第二、三產業為主的產業結構，從而使經濟綜合實力有了明顯的改變。

圖4 綜合得分圖Fig.4 Comprehensive scores of island counties

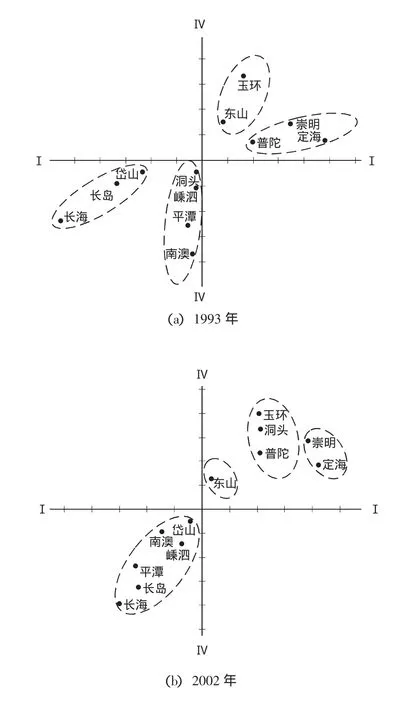
圖5 主成份得分圖Fig.5 Principal components scores of island countries

[1]張晉青，張耀光.灰色關聯度模型在海洋產業分析中的應用—以遼寧省為例[J].資源開發與市場，2010（2）：125-128.

[2]靖學青.經濟增長、結構變化與區域差異[M].上海：學林出版社，2008.

[3]張耀光，王國力，肇 博，等.中國海島縣際經濟差異與今后產業布局分析[J].自然資源學報，2005（2）：222-230.

[4]張耀光，劉 桓，張 巖，等.中國海島縣的經濟增長與綜合實力研究[J].資源科學，2008（1）：18-24.