自重作用下曲線連續剛構橋扭轉效應初探

王超,肖榮

(重慶市建筑科學研究院，重慶 400020)

0 引言

為了滿足路線線路需求或功能要求，曲線梁橋的修建越來越多[1]。但是由于曲線梁橋存在彎扭耦合作用，使其較之直線橋梁的受力和變形更加復雜，使得設計施工以及后期的檢測養護存在較大難度。本文以泥溪溝2號大橋為例，對其扭轉變形進行研究，總結曲線連續剛構橋的扭轉變形規律，以期為同類型的曲線連續剛構橋的施工監控提供參考。

1 工程概況

泥溪溝2號連續剛構大橋其孔跨布置為左線 （6×30+75.25＋140＋75.25＋2×30）m、 右線 （6×30+75.25＋140＋75.25＋3×30）m；主橋采用混凝土變截面預應力連續剛構箱梁，在橋跨方向上箱梁的跨中和根部梁高分別為3m、8.8m；頂板厚度（等厚度）為30cm，底板厚度從根部的100cm漸變到跨中的30cm，腹板厚度從根部至跨中分50cm、60cm、70cm三種厚度；箱梁頂板寬度為12.25m，其中翼緣懸臂長2.65m，底板寬度為6.95m；懸澆T構在縱向上被對稱劃分成16個節段；梁段數及梁段長從根部至跨中分別為8×3.5m、8×4.45m，邊跨和中跨合攏長度均為1.8m。[2]該大橋平面位于曲線半徑2000m的曲線上，其立面圖和平面圖如圖1所示。

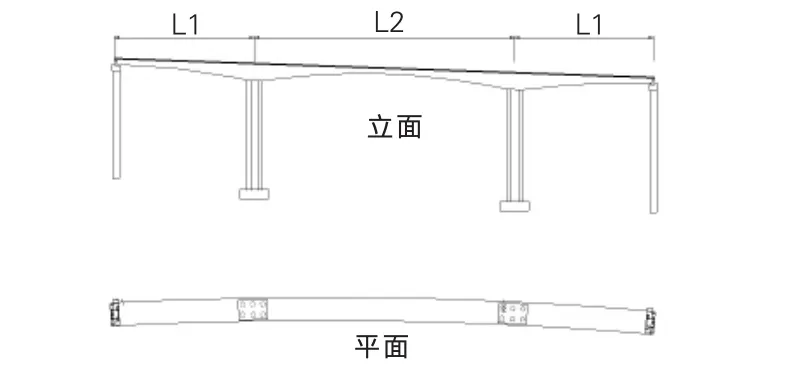
圖1 大橋設計圖

2 分析模型的建立

在保證截面及跨徑布置不變的前提下，分別建立了曲線半徑為200m、400m、800m、2500m的直線橋的有限元仿真模型，用以分析隨著曲率半徑的變化，對剛構橋扭轉效應的影響。論文中所涉及的模型上部結構和下部結構共被劃分成136個單元，其中88個單元為上部結構單元，48個單元為下部單元。當曲線半徑一定時（以200m曲線半徑為例），本文分析了墩高分別為60m、80m、120m三種情況時對結構的影響規律。采用Midas civil軟件計算時，橋梁所涉及的材料參數均按《公路鋼筋混凝土及預應力混凝土橋涵設計規范》JTGD62-2004[3]采用，材料的本構關系選取如圖2所示。

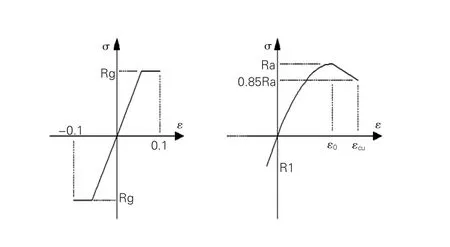
圖2 鋼筋及混凝土的應力-應變曲線圖

（1）混凝土本構關系如下表達：

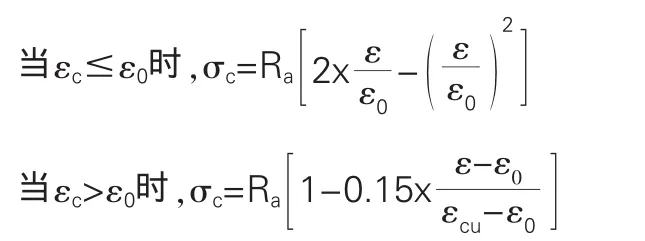
（2）鋼筋本構關系如下表達：

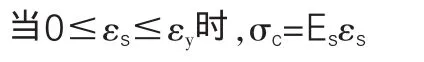
當εs>εy時，σs=Rg

式中:εc、εs、σc、σs為混凝土和鋼筋的應變、 應力， Es、Eg為混凝土和鋼筋的彈性模量，Ra為混凝土的標準強度,相當于σmax，ε0為相應于Ra時的混凝土壓應變，εcu為混凝土的極限壓應變。

3 連續剛構在自重作用下的計算結果及分析

無論在施工過程中還是成橋狀態，自重較之二期恒載和可變荷載對施工監控中的線形控制起到決定性的作用，故該文著重研究自重對該橋型扭轉效應的影響。借助對這一主要因素的研究，找出扭轉變形的控制截面以及曲線半徑與扭轉角的關系。為了方便敘述將模型中的各參數的含義表述如下。

文中扭轉角的含義為頂板翼緣板的內外兩側豎向位移的差值與梁寬的比值如圖3所示，即:tgθ=Δh/B；正負號代表的意義為：向曲線內側轉為正，向曲線外側轉為負[4]。

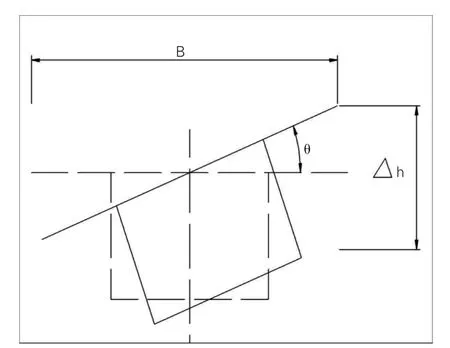
圖3 扭轉角示意圖

1節點和89節點分別是橋梁主梁端點，24節點和66節點分別是左右兩個橋墩的中心。

在自重作用下，曲線橋受彎扭效應影響，主梁不但產生豎向彎曲，而且在扭矩作用下產生主梁截面內的扭轉變形。圖4、圖5分別顯示了相同墩高、不同曲率及曲率相同、墩高不同時連續剛構橋的扭轉角沿橋縱向的變化。

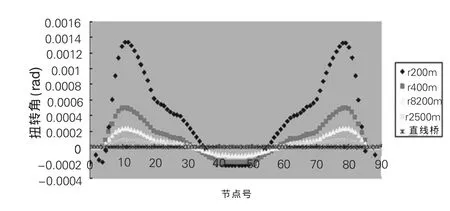
圖4 曲線半徑與扭轉角關系圖

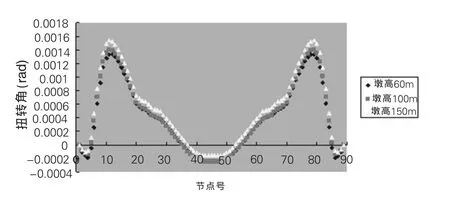
圖5 橋墩高度與扭轉角關系圖

3.1 中跨變形結果分析

墩高一定時，沿橋跨方向上扭轉角呈現一定的規律性。表現在梁體在扭矩作用下向曲線外側扭轉，同時中跨跨中附近主梁外邊緣豎向位移要大于內邊緣豎向位移，并且最大的扭轉角發生在中跨跨中截面。曲線半徑為200m的剛構橋與直線橋相比轉角為0.02o，內外側的高差為4.3mm，各曲線半徑橋梁中跨跨中截面的變形計算結果見表1。在施工監控線形控制時，應特別注意這一影響。

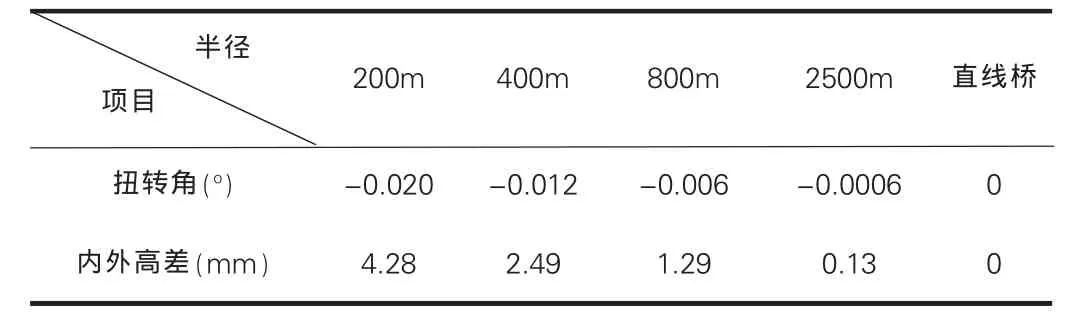
表1 中跨跨中截面扭轉角和內外高差

3.2 邊跨變形結果分析

墩高一定時，從距中跨跨中2/7L2到距邊跨端部1/8 L1截面處產生向曲線內側的扭轉。其中正扭轉角在邊跨跨中附近達到最大值。各曲線半徑橋梁邊跨跨中截面的變形計算結果見表2。值得提出，橋面越寬這一差值也越大，故當橋梁的寬度較大時應特別注意該截面扭轉所造成的內外高差的影響。當曲線半徑≥800m時，自重引起的邊跨跨中截面的內外高差≤3mm，并且變化速度很慢，因為自重這一控制因素對扭轉角影響甚微，而預應力在該截面處產生相反的扭轉角[4]，與自重扭轉角部分抵消。可以斷定當曲線半徑大于800m時，可按直線橋進行施工控制；當曲線半徑<800m時，應考慮曲率對橋面線形的影響，而且該種橋型的扭轉角控制截面為中跨跨中截面和邊跨跨中截面。

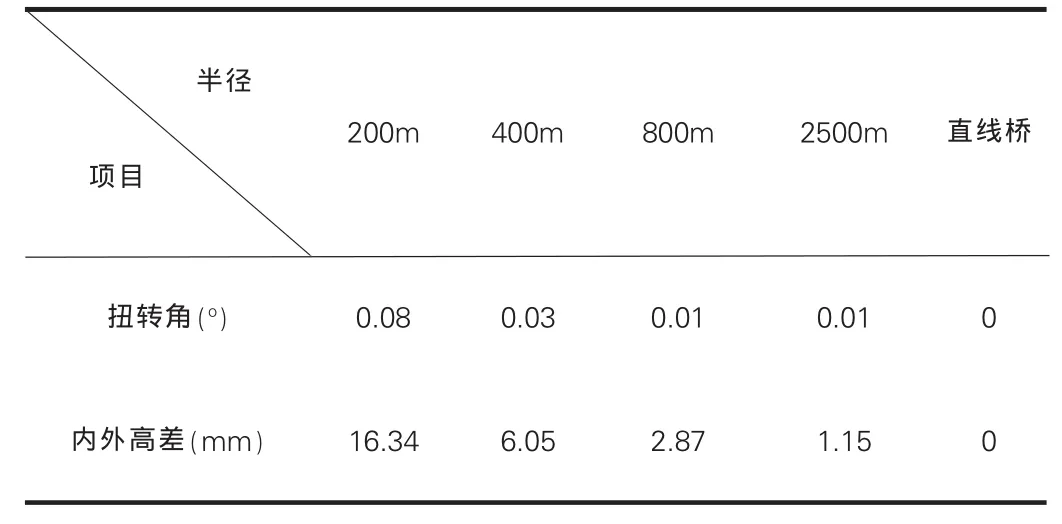
表2 邊跨跨中截面扭轉角和內外高差

3.3 墩高變化對變形結果影響分析

曲線半徑不變，隨著墩高的增加主梁中跨跨中的豎向位移逐漸增加。與此同時，該截面的扭轉角增大即內外緣高差也增大。計算結果顯示曲率半徑為200m時，墩高分別為60m、100m、150m的連續剛構橋，中跨跨中截面內外側的高差為2.1mm，詳見表3計算結果，與直線橋相比較可以忽略不計。

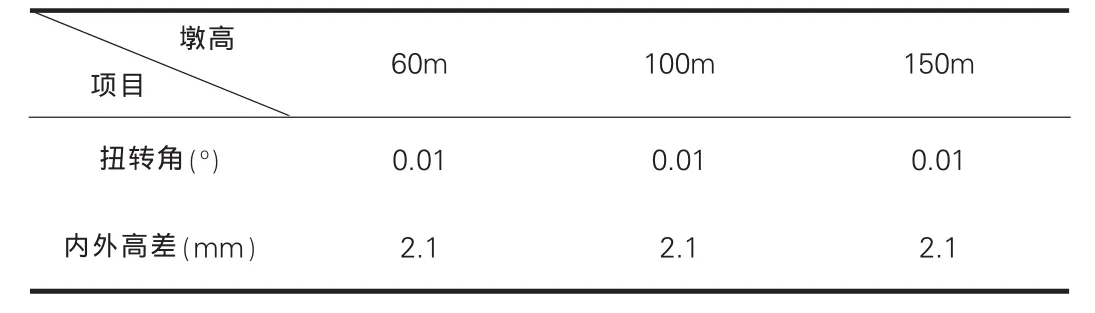
表3 曲線半徑200m中跨跨中截面扭轉角內外高差

4 結論

研究證明，該種橋型中跨跨中及邊跨跨中截面的扭轉角較大，故在泥溪溝2號大橋的線形控制中，將該兩個截面作為了控制截面，著重對該截面的扭轉角進行控制。大橋合攏后，實際測量證明，由于對控制截面的有效控制，橋面線形良好。

經分析，當曲線半徑≥800m時，曲線連續剛構橋在自重和預應力的相互作用下扭轉效應甚微，由于泥溪溝2號大橋的曲線半徑超過800m，故在其施工監控中按直線橋進行了變形計算，依次作為監控的基礎。

墩高的變化對連續剛構橋扭轉效應的影響不是很顯著。當曲線半徑一定、墩高在0~150m變化時，各個截面扭轉角基本一致，可以不考慮墩高變化對扭轉的影響。

[1]李莉，舒贛平.小曲率半徑曲線鋼箱梁橋設計研究[J].建筑結構，2011，41（增刊1）：244.

[2]孫廣華.曲線梁橋計算[M].北京：人民交通出版社，1994:64.

[3]JTGD62-2004公路鋼筋混凝土及預應力混凝土橋涵設計規范[S].北京：人民交通出版社，2004：10-13.

[4]王超.曲線連續剛構橋空間受力分析[D].重慶：重慶交通大學，2011:11-64.